
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
I. 2. 3 масса. Центр масс. Импульс. Закон сохранения импульса. ПлотностьСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Масса тела – физическая величина, являющаяся одной из основных характеристик материи, определяющая её инерционные (инертная масса) и гравитационные (гравитационная масса) свойства. Принято считать, что инертная и гравитационная массы равны друг другу (с точностью, не меньшей 10-12 их значения). В классической (ньютоновской) механике массой материальной точки называется положительная скалярная величина, являющаяся мерой инертности этой точки. Под действием силы материальная точка изменяет свою скорость не мгновенно, а постепенно, т.е. приобретает конечное по величине ускорение, которое тем меньше, чем больше масса материальной точки. Обычно массу тела определяют путём взвешивания на рычажных весах. В классической механике считается, что: § масса материальной точки не зависит от состояния движения точки, являясь её неизменной характеристикой; § масса – величина аддитивная, т.е. масса системы (например, тела) равна сумме масс всех материальных точек, входящих в состав этой системы; § масса замкнутой системы остаётся неизменной при любых процессах, происходящих в этой системе (закон сохранения массы). Эти положения ньютоновской механики подверглись пересмотру и уточнению в релятивистской механике. Центром масс (центром инерции) системы материальных точек называется точка С, радиус-вектор
где Импульсом
Импульс
Для замкнутой системы:
Формула (I.53) представляет собой закон сохранения импульса: импульс замкнутой системы сохраняется, т.е. не изменяется с течением времени. Закон сохранения импульса справедлив не только в классической физике, хотя он и получен как следствие законов Ньютона. Эксперименты доказывают, что он выполняется и для замкнутых систем микрочастиц (они подчиняются законам квантовой механики). Этот закон носит универсальный характер, т.е. закон сохранения импульса – фундаментальный закон природы.
Импульс системы равен произведению массы всей системы на скорость центра инерции:
Скорость центра инерции определяется следующим образом:
Плотностью
Если во всех точках тела плотность одинакова, то оно будет называться однородным. Масса однородного тела равна произведению его плотности на объём:
В случае неоднородного тела, его масса будет определена следующим образом:
где Средней плотностью
I.2.4 ВТОРОЙ ЗАКОН НЬЮТОНА
Основным законом динамики материальной точки является второй закон Ньютона, который говорит о том, как изменяется механическое движение материальной точки под действием приложенных к ней сил. Второй закон Ньютона: скорость изменения импульса
Под Векторная величина Можно дать и другую формулировку второго закона Ньютона: ускорение материальной точки совпадает по направлению с действующей на неё силой и равно отношению этой силы к массе материальной точки. Математически это можно представить так:
Тангенциальное и нормальное ускорения материальной точки определяются соответствующими составляющими силы
Сила Если на материальную точку одновременно действуют несколько сил:
Следовательно, каждая из сил, одновременно действующих на материальную точку, сообщает ей такое же ускорение, как если бы других сил не было (принцип независимости действия сил).
Дифференциальным уравнением движения материальной точки называется уравнение
В проекциях на оси прямоугольной декартовой системы координат это уравнение имеет вид:
где I.2.5 ТРЕТИЙ ЗАКОН НЬЮТОНА До сих пор мы говорили о силах, действующих на тело, рассматривая только одно это тело. Но не следует забывать о том, что сила не существует «сама по себе», а возникает при взаимодействии тел и является характеристикой (мерой) этого взаимодействия. Количественное описание механического взаимодействия тел было дано Ньютоном в его третьем законе динамики: действию всегда есть равное и противоположное противодействие, иначе, взаимодействия двух тел друг на друга между собой равны и направлены в противоположные стороны. Можно дать и более упрощённую формулировку третьего закона Ньютона: как бы ни происходило механическое взаимодействие между телами, тела эти не только взаимно действуют друг на друга, но действуют всегда с равными по величине и противоположно направленными силами. Третий закон, как и первые два, представляет собой обобщение огромного числа опытов и наблюдений, причём никогда не наблюдалось, какого бы то ни было исключения из этого общего для всех взаимодействий правила. Для удобства две силы, возникающие при взаимодействии двух тел, будем называть действием и противодействием. Тогда третий закон можно сформулировать следующим образом: действию всегда найдётся равное ему противодействие, иначе говоря, действия двух тел друг на друга всегда равны и противоположны по направлению. Следует отметить, что, так как действие (взаимодействие) распространяется с конечной скоростью, то существует запаздывание между действием и противодействием, т.е. противодействие возникает не мгновенно. Этот закон очевиден в статических случаях, когда взаимодействующие тела находятся в равновесии: например, давление тела, поставленного на пол, равно противодействию пола; действие груза, растягивающего пружину, равно противодействию внутренних сил упругости пружины. Силы противодействия часто называют силами реакции или просто реакциями. Сущность третьего закона заключается в идее о взаимодействии тел; оно даёт правило: если наблюдаем тело, подверженное действию какой-либо силы, то надо искать другое тело, которое является источником этой силы и к которому приложена сила противодействия. Итак, когда в механике речь идёт о силах, надо понимать, что мы имеем дело с механическим взаимодействием тел, и возникновение силы всегда есть результат действия или противодействия тел. Применительно, к материальным точкам третий закон Ньютона может быть сформулирован в виде: материальные точки попарно действуют друг на друга с силами, имеющими одинаковую природу, направленными вдоль одной прямой, соединяющей эти точки, равными по модулю и противоположными по направлению. Закон отражает принцип парного взаимодействия. То есть все силы в природе рождаются парами. Если
Третий закон Ньютона позволяет осуществить переход от динамики отдельной материальной точки к динамике системы материальных точек. Это следует из того, что и для системы материальных точек взаимодействие сводится к силам парного взаимодействия между материальными точками.
ГЛАВА I.3 РАБОТА И ЭНЕРГИЯ I.3.1 РАБОТА. МОЩНОСТЬ А. Работа постоянной силы. Работой
Формула (I.66) показывает, что работа является скалярной величиной и может иметь положительное или отрицательное значение в зависимости от знака косинуса угла а) б) в)
Работа, совершаемая силой Если рассмотреть элементарное перемещение Б. Работа переменной силы. Если сила не постоянна по величине, а является функцией перемещения, Элементарной работой
Тогда полная работа на пути от
Формула (I.68), показывает, что работа есть интеграл от силы по перемещению. Из этого утверждения следует, что площадь под кривой на графике зависимости
Единица работы в системе СИ называется джоулем (Дж). Джоуль равен работе, совершаемой силой 1Н при перемещении точки её приложения на 1м в направлении действия силы: 1 Дж = 1 Н·м. В. Работа против силы тяжести. Если тело равномерно поднимается, т.е. движется с постоянной скоростью в направлении, противоположном направлению действия силы тяжести, то над телом совершается работа, равная
где Г. Работа против сил трения (
Необходимо отметить, что работа против сил трения превращается в тепловую энергию (одна из форм энергии, связанная с движением атомов, молекул или других частиц, из которых состоит тело.), или говорят, что энергия, затрачиваемая на перемещение тела, диссипирует. Д. Работа, затрачиваемая на ускорение тела. Если под действием постоянной силы
где Если ускорение сообщается телу, находящемуся в состоянии покоя ( Обратите внимание: § совершённая над телом работа, запасается в форме кинетической энергии тела (подробнее см. в § I.3.3); § из формулы (I.71) видно, что работа, затрачиваемая на ускорение тела, не зависит от характера приложенной к телу силы. Поэтому действующая на тело сила не обязательно должна быть постоянной, а может зависеть от перемещения Е. Работа, затрачиваемая на упругую деформацию тела. Если пружина растягивается на длину Тогда формула для работы по деформации пружины примет вид:
Обратите внимание: § работа, затрачиваемая на деформацию (растяжение) пружины, запасается в виде потенциальной энергии растянутой пружины (подробнее см. в § I.3.3). Для характеристики скорости совершения работы, вводят понятие мощности. Различают среднюю и мгновенную мощности. Средней мощностью называется скалярная физическая величина, определяемая отношением работы, совершаемой силой или системой сил в течение конечного промежутка времени, к его продолжительности:
Мощностью (мгновенной мощностью) называется скалярная физическая величина, равная пределу, к которому стремится средняя мощность при бесконечном уменьшении промежутка времени:
Дадим другое определение мгновенной мощности. Мощностью (мгновенной мощностью) называется скалярная физическая величина, равная отношению элементарной работы
Если материальная точка или тело перемещается со скоростью
или
где Формула (I.77) показывает, что мощность, развиваемая под действием силы Другими словами, мощность – это работа за единицу времени. Единица мощности – ватт (Вт): 1 Вт – мощность, при которой за время 1с совершается работа в 1 Дж.
1 Вт = 1 Дж/с.
|
||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 580; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.177.45 (0.01 с.) |

 которой определяется выражением:
которой определяется выражением: , (I.50)
, (I.50) и
и 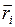 - масса и радиус-вектор i - й материальной точки,
- масса и радиус-вектор i - й материальной точки,  - общее число материальных точек в системе, а
- общее число материальных точек в системе, а  - масса всей системы. Центр масс является точкой, в которой может считаться сосредоточенной масса тела при его поступательном движении.
- масса всей системы. Центр масс является точкой, в которой может считаться сосредоточенной масса тела при его поступательном движении.
 й материальной точки называется векторная величина, равная произведению массы
й материальной точки называется векторная величина, равная произведению массы  её движения:
её движения: . (I.51)
. (I.51) системы, состоящей из
системы, состоящей из  . (I.52)
. (I.52) . (I.53)
. (I.53) . (I.54)
. (I.54) . (I.55)
. (I.55)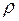 тела в данной точке М называется отношение массы
тела в данной точке М называется отношение массы 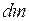 малого элемента тела, включающего точку М, к величине
малого элемента тела, включающего точку М, к величине  объёма этого элемента:
объёма этого элемента: (I.56)
(I.56)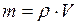 . (I.57)
. (I.57) , (I.58)
, (I.58) неоднородного тела называется отношение его массы к объёму:
неоднородного тела называется отношение его массы к объёму: . (I.59)
. (I.59) , т.е.
, т.е. . (I.60)
. (I.60) называется элементарным импульсом силы
называется элементарным импульсом силы  её действия.
её действия.
 . (I.61)
. (I.61) ;
;  . (I.62)
. (I.62) , сообщающая материальной точке нормальное ускорение, направлена к центру кривизны траектории точки и поэтому называется центростремительной силой.
, сообщающая материальной точке нормальное ускорение, направлена к центру кривизны траектории точки и поэтому называется центростремительной силой. ,
,  ,…,
,…,  . (I.63)
. (I.63) . (I.64)
. (I.64) ,
,  ,
,  , (I.65)
, (I.65) ,
,  и
и  - координаты движущейся точки.
- координаты движущейся точки.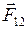 - сила, действующая на первую материальную точку со стороны второй, а
- сила, действующая на первую материальную точку со стороны второй, а 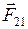 - сила, действующая на вторую материальную точку со стороны первой, то согласно третьему закону Ньютона,
- сила, действующая на вторую материальную точку со стороны первой, то согласно третьему закону Ньютона,  . Эти силы приложены к разным материальным точкам (телам), всегда действуют парами и являются силами одной природы.
. Эти силы приложены к разным материальным точкам (телам), всегда действуют парами и являются силами одной природы. постоянной силы
постоянной силы 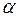 между векторами силы
между векторами силы  :
: . (I.66)
. (I.66)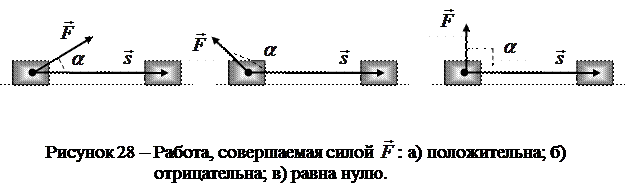
 работа силы
работа силы  , то силу
, то силу  , и направлена под углом
, и направлена под углом  силы
силы  материальной точки называется скалярная физическая величина, равная
материальной точки называется скалярная физическая величина, равная . (I.67)
. (I.67) до
до 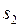 находится как:
находится как: . (I.68)
. (I.68)
 , (I.69)
, (I.69) - работа по поднятию тела;
- работа по поднятию тела; 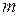 - масса тела;
- масса тела;  м/с2 – ускорение свободного падения;
м/с2 – ускорение свободного падения;  - высота, на которую поднимается тело, т.е. перемещение.
- высота, на которую поднимается тело, т.е. перемещение. ). Если тело движется с постоянной скоростью (равномерно) против сил трения, то, над ним совершается работа. При этом сила
). Если тело движется с постоянной скоростью (равномерно) против сил трения, то, над ним совершается работа. При этом сила 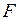 совпадает по направлению с перемещением
совпадает по направлению с перемещением  и равна по величине силе трения
и равна по величине силе трения  .
. . (I.70)
. (I.70)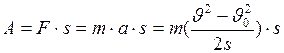 . Следовательно,
. Следовательно, , (I.71)
, (I.71) - скорость, которую достигает тело;
- скорость, которую достигает тело;  - ускорение.
- ускорение. ), то формула (I.70), примет вид:
), то формула (I.70), примет вид:  . Другими словами, работа, затрачиваемая на ускорение тела равна изменению его кинетической энергии.
. Другими словами, работа, затрачиваемая на ускорение тела равна изменению его кинетической энергии. .
. до
до  . Тогда в формулу для работы
. Тогда в формулу для работы  следует подставить среднее значение силы
следует подставить среднее значение силы 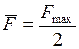 . Введём обозначения:
. Введём обозначения: 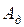 - работа против упругой силы, работа по деформации пружины;
- работа против упругой силы, работа по деформации пружины;  - жёсткость пружины;
- жёсткость пружины;  - растяжение пружины.
- растяжение пружины. . (I.72)
. (I.72) . (I.73)
. (I.73) . (I.74)
. (I.74) к малому интервалу времени
к малому интервалу времени  . (I.75)
. (I.75) , (I.76)
, (I.76) , (I.77)
, (I.77) .
.


