
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
I. 1. 2 вектор перемещения. ПутьСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При движении точки положение её радиус-вектора в пространстве изменяется. Приращение радиус-вектора, характеризующего конечное и начальное положения точки, движущейся в течение некоторого промежутка времени
Векторы перемещений складываются геометрически, по правилу параллелограмма или многоугольника (правило сложения векторов) (см. приложение 1). Путь ( Пример: Материальная точка последовательно перемещается из положения
Путь, пройденный материальной точкой, будет равен сумме длин участков траектории:
Вектор перемещения
При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и модуль перемещения
I.1.3 СКОРОСТЬ. УСКОРЕНИЕ. Для характеристики быстроты движения тел в механике вводится понятие скорости. Различают: среднюю и мгновенную скорости. Средней скоростью за промежуток времени
Средняя скорость характеризует движение в течение всего того промежутка времени, для которого она определена. Направление вектора средней скорости совпадает с направлением приращения радиус-вектора, т.е. направлен вдоль хорды, стягивающей соответствующий участок траектории точки (рис. 4 и 6). Мгновенной скоростью (скоростью), называется физическая величина, равная пределу, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени
Мгновенная скорость является первой производной по времени от радиус-вектора рассматриваемой точки:
Вектор мгновенной скорости материальной точки направлен по касательной к траектории в сторону движения (рис. 6).
Для характеристики быстроты изменения скорости точки в механике вводится понятие ускорения. Средним ускорением называется физическая величина, равная отношению изменения скорости материальной точки к длительности промежутка времени
Направление векторов
Мгновенным ускорением (ускорением) материальной точки в момент времени
Мгновенное ускорение является первой производной по времени скорости рассматриваемой точки, или второй производной по времени от радиус-вектора этой точки:
Вектор ускорения точки можно разложить на две составляющие: тангенциальную Тангенциальная составляющая вектора ускорения направлена вдоль касательной к траектории в данной точке и называется тангенциальным (касательным) ускорением:
Тангенциальное ускорение характеризует изменение вектора скорости по модулю. Вектор Нормальная составляющая вектора ускорения, направлена по нормали к траектории к центру её кривизны в данной точке и называется нормальным (центростремительным) ускорением:
Нормальное ускорение характеризует изменение вектора скорости по направлению при криволинейном движении. Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих (рис.8):
В зависимости от тангенциальной и нормальной составляющих ускорения, движение будет подразделяться на несколько видов (таблица 1.):
Таблица 1. Классификация движения в зависимости от составляющих ускорения: тангенциального (
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 522; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.252.215 (0.012 с.) |

 , называется вектором перемещения (перемещением)
, называется вектором перемещения (перемещением)  (
( ). Вектор перемещения направлен вдоль хорды траектории точки (рис.4).
). Вектор перемещения направлен вдоль хорды траектории точки (рис.4).
 или
или  ) (рис.4) - скалярная величина (скалярная функция времени:
) (рис.4) - скалярная величина (скалярная функция времени:  ), равная длине участка траектории, пройденного движущейся точкой за данный промежуток времени. Пути, пройденные точкой за последовательные промежутки времени, складываются алгебраически.
), равная длине участка траектории, пройденного движущейся точкой за данный промежуток времени. Пути, пройденные точкой за последовательные промежутки времени, складываются алгебраически. в положение
в положение  , затем в
, затем в  ,
,  и т.д. (рис. 5).
и т.д. (рис. 5).
 .
. соединяет начальное положение точки с её конечным положением. В рассмотренном примере модуль вектора перемещения
соединяет начальное положение точки с её конечным положением. В рассмотренном примере модуль вектора перемещения  не равен пути
не равен пути  равен пройденному пути
равен пройденному пути  . (I.3)
. (I.3) . (I.4)
. (I.4) . (I.5)
. (I.5)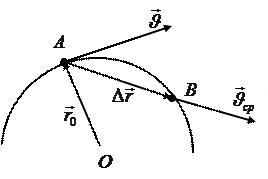
 . (I.6)
. (I.6) и
и 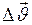 совпадают (рис.7).
совпадают (рис.7).
 называется физическая величина, равная пределу, к которому стремится среднее ускорение при бесконечном уменьшении промежутка времени
называется физическая величина, равная пределу, к которому стремится среднее ускорение при бесконечном уменьшении промежутка времени 
 . (I.7)
. (I.7) . (I.8)
. (I.8) и нормальную
и нормальную  .
. . (I.9)
. (I.9)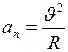 . (1.10)
. (1.10) . (I.11)
. (I.11)
 0
0



