
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейная зависимость векторов.Содержание книги
Поиск на нашем сайте
Пусть дана система векторов
и α1, α2,...αn - действительные числа. Тогда векторы вида
называются линeйнoй комбинaциeй вeктоpов cиcтeмы (1). Определение. Система векторов (1) называется линейно зависимой, если существует такая линейная комбинация этих векторов, равная нулевому вектору, т.е.
и хотя бы одно из чисел Определение. Система (1) называется линейно независимой, если равенство (2) возможно тогда и только тогда, когда все числа αi=0. Определение. Если какой-либо вектор
то говорят, что вектор Теорема. Для того чтобы векторы системы (1) были линейно зависимы (n>1), необходимо и достаточно, чтобы по крайней мере один из них линейно выражался через остальные. Следствие. Если векторы системы (1) линейно независимы, то ни один из них нельзя линейно выразить через остальные. В частности, ни один из них не может быть нулевым.
Теорема. Для того чтобы два вектора были линейно зависимы, необходимо и достаточно, чтобы они были коллинеарны. Следствие. Два вектора линейно независимы тогда и только тогда, когда они неколлинеарны.
Теорема. Любой вектор
причем это разложение единственно. Теорема. Для того чтобы три вектора были линейно зависимы, необходимо и достаточно, чтобы они были компланарны. Следствие. Три вектора линейно независимо тогда и только тогда, когда они некомпланарны.
Теорема. Любой вектор
причем это разложение единственно. Tеорема. Любые четыре вектора линейно зависимы.
Определение. Говорят, что два лежащих в плоскости α линейно независимых вектора Итак: 1) любая пара лежащих в данной плоскости неколлинеарнах векторов образует базис на этой плоскости; 2) любая тройка некомпланарных векторов образует базис в пространстве.
Координаты на прямой. Прямая l, на которой задана точка 0, называемая началомкоординат, задан единичный вектор Пусть М - произвольная точка прямой. Тогда вектор
линеарен вектору Так как Обратно, для каждого действительного числа х найдется единственная точка М оси l, координата которой равна х. Таким образом, положение любой точки координатной оси однозначно определяется заданием координаты этой точки.
Координаты на плоскости.
Пусть на плоскости α заданы две координатные оси ОХ и OY с неколлинеарными ортами Точка 0 называется началом кооpдинат, векторы
Числа х и у называются афинными координатами точки М в системе (0, (записывается: М(х,у)). Вектор Афинная система координат (0, Теорема. Пусть
Тогда Следствие 1. Пусть даны точки А (х 1, y 1) и В (х 2, у 2). Тогда
Следствие 2. Два вектора
Афинная система координат (0, Координаты в пространстве.
Определение. Пусть в пространстве заданы три координатные оси OX, OY и OZ с некомпланарными ортами Точка 0 - начало координат, векторы Так как векторы любого вектора
Числа x, y, z называются координатами точки М (записывается: М (х, у, z)), Афинную систему часто обозначают через OXYZ. Оси OX, OY, OZ называют соответственно осями абсцисс, ординат и аппликат. Плоскости, определяемые координатными осями, т.е. OXY, OYZ, OXZ, называют координатными плоскостями. Эти плоскости делят все пространство на восемь частей, называемых координатными октантами. Если упорядоченная тройка векторов В частности, если даны точки А (х 1, у 1, z 1), В (х 2, у 2, z 2), то
Векторы
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 632; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.009 с.) |

 (1)
(1)
 (2)
(2) .
.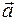 можно представить в виде линейной комбинации векторов системы (1), т.е.
можно представить в виде линейной комбинации векторов системы (1), т.е. и
и 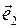 этой плоскости, т.е. представить в виде:
этой плоскости, т.е. представить в виде:
 , т.е. представить в виде:
, т.е. представить в виде:
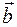 (любые три линейно независимых вектора
(любые три линейно независимых вектора  ) образуют на этой плоскости (в пространстве) базис, если любой вектор, лежащий в этой плоскости α (любой вектор пространства), может быть представлен в виде линейной комбинации векторов
) образуют на этой плоскости (в пространстве) базис, если любой вектор, лежащий в этой плоскости α (любой вектор пространства), может быть представлен в виде линейной комбинации векторов  , называемый ортом, называется координатнойосью.
, называемый ортом, называется координатнойосью.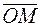 кол-
кол- . Вектор
. Вектор 
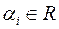


 .
.
 .
.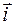 и
и 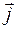 .
. имеет место разложение:
имеет место разложение: .
.




