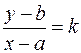Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Скалярное произведение векторов в координатной форме.Содержание книги
Поиск на нашем сайте
Пусть в прямоугольной системе координат заданы векторы:
В частности
Если даны точки А(х1,у1,z1) и В(х2,у2,z2), то, как известно,
-формула расстояния между двумя точками.
Так как
и
х 1 x 2 + y 1 y 2 + z 1 z 2 = 0.
Определители второго и третьего порядков
Определение. Таблица, составленная из чисел, записанных в следующем виде:
называется квадратной матрицей n-го порядка или просто матрицей n-го порядка. Первый индекс i элемента а ij матрицы А указывает на номер строки, а второй индекс j - на номер столбца, на пересечении которых стоит элемент аij.
Пусть дана квадратная матрица А второго порядка:
Определителем (детерминантом) матрицы А второго порядка называется число Δ равное:
Для матрицы А третьего порядка, где
ее определитель Δ есть число, которое вычисляется следующим образом: Δ = а 11 а 22 а 33 + а 12 а 23 а 31 + а 13 а 21 а 32 – а 13 а 22 а 31 – а 11 а 23 а 32 – а 12 а 21 а 33.
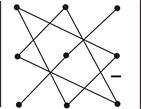
Чтобы запомнить, какие произведения в правой части равенства берутся со знаком "+", а какие со знаком "–", полезно использовать следующее правило треугольников:
Легко проверить, что
- разложение определителя по элементам первой строки.
Векторное произведение векторов в координатной форме.
Пусть в прямоугольной системе координат заданы векторы
Последнее равенство можно записать так:
Итак,
Тогда
Смешанное произведение векторов в координатной форме.
Пусть в прямоугольной системе координат заданы векторы
Отсюда следует, что векторы
Полярные координаты.
Возьмем на плоскости произвольную точку 0, которую назовем полюсом, и ось ОР, задаваемую единичным вектором Величины r и φ называются полярными координатами точки М, r- полярный радиус, φ- полярный угол. При этом считаем, что полярные координаты точек плоскости изменяются в следующих пределах: С прямоугольными координатами полярные связаны следующими соотношениями: х = r cosφ, у = r sinφ.
Так как х 2 + у 2 = r 2, то
Прямоугольные координаты на плоскости.
x = x 'cosφ - y 'sinφ + α, y = x 'sinφ + y 'cosφ + β
В частности, если
x = х ' + α, у = у ' + β - формулу преобразования координат при параллельном переносе системы координат Если же точки 0 и 0' совпадают, то x = x 'cosφ - y 'sinφ, y = x 'sinφ + y 'cosφ.
- формулы преобразования координат при повороте системы координат вокруг начала на угол φ
ПРЯМАЯ НА ПЛОСКОСТИ.
Прямая на плоскости
следует, что
- угловой коэффициент относительно выбранной системы координат. В частности, для прямоугольной системы координат (0, k = tgα, где α – угол между осью ОХ и любым направляющим вектором прямой l. Угол α называется углом наклона прямой l к оси ОХ.
Если прямая l параллельна оси ОY, то l пересекает ось OХ в некоторой точке Р(а,0). Тогда все точки прямой и только они удовлетворяют соотношению x = a - уравнение прямой, проходящей через точку параллельно оси ОУ. Заметим, что в качестве направляющего вектора такой прямой можно взять вектор Пусть прямая l проходит через точку A (а, b) и имеет угловой коэффициент k. Возьмем произвольную точку М (х, у) на прямой l. Тогда Следовательно,
Отсюда y – b = k (x - а) -уравнение прямой с угловым коэффициентом k.
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 380; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.178.220 (0.006 с.) |

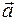 = (х1,у1,z1),
= (х1,у1,z1), 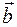 = (х2,у2,z2). Тогда
= (х2,у2,z2). Тогда
 =(x2-х1,y2-у1,z2-z1) и значит.
=(x2-х1,y2-у1,z2-z1) и значит.
 , то
, то
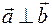 тогда и только тогда, когда выполняется равенство:
тогда и только тогда, когда выполняется равенство:




 =
= 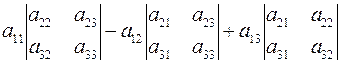

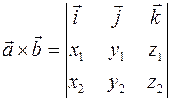


 = (x 3, y 3, z 3). Тогда
= (x 3, y 3, z 3). Тогда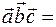


 , которую назовем полярной осью. Тогда положение произвольной точки М плоскости можно определить двумя числами: r -длина отрезка ОМ и φ - угол, который образует отрезок ОМ с осью ОР в положительном направлении, т.е. при движении против часовой стрелки.
, которую назовем полярной осью. Тогда положение произвольной точки М плоскости можно определить двумя числами: r -длина отрезка ОМ и φ - угол, который образует отрезок ОМ с осью ОР в положительном направлении, т.е. при движении против часовой стрелки. . Таким образом, получаем систему координат, которая называется полярной системой координат.
. Таким образом, получаем систему координат, которая называется полярной системой координат.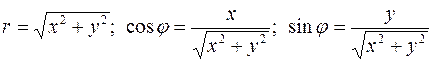
 Пусть дана старая и новая прямоугольные системы координат, соответственно (0,
Пусть дана старая и новая прямоугольные системы координат, соответственно (0, 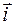 ,
, 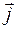 ) и (О',
) и (О', 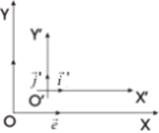

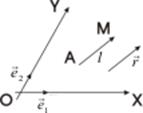 Пусть в плоскости α задана афинная система координат (0,
Пусть в плоскости α задана афинная система координат (0,  ,
, 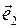 ) и прямая l, принадлежащая этой плоскости α. Составим уравнение прямой l. Заметим, что положение прямой l однозначно определено, если известен вектор, коллинеарный этой прямой и называемый направляющим вектором прямой, и точка, через которую прямая проходит. Очевидно, что в качестве направляющего вектора прямой можно взять любой вектор, коллинеарный данной прямой. Пусть
) и прямая l, принадлежащая этой плоскости α. Составим уравнение прямой l. Заметим, что положение прямой l однозначно определено, если известен вектор, коллинеарный этой прямой и называемый направляющим вектором прямой, и точка, через которую прямая проходит. Очевидно, что в качестве направляющего вектора прямой можно взять любой вектор, коллинеарный данной прямой. Пусть  = (m1,n1) и
= (m1,n1) и 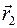 =(m2,n2) - какие-либо направляющие векторы прямой l. Тогда из необходимого и достаточного условия коллинеарности двух векторов
=(m2,n2) - какие-либо направляющие векторы прямой l. Тогда из необходимого и достаточного условия коллинеарности двух векторов Если прямая l не параллельна оси OY, то
Если прямая l не параллельна оси OY, то  следовательно,
следовательно,
 )
)

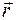 (0,р), где р - произвольное отличное от нуля число. В этом случае, как видим угловой коэффициент прямой не существует.
(0,р), где р - произвольное отличное от нуля число. В этом случае, как видим угловой коэффициент прямой не существует. =(х - а, у - b) - направляющий вектор прямой l.
=(х - а, у - b) - направляющий вектор прямой l.