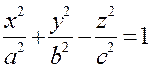Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основная теорема о поверхностях второго порядкаСодержание книги
Поиск на нашем сайте
Определение. Поверхностью второго порядка (ПВП) называется множество всех точек пространства, которые в прямоугольной системе координат удовлетворяют уравнению:
Теорема. Для любой поверхности второго порядка существует прямоугольная система координат OXYZ, в которой уравнение(1) имеет один из следующих 17 видов:
1) эллипсоид:
2 ) мнимый эллипсоид:
3) однополостный гиперболоид:
4) двуполостный гиперболоид:
5) конус:
6) мнимый конус:
7) эллиптический параболоид: z= а х2+ b y2 (а,b >О);
8) гиперболический параболоид: z= - ax2+by2 (а,b >0);
9 ) эллиптический цилиндр:
10) мнимый эллиптический цилиндр:
11) гиперболический цилиндр:
12) параболический цилиндр: у2=2рх;
13) пара пересекающихся плоскостей:
14) пара мнимых пересекающихся плоскостей:
15 ) пара параллельных плоскостей: у2= а 2(а
16) пара мнимых параллельных плоскостей: у2+ а2 =0 (а
17) пара совпадающих плоскостей: у2=0.
Уравнения 1) - 17) называются каноническими уравнениями поверхностей второго порядка. Выделим некоторые общие типы поверхностей второго порядка.
Цилиндрические поверхности
Определение. Цилиндрической поверхностью называется множество параллельных прямых (образующих), проходящих через все точки некоторой линии, называемой направляющей.
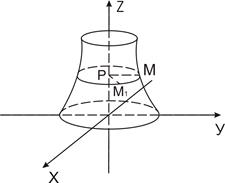
Пусть цилиндрическая поверхность задана таким образом в прямоугольной системе координат OXYZ, что образующие этой поверхности параллельны оси OZ, а направляющая лежит в плоскости OXY и задается уравнением:
F(x,у) =0
Если взять произвольную точку M(z,y,z) на цилиндрической поверхности, то ее проекция на плоскость OXY есть точка M1(х1,у1,0). Так как точки M и М1 лежат на образующей, то х1=х, у1=у. А так как точка М1 лежит на направляющей, то координаты точки М1, а, значит, и точки M, удовлетворяют уравнению F(x,у)=0.
Итак, уравнению удовлетворяют координаты любой точки цилиндрической поверхности. Следовательно, уравнение
F(x,у)=0
– искомое уравнение цилиндрической поверхности.
Если в прямоугольной системе координат OXYZ направляющая является кривой второго порядка, задаваемой каноническим уравнением вида F(x,у)=0, а образующие параллельны оси OZ, то цилиндрическими поверхностями второго порядка будут:
1) х2+y2=z2 — прямой круговой цилиндр;
2)
3)
4) у2=2рх - параболический цилиндр.
Заметим, что характерной чертой уравнения рассматриваемых цилиндрических поверхностей, является отсутствие в этих уравнениях одной из переменных.
Конические поверхности Определение. Конической поверхностью называется множество прямых (образующих), проходящих через некоторую точку (вершину) и пересекающих некоторую линию (направляющую).
Коническая ПВП — коническая поверхность с направляющей, являющейся КВП.
Если вершина совпадает с началом прямоугольной системы координат OXY, а направляющей служит эллипс:
То уравнение конической поверхности имеет вид:
– уравнение конической поверхности
Поверхности вращения Определение. Поверхность называется поверхностью вращения, если она вместе с каждой своей точкой содержит и всю окружность, полученную вращением этой точки вокруг некоторой фиксированной прямой, называемой осью вращении. Пусть на плоскости YOZ задана кривая линия l уравнением вида F(y,z)=0
Тогда уравнение поверхности вращения, образованной вращением кривой l вокруг оси OZ имеет вид:
Эллипсоид
Гиперболоид.
Однополостный гиперболоид:

Каноническое уравнение двухполоcного гиперболоида имеет вид:
Параболоид
Эллиптический параболоид.
z=ах2+by2 (а,b>0).
Гиперболический параболоид.
z=-ax2+by2 (a,b>0)
Литература: 1. Александров П.С. Курс аналитической геометрии и линейной алгебры. – М: Наука, 1979. 2. Биркгоф Г., Барти Т. Современная прикладная алгебра. – М.: Мир, 1976. 3. Бузланов А.В., Монахов В.С. Лабораторные работы по курсу «Алгебра и теория чисел». – Гомель: Ротапринт ГГУ им. Ф. Скорины, 1991. 4. Бузланов А.В., Каморников С.Ф., Кармазин А.П. Лабораторные работы по курсу «Алгебра и теория чисел» (раздел «Линейная алгебра») для студентов математического факультета. Часть I, II, III. – Гомель: Ротапринт ГГУ им. Ф. Скорины, 1990, 1991. 5. Бурдун А.А., Мурашко Е.А., Толкачёв М.М., Феденко А.О. Сборник задач по алгебре и аналитической геометрии. – Мн.: Университетское, 1989. 6. Ильин В.А., Позняк Э.Г. Аналитическая геометрия. – М.: Наука, 1982. 7. Ильин В.А., Позняк Э.Г. Линейная алгебра. – М.: Наука, 1974. 8. Курош А.Г. Курс высшей алгебры. – М.: Наука, 1968. 9. Милованов М.В., Тышкевич Р.И., Феденко А.С. Алгебра и аналитическая геометрия. Часть I, II. – Мн.: Вышэйшая школа, 1984, 1987. 10. Рублёв А.Н. Курс линейной алгебры и аналитической геометрии. – М.: Вышэйшая школа, 1972.
Учебное издание
ХОДАЛЕВИЧ АЛЕКСАНДР ДМИТРИЕВИЧ БОРОДИЧ РУСЛАН ВИКТОРОВИЧ РЫЖИК ВАЛЕНТИНА НИКОЛАЕВНА
«Аналитическая геометрия» Тексты лекций
Подписано в печать __.__.__. Формат 60x84 1/16. Бумага писчая № 1 Печать офсетная. Гарнитура Таймс. Усл. П. Л. 4,7. Уч.-изд.л. 3,72. Тираж ___ экз.
Учреждение образования «Гомельский государственный университет имени Франциска Скорины» 246019, г. Гомель, ул. Советская, 104
Отпечатано на полиграфической технике с оригинала-макета учреждения образования «Гомельский государственный университет имени Франциска Скорины» 246019, г. Гомель, ул. Советская, 104
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 374; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.78.215 (0.008 с.) |


 (1)
(1)
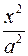 +
+ 
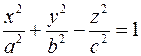








 0)
0)