
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные операции над векторами.Стр 1 из 8Следующая ⇒
А.Д. Ходалевич Р.В. Бородич В.Н. Рыжик «Аналитическая геометрия» Тексты лекций Гомель, 2004 УДК 514 (078) ББК 22.151 Я73 Х 69
Рецензенты: Семенчук В.Н. – профессор, доктор физико-математических наук кафедра высшей математики учреждения образования «Гомельский государственный университет имени Франциска Скорины».
Рекомендован к изданию научно-методическим советом учреждения образования «Гомельский государственный университет имени Франциска Скорины» 24 марта 2004 года, протокол № 7
Ходалевич А.Д. Х 69 Аналитическая геометрия: Тексты лекций. /А.Д.Ходалевич, Р.В.Бородич, В.Н. Рыжик. − Гомель: УО «ГГУ им. Ф.Скорины»; 2004 − 65с.
Дается краткое изложение курса лекций по аналитической геометрии для студентов, обучающихся по специальности «Прикладная математика»
УДК 514 (078) ББК 22.151 Я73 Х 69
© А.Д. Ходалевич, Р.В. Бородич, В.Н. Рыжик, 2004 © Учреждение образования «Гомельский государственный университет имени Франциска Скорины», 2004
СОДЕРЖАНИЕ
1. Векторы и координаты………………………………….…4 2. Прямая на плоскости………………………………………20 3. Плоскость…………………………………………………...25 4. Прямая в пространстве. Взаимное расположение прямой и плоскости в пространстве…………………………29 5. Кривые второго порядка…………………………………...33 6. Поверхности второго порядка……………………………..56
Литература………………………………………………….….64
Аналитическая геометрия - это раздел математики, в котором геометрические объекты изучаются с помощью алгебраических методов, в основе которых лежит понятие координат. ВЕКТОРЫ И КООРДИНАТЫ Понятие вектора Пусть А – произвольное непустое множество. Декартовым кваратом А называется множество A 2 = Бинарным отношением на А называется любое подмножество Отношением эквивалентности на А называется такое бинарное отношение 1) 2) если ( 3) если (
Теорема. Любое отношение эквивалентности на множестве А определяет разбиение этого множества на попарно непересекающиеся классы (классы эквивалентности). Обратно, любое разбиение множества А на попарно непересекающиеся классы определяет отношение эквивалентности на А.
Направленный отрезок – отрезок, у которого указано, какая точка является началом, а какая концом. Обозначается Пусть заданы направленные отрезки Если направленные отрезки Абсолютной величиной или модулем (длиной) направленного отрезка Два направленных отрезка
Теорема. Отношение равенства направленных отрезков является отношением эквивалентности.
Тогда вектором называется абстрактный объект, совпадающий с некоторым классом эквивалентности. Таким образом, каждый из равных друг другу направленных отрезков считается представлением (изображением) данного вектора, а неравные направленные отрезки считаются представлением разных векторов. Поэтому в дальнейшем вектор изображается точно так, как и соответствующий ему направленный отрезок.
Векторы Три и более векторов называются компланарными, если образующие их направленные отрезки параллельны некоторой плоскости. Нулевым вектором называется вектор, начало которого совпадает с его концом (обозначается
Проекции.
Назовем осью прямую, на которой указано направление, которое будем называть положительным.
Пусть l - некоторая ось, α - плоскость, непараллельная оси l. Через произвольную точку А пространства проведем плоскость α'||α и обозначим точку пересечения плоскости α' c осью l через А1. Тогда точка А1 называется проекцией точки А на ось l относительно плоскости α. В частности, если α
Пусть теперь задан вектор Тогда вектор а) | б) - | Обычно из контекста ясно о проекции относительно какой плоскости идет речь. Поэтому величину проекции вектора
Если прямая l Определение. Углом между двумя векторами, или между осями, или между вектором и осью называется наименьший угол α, на который надо повернуть один из векторов или одну из осей до совпадения по направлению с другим вектором или осью. Из определения следует, что 0
Теорема. Проекция вектора на ось обладает следуицики свойствами: 1) 2) 3)
1) 2)
Определение. Векторным произведением двух векторов 1) | 2) 3) векторы
Координаты на прямой. Прямая l, на которой задана точка 0, называемая началомкоординат, задан единичный вектор Пусть М - произвольная точка прямой. Тогда вектор
линеарен вектору Так как Обратно, для каждого действительного числа х найдется единственная точка М оси l, координата которой равна х. Таким образом, положение любой точки координатной оси однозначно определяется заданием координаты этой точки.
Координаты на плоскости.
Пусть на плоскости α заданы две координатные оси ОХ и OY с неколлинеарными ортами Точка 0 называется началом кооpдинат, векторы
Числа х и у называются афинными координатами точки М в системе (0, (записывается: М(х,у)). Вектор Афинная система координат (0, Теорема. Пусть
Тогда Следствие 1. Пусть даны точки А (х 1, y 1) и В (х 2, у 2). Тогда
Следствие 2. Два вектора
Афинная система координат (0, Координаты в пространстве.
Определение. Пусть в пространстве заданы три координатные оси OX, OY и OZ с некомпланарными ортами Точка 0 - начало координат, векторы Так как векторы любого вектора
Числа x, y, z называются координатами точки М (записывается: М (х, у, z)), Афинную систему часто обозначают через OXYZ. Оси OX, OY, OZ называют соответственно осями абсцисс, ординат и аппликат. Плоскости, определяемые координатными осями, т.е. OXY, OYZ, OXZ, называют координатными плоскостями. Эти плоскости делят все пространство на восемь частей, называемых координатными октантами. Если упорядоченная тройка векторов В частности, если даны точки А (х 1, у 1, z 1), В (х 2, у 2, z 2), то
Векторы
Полярные координаты.
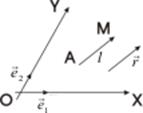
Возьмем на плоскости произвольную точку 0, которую назовем полюсом, и ось ОР, задаваемую единичным вектором
Величины r и φ называются полярными координатами точки М, r- полярный радиус, φ- полярный угол. При этом считаем, что полярные координаты точек плоскости изменяются в следующих пределах: С прямоугольными координатами полярные связаны следующими соотношениями: х = r cosφ, у = r sinφ.
Так как х 2 + у 2 = r 2, то
ПРЯМАЯ НА ПЛОСКОСТИ.
Прямая на плоскости
следует, что
- угловой коэффициент относительно выбранной системы координат. В частности, для прямоугольной системы координат (0, k = tgα, где α – угол между осью ОХ и любым направляющим вектором прямой l. Угол α называется углом наклона прямой l к оси ОХ.
Если прямая l параллельна оси ОY, то l пересекает ось OХ в некоторой точке Р(а,0). Тогда все точки прямой и только они удовлетворяют соотношению x = a - уравнение прямой, проходящей через точку параллельно оси ОУ. Заметим, что в качестве направляющего вектора такой прямой можно взять вектор Пусть прямая l проходит через точку A (а, b) и имеет угловой коэффициент k. Возьмем произвольную точку М (х, у) на прямой l. Тогда Следовательно,
Отсюда y – b = k (x - а) -уравнение прямой с угловым коэффициентом k. Пучок прямых
Пучком прямых называется совокупность всех прямых на плоскости, проходящих через некоторую точку, называемую центром пучка. Для задания уравнения пучка достаточно знать какие-либо две прямые l 1 и l 2, проходящие через центр пучка. Пусть в аффинной системе координат прямые l 1 и l 2 заданы уравнениями l 1: A1 x + B1 y + C1 = 0, l 2: A2 x + B2 y + C2 = 0.
Уравнение: A1 x + B1 y + С + λ (A2 х + В2 y + C) = 0 - уравнение пучка прямых, определяемого уравнениями l1 и l2
В дальнейшем, под системой координат будем понимать прямоугольную систему координат.
Угол между двумя прямыми
Под углом φ между двумя прямыми l 1 и l 2 будем понимать наименьший угол, на который надо повернуть одну прямую, чтобы она стала параллельной другой прямой или совпала с ней, то есть 0 £ φ £
Пусть прямые заданы общими уравнениями. Очевидно, что
cosφ=
Пусть теперь прямые l 1 и l 2 задана уравнениями с угловыми коэффициентами k 1 в k 2 соответственно. Тогда
Наконец, если
ПЛОСКОСТЬ
Общее уравнение плоскости
Пусть в прямоугольной системе координат OXYZ задана плоскость α, проходящая через точку М0(х 0, у 0, z 0). Возьмем произвольную точку М(х, у, z) Очевидно, что Раскроем скобки и обозначим D= -А x 0 - В у 0 - C z 0. Получим
A x + B y + С z + D = 0 (*)
- уравнение плоскости в общем виде или общее уравнение плоскости.
Теорема. Линейное уравнение (*) (A2+B2+C2 ≠ 0) является уравнением плоскости и обратно, любое уравнение плоскости является линейным.
Пусть 1) D = 0, тогда плоскость проходит через начало координат. 2) А = 0, тогда плоскость параллельна оси ОХ 3) А = 0, В = 0, тогда плоскость параллельна плоскости OXY.
Пусть в уравнении все коэффициенты отличны от нуля. Тогда
- уравнение плоскости в отрезках. Числа |а|, |b|, |с| указывают на величины отрезков, отсекаемых плоскостью на координатных осях.
Пучок и связка плоскостей
Пучком плоскостей называется множество всех плоскостей, проходящих через некоторую прямую, называемую осью пучка. Пусть в системе координат ОХУZ заданы две пересекающиеся плоскости α1 и α2.
Тогда уравнение пучка имеет вид А1 х + B1 y + C1 z + D1 + λ(A2 x + B2 y + C2 z + D2) = 0, где λ
Связкой плоскостей называется множество всех плоскостей, проходящих через некоторую точку, называемую центром связки. Если S0 (x 0, y 0, z 0) – центр связки, то уравнение связки с центром в точке S0 имеет вид А(х - x 0) + В(у - y 0) + С(z - z 0) = 0, где А, В и С – произвольные действительные числа, одновременно не равные нулю.
ПРЯМАЯ В ПРОСТРАНСТВЕ. КРИВЫЕ ВТОРОГО ПОРЯДКА Парабола
Определение: Параболой называется геометрическое место точек плоскости, равноудаленных от некоторой точки, называемой фокусом параболы и некоторой прямой, называемой директрисой параболы. Уравнение параболы принятo записывать в следующем виде: y2 = 2px, p>0 (1) - каноническое уравнение параболы. Свойства параболы непосредственно следуют из свойств уравнения: 1.Абсцисса любой точки параболы неотрицательна 2.Парабола проходит через начало координат. 3.Парабола симметрична относительно оси абсцисс. 4.При неограниченном возрастании абсциссы x ордината у возрастает по абсолютной величине. Точка F( Величина р называется фокальным параметром или просто параметром параболы.
Эллипс
Для составления уравнение эллипса выберем прямоугольную декартову систему координат так, чтобы ось ОХ
проходила через фокусы F1 и F2, а начало координат — точка О находилась в середине отрезка F1F2. Обозначим F1F2 = 2с. Тогда F1(-с,0), F2(c,0). Пусть М(х,у) – произвольная точка эллипса. Тогда MF1+ MF2= 2 а, а >с.
Так как
Пусть координаты точки М1(х1,у1)удовлетворяют уравнению (2). Обозначим r1 = F1M1, r2 = F2M2 — фокальные радиусы точек М1 М2. Тогда Теперь по свойствам уравнения (2) исследуем геометрические свойства эллипса. 1. Оси ОХ и ОУ являются осями симметрии эллипса. Следовательно, эллипс достаточно исследовать только в первой координатной четверти. 2. Эллипс пересекает координатные оси в точках А1(- а,0), А2(а,0), В1(0, b), В2(0,- b), называемых вершинами эллипса. 3. Эллипс расположен в прямоугольнике, ограниченном прямыми х= 4. Из уравнений следует, что при возрастании х от 0 до а в первой координатной четверти, у убывает от b до 0. По полученным свойствам строим эллипс Отрезок А1А2 и его длина 2 а называются большой осью эллипса, а отрезок B1B2 и его длина 2 b называются малой осью эллипса. Отрезок ОА1 с длиной а и отрезок ОВ1 с длиной b называются соответственно большой и малой полуосями эллипса. Длина отрезка F1F2=2 с называется фокусным расстоянием, начало координат — центр эллипса.
Уравнения х = a cost, у = b sint - параметрические уравнения эллипса.
Определение. Эксцентриситетом эллипса называется число
Так как с< а, то 0< c <1. Заметим, что у окружности оба фокуса совпадают, поэтому с = 0 и ε = 0.
Следовательно, эксцентриситет характеризует форму эллипса. Используя понятия эксцентриситета, можно выразить фокальные радиусы произвольной точки M(x,у) эллипса:
r1= а +εх, r2= а —εх Гипербола
Выберем декартову прямо-угольную систему координат ОХY так, как показано на рисунке. Тогда F1F2=2 с, F1(— с,0), F2(c,0). Для произвольной точки М(х,у), принадлежащей гиперболе, имеем МF1—MF2=
Обозначим с 2- а 2= b 2, тогда каноническое уравнение гипрболы имеет вид:
По свойствам уравнения (3) исследуем свойства гиперболы:
1. Координатные оси являются осями симметрии гиперболы. Поэтому гиперболу достаточно исследовать только в первой координатной четверти. 2. Если у = 0, то x = 3. Так как
то |х| 4. Если x возрастает от а до + 5.
- наклонные асимптоты гиперболы.
x 2— у 2= а 2
Определение. Эксцентриситетом гиперболы называется величина
Так как для гиперболы с > а, и следовательно, чем меньше ε, тем более сжата гипербола к оси ОХ.
Линии параболического типа Пусть КВП задана уравнением вида (1) и является кривой параболического типа, т.е. I2=О. Тогда I1 если I1=а11+a22=О, то I12=а112+а222+2a11a22=О, т.е.
Так как I2=a11a22—а122=О, то из (*) следует, что -(a112/2) -(а222/2)=а122.. Значит, a11=a22=a12=0 – противоречие с тем, что уравнение (1) — уравнение кривой второго порядка. Заметим, что если в уравнении (1) а12
Так как I1=а'11+а22 Будем считать, что а'11=О, а'22 рассматривается аналогично). Тогда I1=a'22 и уравнение (14) можно записать так:
Осуществим теперь параллельный перенос:
Тогда x"=x' и у"=у'+а'23/I1. Значит, в новой системе координат О"Х"У" уравнение КВП примет вид:
где
Теорема. Пусть уравнение (1) — есть уравнение параболического типа. Тогда при I3
Доказательство. Итак, для уравнения (1)
Так как I1
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 218; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.192.219 (0.25 с.) |

 множества A 2.
множества A 2.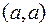
 (рефлексивность);
(рефлексивность); ,b)
,b) 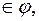 то (b,
то (b,  (симметричность);
(симметричность); то (
то ( .
. , не лежащие на двух различных параллельных прямых, и плоскость
, не лежащие на двух различных параллельных прямых, и плоскость  , проходящая через точки В и D. Тогда плоскость
, проходящая через точки В и D. Тогда плоскость 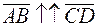 ). В противном случае, они называются противоположно направленными (обозначается
). В противном случае, они называются противоположно направленными (обозначается  ).
). , который одинаково направлен с каждым из направленных отрезков
, который одинаково направлен с каждым из направленных отрезков 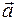 называется длина этого направленного отрезка и обозначается |
называется длина этого направленного отрезка и обозначается |  и
и  называются равными, если
называются равными, если  и
и  , при этом пишут
, при этом пишут  ). Направление нулевого вектора не определено.
). Направление нулевого вектора не определено. l, то проекция называется прямоугольной, или ортогональной.
l, то проекция называется прямоугольной, или ортогональной.

 называется проекциейвектора
называется проекциейвектора  Пусть α - некоторая плоскость и l – прямая, такая, что l не параллельна α. Через произвольную точку А пространства проведем прямую l 1 || l и обозначим точку пересечения прямой l 1 с плоскостью α через А1. Точка А1 называется проекциейточки А наплоскость α относительнопрямой l.
Пусть α - некоторая плоскость и l – прямая, такая, что l не параллельна α. Через произвольную точку А пространства проведем прямую l 1 || l и обозначим точку пересечения прямой l 1 с плоскостью α через А1. Точка А1 называется проекциейточки А наплоскость α относительнопрямой l. α
α  ), (
), ( ), (
), ( ).
).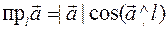 ;
;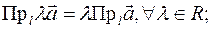
 .
.

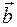 называется вектор
называется вектор  , обозначаемый
, обозначаемый  , называемый ортом, называется координатнойосью.
, называемый ортом, называется координатнойосью.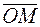 кол-
кол- . Вектор
. Вектор  и
и 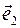 cоответственно. Тогда тройка (О,
cоответственно. Тогда тройка (О, 
 , где
, где 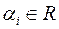


 .
.
 .
.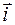 и
и 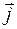 .
. соответственно. Тогда четверка (0,
соответственно. Тогда четверка (0,  имеет место разложение:
имеет место разложение: .
.


 . Таким образом, получаем систему координат, которая называется полярной системой координат.
. Таким образом, получаем систему координат, которая называется полярной системой координат.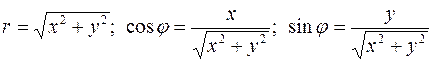
 Пусть в плоскости α задана афинная система координат (0,
Пусть в плоскости α задана афинная система координат (0,  = (m1,n1) и
= (m1,n1) и  =(m2,n2) - какие-либо направляющие векторы прямой l. Тогда из необходимого и достаточного условия коллинеарности двух векторов
=(m2,n2) - какие-либо направляющие векторы прямой l. Тогда из необходимого и достаточного условия коллинеарности двух векторов Если прямая l не параллельна оси OY, то
Если прямая l не параллельна оси OY, то  следовательно,
следовательно,
 )
)

 (0,р), где р - произвольное отличное от нуля число. В этом случае, как видим угловой коэффициент прямой не существует.
(0,р), где р - произвольное отличное от нуля число. В этом случае, как видим угловой коэффициент прямой не существует. =(х - а, у - b) - направляющий вектор прямой l.
=(х - а, у - b) - направляющий вектор прямой l.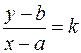

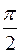
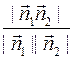

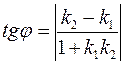
 и
и  - направляющие вектора прямых, то
- направляющие вектора прямых, то

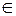 α и обозначим
α и обозначим  (А,В,C) – нормальный вектор плоскости α.
(А,В,C) – нормальный вектор плоскости α. , то есть (х - х 0) + В(у - у 0) + C(z - z 0) = 0
, то есть (х - х 0) + В(у - у 0) + C(z - z 0) = 0
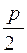 ;0) называется фокусом параболы, прямая
;0) называется фокусом параболы, прямая 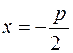 - директрисой.
- директрисой. Определение. Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых до двух данных точек F1 и F2 этой плоскости, называемых фокусами эллипса, есть величина постоянная, равная 2 а (а >0), большая, чем расстояние между фокусами.
Определение. Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых до двух данных точек F1 и F2 этой плоскости, называемых фокусами эллипса, есть величина постоянная, равная 2 а (а >0), большая, чем расстояние между фокусами. , и уравнение принимает вид:
, и уравнение принимает вид: . (2)
. (2) ,
,  , значит, r1+r2=2 a.
, значит, r1+r2=2 a. а, у =
а, у =  Если а = b, то получаем каноническое уравнение окружности
Если а = b, то получаем каноническое уравнение окружности

 .
. Определение. Гиперболой называется множество точек плоскости, абсолютная величина разности расстояний от каждой из которых до двух данных точек F1 и F2, называемых фокусами гиперболы, есть величина постоянная, равная 2 а, а >0, меньшая чем расстояние между фокусами.
Определение. Гиперболой называется множество точек плоскости, абсолютная величина разности расстояний от каждой из которых до двух данных точек F1 и F2, называемых фокусами гиперболы, есть величина постоянная, равная 2 а, а >0, меньшая чем расстояние между фокусами. (3)
(3) ,
, а. Поэтому гипербола расположена вне полосы, ограниченной прямыми x=
а. Поэтому гипербола расположена вне полосы, ограниченной прямыми x= 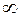 , то из (1.12) следует, что у возрастает от 0 до +
, то из (1.12) следует, что у возрастает от 0 до + 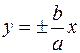
 По полученным свойствам строим гиперболу. Отрезок А1А2 и его длина 2 а называются действительной осью гиперболы, а отрезок ОА1 и его длина а — действительной полуосью. Отрезок В1В2 и его длина 2 b — мнимая ось гиперболы, а отрезок ОВ1 и его длина b — мнимая полуось. Длина отрезка F1F2=2 с называется фокусным расстоянием, начало координат — центр гиперболы.
По полученным свойствам строим гиперболу. Отрезок А1А2 и его длина 2 а называются действительной осью гиперболы, а отрезок ОА1 и его длина а — действительной полуосью. Отрезок В1В2 и его длина 2 b — мнимая ось гиперболы, а отрезок ОВ1 и его длина b — мнимая полуось. Длина отрезка F1F2=2 с называется фокусным расстоянием, начало координат — центр гиперболы. О. Действительно,
О. Действительно, (*)
(*)
 (25)
(25) , т.е.
, т.е.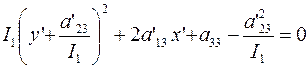 . (26)
. (26) (27)
(27)
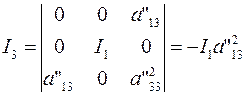 (28)
(28)


