
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение плоскости, проходящей через две заданные прямыеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
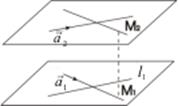
Пусть плоскость α проходят через прямые l 1 и l 2, заданные соответственно уравнениями:
Обозначим М2(x 2, y 2, z 2), Тогда
- уравнение плоскости, проходящей через две прямые. Расстояние между скрещивающимися прямыми Пусть прямые l 1 и l 2, заданные уравнениями вида (2), являются скрещивающимися. Тогда расстоянием d между ними называется длина перпендикуляра, проведенного из одно прямой на другую. Заметим, что искомое расстояние равно отрезку перпендикуляра, закаченного между плоскостями α1 и α2, где плоскости α1 и α2 одновременно параллельны векторам Тогда
Взаимное расположение прямой и плоскости
Пусть прямая l и плоскость α заданы соответственно уравнениями
A m + B n + С р = 0, А x 0 + В у 0 + C z 0 + D = 0.
2) прямая l параллельна плоскости α, если
A m + B n + Ср = О, А x 0 + В у 0 + C z 0 + D ≠ 0.
3) прямая l пересекает плоскость α если
A m + В n + С р
Угол между прямой и плоскостью
Углом между прямой l и плоскостью α называется угол φ, образованный прямой l и ее проекцией l 1 на плоскость α
Тогда
КРИВЫЕ ВТОРОГО ПОРЯДКА Парабола
Определение: Параболой называется геометрическое место точек плоскости, равноудаленных от некоторой точки, называемой фокусом параболы и некоторой прямой, называемой директрисой параболы. Уравнение параболы принятo записывать в следующем виде: y2 = 2px, p>0 (1) - каноническое уравнение параболы. Свойства параболы непосредственно следуют из свойств уравнения: 1.Абсцисса любой точки параболы неотрицательна 2.Парабола проходит через начало координат. 3.Парабола симметрична относительно оси абсцисс. 4.При неограниченном возрастании абсциссы x ордината у возрастает по абсолютной величине. Точка F( Величина р называется фокальным параметром или просто параметром параболы.
Эллипс
Для составления уравнение эллипса выберем прямоугольную декартову систему координат так, чтобы ось ОХ
проходила через фокусы F1 и F2, а начало координат — точка О находилась в середине отрезка F1F2. Обозначим F1F2 = 2с. Тогда F1(-с,0), F2(c,0). Пусть М(х,у) – произвольная точка эллипса. Тогда MF1+ MF2= 2 а, а >с.
Так как
Пусть координаты точки М1(х1,у1)удовлетворяют уравнению (2). Обозначим r1 = F1M1, r2 = F2M2 — фокальные радиусы точек М1 М2. Тогда Теперь по свойствам уравнения (2) исследуем геометрические свойства эллипса. 1. Оси ОХ и ОУ являются осями симметрии эллипса. Следовательно, эллипс достаточно исследовать только в первой координатной четверти. 2. Эллипс пересекает координатные оси в точках А1(- а,0), А2(а,0), В1(0, b), В2(0,- b), называемых вершинами эллипса. 3. Эллипс расположен в прямоугольнике, ограниченном прямыми х= 4. Из уравнений следует, что при возрастании х от 0 до а в первой координатной четверти, у убывает от b до 0. По полученным свойствам строим эллипс Отрезок А1А2 и его длина 2 а называются большой осью эллипса, а отрезок B1B2 и его длина 2 b называются малой осью эллипса. Отрезок ОА1 с длиной а и отрезок ОВ1 с длиной b называются соответственно большой и малой полуосями эллипса. Длина отрезка F1F2=2 с называется фокусным расстоянием, начало координат — центр эллипса.
Уравнения х = a cost, у = b sint - параметрические уравнения эллипса.
Определение. Эксцентриситетом эллипса называется число
Так как с< а, то 0< c <1. Заметим, что у окружности оба фокуса совпадают, поэтому с = 0 и ε = 0.
Следовательно, эксцентриситет характеризует форму эллипса. Используя понятия эксцентриситета, можно выразить фокальные радиусы произвольной точки M(x,у) эллипса:
r1= а +εх, r2= а —εх Гипербола
Выберем декартову прямо-угольную систему координат ОХY так, как показано на рисунке. Тогда F1F2=2 с, F1(— с,0), F2(c,0). Для произвольной точки М(х,у), принадлежащей гиперболе, имеем МF1—MF2=
Обозначим с 2- а 2= b 2, тогда каноническое уравнение гипрболы имеет вид:
По свойствам уравнения (3) исследуем свойства гиперболы:
1. Координатные оси являются осями симметрии гиперболы. Поэтому гиперболу достаточно исследовать только в первой координатной четверти. 2. Если у = 0, то x = 3. Так как
то |х| 4. Если x возрастает от а до + 5.
- наклонные асимптоты гиперболы.
x 2— у 2= а 2
Определение. Эксцентриситетом гиперболы называется величина
Так как для гиперболы с > а, и следовательно, чем меньше ε, тем более сжата гипербола к оси ОХ.
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 4029; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.009 с.) |

 ,
, 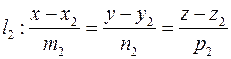 (2)
(2)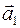 =(m 1, n 1, р 1),
=(m 1, n 1, р 1), 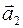 =(m 2, n 2, p 2) и М(х, у, z) произвольная точка плоскости α
=(m 2, n 2, p 2) и М(х, у, z) произвольная точка плоскости α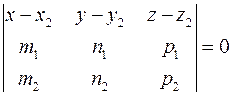

 , α: A x + B y + C z + D = 0.
, α: A x + B y + C z + D = 0.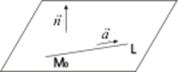 1) прямая l лежит в плоскости α, если
1) прямая l лежит в плоскости α, если
 0.
0.
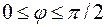 и
и .
.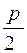 ;0) называется фокусом параболы, прямая
;0) называется фокусом параболы, прямая 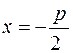 - директрисой.
- директрисой. Определение. Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых до двух данных точек F1 и F2 этой плоскости, называемых фокусами эллипса, есть величина постоянная, равная 2 а (а >0), большая, чем расстояние между фокусами.
Определение. Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых до двух данных точек F1 и F2 этой плоскости, называемых фокусами эллипса, есть величина постоянная, равная 2 а (а >0), большая, чем расстояние между фокусами. , и уравнение принимает вид:
, и уравнение принимает вид: . (2)
. (2) ,
,  , значит, r1+r2=2 a.
, значит, r1+r2=2 a. а, у =
а, у =  Если а = b, то получаем каноническое уравнение окружности
Если а = b, то получаем каноническое уравнение окружности

 .
. Определение. Гиперболой называется множество точек плоскости, абсолютная величина разности расстояний от каждой из которых до двух данных точек F1 и F2, называемых фокусами гиперболы, есть величина постоянная, равная 2 а, а >0, меньшая чем расстояние между фокусами.
Определение. Гиперболой называется множество точек плоскости, абсолютная величина разности расстояний от каждой из которых до двух данных точек F1 и F2, называемых фокусами гиперболы, есть величина постоянная, равная 2 а, а >0, меньшая чем расстояние между фокусами. (3)
(3) ,
, а. Поэтому гипербола расположена вне полосы, ограниченной прямыми x=
а. Поэтому гипербола расположена вне полосы, ограниченной прямыми x= 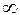 , то из (1.12) следует, что у возрастает от 0 до +
, то из (1.12) следует, что у возрастает от 0 до + 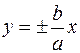
 По полученным свойствам строим гиперболу. Отрезок А1А2 и его длина 2 а называются действительной осью гиперболы, а отрезок ОА1 и его длина а — действительной полуосью. Отрезок В1В2 и его длина 2 b — мнимая ось гиперболы, а отрезок ОВ1 и его длина b — мнимая полуось. Длина отрезка F1F2=2 с называется фокусным расстоянием, начало координат — центр гиперболы.
По полученным свойствам строим гиперболу. Отрезок А1А2 и его длина 2 а называются действительной осью гиперболы, а отрезок ОА1 и его длина а — действительной полуосью. Отрезок В1В2 и его длина 2 b — мнимая ось гиперболы, а отрезок ОВ1 и его длина b — мнимая полуось. Длина отрезка F1F2=2 с называется фокусным расстоянием, начало координат — центр гиперболы.


