
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение плоскости. Уравнения прямой в пространстве.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
13.1. Даны две точки 13.2. Составить уравнение плоскости, проходящей через точку 13.3.Составить уравнение плоскости, проходящей через три точки 13.4.Определить взаимное расположение следующих пар плоскостей (перпендикулярны, параллельны, пересекаются): 1) 2) 5) 13.5. Составить уравнение плоскости, которая проходит через т. перпендикулярно двум плоскостям 2х-z+1=0 и у=0. 13.6. Установить, что три плоскости х-2у+z-7=0, 2х+у-z+2=0, х-3у+2z-11=0, имеют одну общую точку и найти ее. 13.7. Доказать, что три плоскости 7х+4у+7z+1=0, 2х-у-z+2=0, х+2у+3z-1=0, проходят через одну прямую. 13.8.Доказать, что три плоскости 2х-у+3z-5=0, 3х+у+2z-1=0, 4х+3у+z+2=0, пересекаются по трем различным параллельным прямым. 13.9.Найти расстояние между параллельными плоскостями: 1) 2) 13.10. Составить уравнения плоскостей, которые делят пополам двугранные углы, образованные пересекающимися плоскостями: 1) 2) 13.11. Составить уравнение плоскости, проходящей через прямую пересечения плоскостей 2х-у+3z-5=0 и х+2у-z+2=0 параллельно вектору 13.12. Составить уравнение плоскости, проходящей через прямую перпендикулярно плоскости х+19у-7z-11=0. 13.13. Дана прямая, составить канонические и параметрические уравнения прямой: 1) 13.14. Определить взаимное расположение прямых (перпендикулярны, параллельны): 1) 2) x=2t, y=3t-2, z=-6t+1 и 3) 13.15. Определить косинус угла между прямыми:
13.16. Доказать, что прямые, заданные параметрически
13.17. Доказать, что прямая x=3t-2, y=-4t+1, z=4t-5 параллельна плоскости 4x-3y-6z-5=0. 13.18. Доказать, что прямая 13.19. Найти точку пересечения прямой 13.20. Найти проекцию точки Р(2,-1,3) на прямую x=3t, y=5t-7, z=2t+2. 13.21. Найти проекцию точки Р(5,2,-1) на плоскость 2x-y+3z+23=0. 13.22. Найти расстояние от точки Р(1,-1,-2) до прямой 13.23. Вычислить кратчайшее расстояние между прямыми: 1) 2) x=2t-4, y=-t+4, z=-2t-1 и x=4t-5, y=-3t+5, z=-5t+5. КРИВЫЕ ВТОРОГО ПОРЯДКА
Найти каноническую систему координат и канонический вид кривой и построить ее в канонической системе координат. 14.1. а) б) в) г) д) 14.2. а) б) в) г) д) 14.3. а) б) в) г) д) е)
14.4. а) б) в) г) д) е) ж) з) и)
к) л)
ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ №3 Найти каноническое уравнение кривой и построить ее 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30.
Ответы на задания по матричной алгебре. Глава 1. КОМПЛЕКСНЫЕ ЧИСЛА. КОМБИНАТОРИКА. БИНОМ НЬЮТОНА. КОМПЛЕКСНЫЕ ЧИСЛА 1.1. 1) 5i+12; 2) 10) 1.2. 1) 1.3. 1) 1 4) 2 7) 10) 13) 16) 19) 1.4. 1) -1, 6) 8) 1.5. 1) i; 2) 32i; 3) 64; 4) –i; 5) 4- 4i; 6) 8i; 7) 8i; 8) 1.7. I; 3) -1; 4) i. 1.9. а) симметрично относительно оси ох; б) симметрично относительно начала координат; в) на окружности радиуса 1.10. 1) 1.11. 1) 0, 1.12. точка Z лежит на прямых 1.13. КОМБИНАТОРИКА
1.15. 1) 1; 2) 120; 3) 5040; 4) 56; 5) 1/7980. 1.16. 1) 1.18. 1) 28; 2) 2380; 3) 6; 4) 17; 5) 101. 1.22. БИНОМ НЬЮТОНА 1.23. 1) 3) 1.24. 1) 6188 1.26. 1) 4) Глава 2. МНОГОЧЛЕНЫ 2.1. 1) 5) 2.2. 1) 2.3. 1) 2.5. 1) z = - 2; 2) z = 2; 3) нет целых корней; 4) 6) нет целых корней. 2.7. 1) 2.10. a = -6, b= -2. 2.11. 1) k=2; 2) k=3; 3) k=4; 4) k=3. 2.12. 1) 2.14. 1) 2.15. 1) 2.16. 1) 3) 2.17. 1) 3) Глава 3. МАТРИЦЫ. ОПРЕДЕЛИТЕЛИ. 3.1. 1) 3.3. 3.5. 1) 3.6. 3.7. 1) 3.8. 1) 4) 3.9. 1) Вид определяется неоднозначно, например: 2) 3.10. 1) ОПРЕДЕЛИТЕЛИ 3.12. 1) 1; 2) -2; 3) -1; 4) 0; 5) -3; 6) 13. 3.14. 1) 40; 2) -3; 3) abc; 4) abc; 5) 3.16. 3) Умножим элементы 1-го столбца на 10 и прибавим по 2-му столбцу.
3.17. 1) 1; 2) 5; 3) 0; 4) 15; 5) -2i; 6) abcd; 7) Глава 4. ОБРАТНАЯ МАТРИЦА. РАНГ МАТРИЦЫ. ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ВЕКТОРОВ. 4.2. 1) 4.3. 1) r = 0; 2) r = 1; 3) r = 2; 4) r = 2; 5) r = 2; 6) r = 2; 7) r = 2; 8) r = 4. 4.4. матрицы с нулевыми элементами. 4.5. матрицы со всеми пропорциональными строками или столбцами, а также матрицы, имеющие одну ненулевую строку или столбец.
4.6. r = n (числу ненулевых элементов). 4.7. 1) возможно, не всегда; 2) возможно, выполняется не всегда; 3) возможно, выполняется не всегда; 4) возможно, выполняется не всегда; 5) возможно, выполняется не всегда; 6) возможно, выполняется всегда. 4.8. 1) (1,4,-7,7); 2) (0,0,0,0). 4.9. 1) система линейно независима; 2) система линейно независима; 3) система линейно независима; 4) система линейно зависима; 5) система линейно зависима; 6) система линейно независима. Глава 5. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ. 5.1. 1) система совместна, х =1, у =1, z =1; 2) система совместна, x = -1, y = 0, z = 1; 3) система несовместна; 4) система несовместна; 5) система совместна, 5.2. 1) общее решение: ФСР: 2) общее решение: 3) общее решение: 4) общее решение: 5) общее решение:
6) общее решение:
5.3. 1) система совместная, неопределенная. Общее решение: х = (1, -С, С); 2) система совместная, неопределенная. Общее решение: 5.4. 1) определена, 3) неопределенна а= -3, 5.5. 1) определена, при 3) неопределенна, при а= 1. Глава 6. СОБСТВЕННЫЕ ВЕКТОРЫ И СОБСТВЕННЫЕ ЗНАЧЕНИЯ МАТРИЦЫ. ЛИНЕЙНЫЕ ПРОСТРАНСТВА. 6.1. 1) 2) 3) 5) 6) 7) 8) 9) 10) 11) 12) 6.2.
собственные значения равны диагональным элементам. 6.4. по аналогии с 6.2. 6.5. 6.6. 1) является; 2) не является; 3) не является; 4) является; 5) является; 6) является; 7) не является; 8) является; 9) является; 10) не является; 11) не является; 12) является; 13) является; 14) является; 15) является; 16) является; 17) не является; 18) является; 19) не является; 20) является. Глава 7.
|
||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 563; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.172.137 (0.012 с.) |

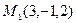 и
и  . Составить уравнение плоскости перпендикулярной прямой
. Составить уравнение плоскости перпендикулярной прямой 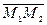 , проходящей через
, проходящей через  .
. параллельно двум векторам
параллельно двум векторам  и
и  .
. ,
,  и
и  .
. ;
; ; 3)
; 3)  ; 4)
; 4)  ;
;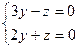 ; 6)
; 6)  .
.
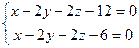 ;
; ; 3)
; 3) 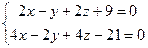 .
. ;
; .
.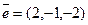

 ; 2)
; 2)  ; 3)
; 3)  .
. ,
,  ;
;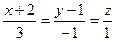 и
и  .
. и
и  .
.
 и
и  , пересекаются.
, пересекаются.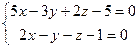 лежит в плоскости 4x-3y+7z-7=0.
лежит в плоскости 4x-3y+7z-7=0. и плоскости 2x+3y+z-1=0.
и плоскости 2x+3y+z-1=0. .
. и
и  ;
;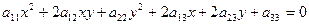

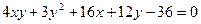
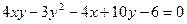



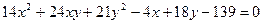






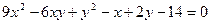











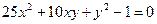



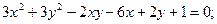



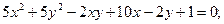
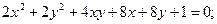
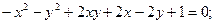




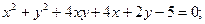
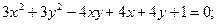

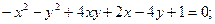

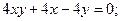
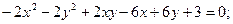








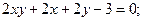

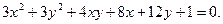
 ; 3) 5-12i; 4) 2i-2; 5) i; 6) i+1; 7) 8-2i; 8) 23-14i; 9)
; 3) 5-12i; 4) 2i-2; 5) i; 6) i+1; 7) 8-2i; 8) 23-14i; 9) 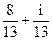 ;
; ; 11) 0,8+0,6i; 12) 0,25-0,25i.
; 11) 0,8+0,6i; 12) 0,25-0,25i. 2)
2)  3)
3)  4)
4)  5)
5)  2; 6)
2; 6) 

 ; 2) 5
; 2) 5  ;
; ; 5)
; 5) 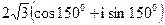 ; 6)
; 6)  ;
; ; 8) 1
; 8) 1  ;
; ; 11)
; 11)  ; 12)
; 12) 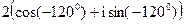 ;
; ; 14)
; 14)  ; 15)
; 15) 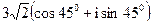 ; 17)
; 17) 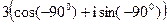 ; 18)
; 18)  ;
; ; 20)
; 20)  ; 21)
; 21)  .
. ; 2)
; 2) 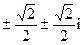 ; 3)
; 3)  ,
,  ; 4) 1,
; 4) 1,  ; 5)
; 5)  ,
, 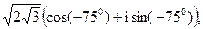
 ; 7) -i,
; 7) -i,  ;
; ,
,  ; 9)
; 9) 
 ,
,  .
.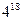 ; 9) 1.
; 9) 1. ,
,  ,
,  ,
,  , где
, где  .
. с центром в начале координат, на лучах, составляющих углы
с центром в начале координат, на лучах, составляющих углы  ,
,  с положительным направлением оси ох.
с положительным направлением оси ох. ,
,  ; 2)
; 2)  ,
,  ,
, 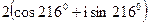 ,
, 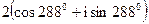 ; 4) i+1,
; 4) i+1,  ,
,  ; 5)
; 5)  ,
,  ,
,  .
. ; 2)
; 2)  ,
,  ,
,  ; 3) ki,
; 3) ki,  .
. .
. . 1.14. решений нет.
. 1.14. решений нет. , 2)
, 2)  . 1.17. 7.
. 1.17. 7. .
. ; 2)
; 2)  ;
; ; 4)
; 4)  ; 5) - 44i+117; 6) -32i.
; 5) - 44i+117; 6) -32i. ; 2) 19448
; 2) 19448  ; 3) 136
; 3) 136  ; 4) 17
; 4) 17  .
. ; 2)
; 2)  ; 3)
; 3)  ;
; .
. ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ;
; ; 6)
; 6)  .
. ; 2)
; 2) 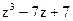 ; 3)
; 3)  ,
,  ; 4)
; 4) 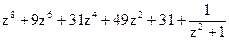 .
. ; 2)
; 2)  ; 3)
; 3)  ,
, 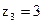 ; 4)
; 4)  ,
,  ,
,  ; 5)
; 5) 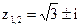 ,
, 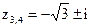 ,
,  ,
,  ; 6)
; 6)  ,
,  .
. ,
,  ; 5) z =2;
; 5) z =2;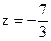 ; 2)
; 2)  ,
,  .
.
 ; 2)
; 2) 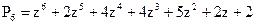 .
. ; 2)
; 2) 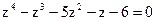 .
. ; 2)
; 2) 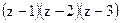 ;
; ; 4)
; 4)  .
.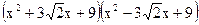 ; 2)
; 2)  ;
; ; 4)
; 4)  .
. ; 2)
; 2)  . 3.2. 1) -1; 2)
. 3.2. 1) -1; 2)  ; 3)
; 3)  ; 4)
; 4) 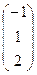 .
. . 3.4. 1) не существует; 2)
. 3.4. 1) не существует; 2)  ; 3)
; 3) 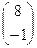 ; 4) не существует.
; 4) не существует. ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
. , т.к., если
, т.к., если  ,
,  ,
,  ,
,  .
. ; 2)
; 2)  .
. ; 2)
; 2)  ; 3)
; 3) 

 ;
; ; 5)
; 5)  ; 6)
; 6)  .
. ;
; .
.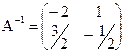 ; 2)
; 2)  .
. ; 6) 1; 7) -i; 8) 9i+15.
; 6) 1; 7) -i; 8) 9i+15. на определитель,
на определитель,  исходный определитель делится на 19.
исходный определитель делится на 19. ; 8)
; 8)  .
. ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.

 .
.


 6) система совместна,
6) система совместна, 



 ,
, 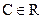 ; частное решение:
; частное решение:  ;
; ,
,  ;
;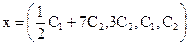 ; частное решение:
; частное решение:  ; ФСР:
; ФСР:  ,
, 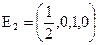 ,
, 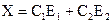 ;
; ; частное решение:
; частное решение:  ; ФСР: n – r = 3-1=2,
; ФСР: n – r = 3-1=2,  ,
,  :
:  ;
;  ,
,  :
:  ,
,  ; частное решение:
; частное решение:  ; ФСР: n – r = 3,
; ФСР: n – r = 3,  :
:  ;
;  ,
,  ,
, 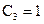 :
:  ;
;  ;
;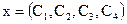 ; частное решение:
; частное решение:  ; ФСР: n – r = 4,
; ФСР: n – r = 4,  :
:  ;
;  ,
,  ;
; 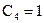 :
:  ;
; ;
; ; частное решение:
; частное решение: 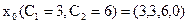 ; ФСР: n – r = 3-1=2,
; ФСР: n – r = 3-1=2,  ;
; ,
,  .
. , r (А) = 3; 2) несовместна, а= -3,
, r (А) = 3; 2) несовместна, а= -3,  ;
; .
. ,
,  r (А) = 3; 2) несовместна, при а= -2;
r (А) = 3; 2) несовместна, при а= -2;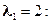
 ,
, 
 ,
,  ;
;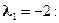
 ,
, 
 ,
, 
 ; 4)
; 4) 

 ,
, 
 ,
, 
 ;
; ,
, 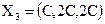 ;
;
 ,
,  комплексные;
комплексные;
 ;
; 
 ;
; ,
, 

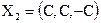 ,
, 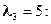
 ;
;
 ,
,  ,
,  .
.



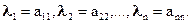


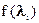 .
.


