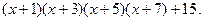Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы аналитической геометрииСодержание книги
Поиск на нашем сайте
1.1. Векторы. Линейные операции над векторами. 1.2. Декартова прямоугольная система координат.Деление отрезка в данном отношении. 1.3. Скалярное произведение векторов. Свойства скалярного произведения. Направляющие косинусы. 1.4. Векторное произведение векторов. Свойства векторного произведения. Геометрический смысл векторного произведения. 1.5. Смешанное произведение векторов. Геометрический смысл смешанного произведения. 1.6. Необходимые и достаточные условия ортогональности, коллинеарности и компланарности векторов. 1.7. Уравнения прямой на плоскости. Расстояние от точки до прямой. 1.8. Уравнения плоскости. Уравнения прямой в пространстве. 2. КРИВЫЕ ВТОРОГО ПОРЯДКА. 2.1. Инварианты. 2.2. Классификация по инвариантам и собственным числам. 3. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА.
ТЕМЫ ПРАКТИЧЕСКИХ ЗАНЯТИЙ. 1. Комплексные числа. 2. Комбинаторика. Бином Ньютона 3. Многочлены. Индивидуальное задание. 4. Матрицы, определители 5. Обратная матрица. Ранг матрицы. Линейная зависимость векторов. 6. Системы линейных уравнений. 7. Собственные числа и собственные векторы. Линейные пространства. Контрольная работа. 8. Базис. Матрица перехода. Процесс ортогонализации. 9. Матрицы операторов. Квадратичные формы. Приведение к диагональному виду. Критерий Сильвестра. 10. Число и вектор Фробениуса. Продуктивность матриц. 11. Векторы. Скалярное произведение. 12. Векторное и смешанное произведение векторов. 13. Уравнения прямой на плоскости. 14. Уравнение плоскости. Уравнения прямой в пространстве. 15. Кривые второго порядка. Контрольная работа.
ФОРМЫ КОНТРОЛЯ В семестре проводятся две контрольные работы и индивидуальное задание, которые оцениваются в баллах. В конце семестра проводится экзамен. Баллы, полученные на экзамене и в семестре суммируются, и по их результатам выставляется оценка. ВОПРОСЫ К ЭКЗАМЕНУ
СПИСОК ЛИТЕРАТУРЫ:
КОМПЛЕКСНЫЕ ЧИСЛА. КОМБИНАТОРИКА. БИНОМ НЬЮТОНА. КОМПЛЕКСНЫЕ ЧИСЛА 1.1. Выполнить действия:
1.2. Решить уравнения и проверить подстановкой корней в уравнение: 1. 2. 3. 4. 5. 6. 1.3. Представить в тригонометрической форме комплексные числа:
1.4. Найти все значения корней:
1.5. Вычислить:
1.6. 1) Доказать, что сумма и произведение взаимно сопряженных комплексных чисел являются действительными числами. 2) Доказать равенства: 1. 2. 3. 4. 1.7. Найти формулы для вычисления степеней числа i. 1.8. Найдите: 1) 1.9. Как расположены на комплексной плоскости1) сопряженные числа; 2) противоположные числа; 3) корни n -ой степени? 1.10. Решить уравнения:
1.11.Решить уравнения: 1. 2. 3.
1.12. Где находится точка z комплексной плоскости, если точка 1.13. Найти действительные корни уравнения КОМБИНАТОРИКА 1.14. Найдите: 1) 0!; 2) 5!; 3) 7!; 4) 1.15. Сократите дробь: 1) 1.16. Решить уравнение: 1.17. Найдите: 1) 1.18. Докажите, что 1.19. Докажите равенство: 1. 1.20. Докажите, что 1.21. В некотором царстве все люди отличаются набором зубов. Каково население этого царства?
БИНОМ НЬЮТОНА 1.22. Разложите по биному: 1. 1.24. Найдите: 1) пятое; 2) 10; 3) 15; 4) 16 слагаемое в разложении 1.25. Докажите, что 1) 2) Сумма биномиальных коэффициентов, стоящих на четных местах, равна сумме биномиальных коэффициентов, стоящих на нечетных местах. 1.26. Пользуясь формулой Муавра и биномом Ньютона выразить через степени 1)
МНОГОЧЛЕНЫ 2.1. Разделить: 1. 2. 3. 4. 5. 6. 2.2. Выделить целую и дробную часть рациональной функции: 1. 3. 2.3. Решить уравнения: 1. 2. 3. 4. 5. 6. 2.4. Доказать, что целые корни алгебраического уравнения с целыми коэффициентами являются делителями свободного члена. 2.5. Найти целые корни уравнений: 1. 3. 5. 2.6. Доказать, что каждый рациональный корень алгебраического уравнения с целыми коэффициентами представим в виде
2.7. Найти рациональные корни уравнений: 1. 2. 2.8. Доказать, что если уравнение 2.9. Доказать, что каждый многочлен нечетной степени с действительными коэффициентами имеет, по крайней мере, один действительный корень. 2.10. При каких значениях а и b число 2.11. Определить кратность корня 1. 2. 3. 4. 2.12. Найти приведенный многочлен наименьшей степени с действительными коэффициентами, корнями которого являются: 1. 2. 2.13. Доказать, что если
……………………………………
2.14. Уравнение 1. имеет корни 2. имеет корни Найти третий корень уравнения. 2.15. Записать уравнение, корнями которого являются: 1. 2. 2.16.Представить многочлен в виде произведения линейных множителей: 1. 3. 2.17.Представить многочлен в виде произведения неприводимых множителей с действительными коэффициентами: 1. 3.
ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ №1
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 224; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.187.121 (0.008 с.) |

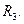
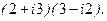
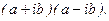
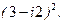
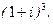
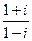 .
.
 .
.
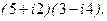
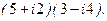

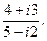

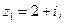

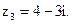






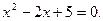
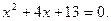
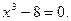


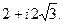
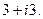
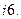

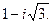
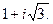

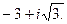
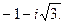
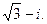
 .
.
 .
.
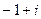 .
.
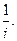
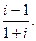
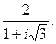
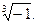


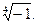
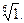
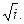
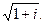
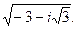

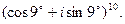
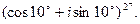

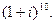
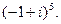
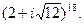
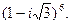
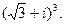

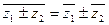 .
.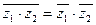 .
.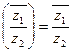 .
.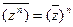 .
. ; 2)
; 2) 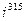 ; 3)
; 3)  ; 4)
; 4)  .
.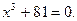

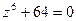 .
.
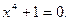
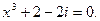
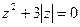 ;
;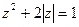 ;
;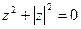 .
. принадлежит мнимой оси?
принадлежит мнимой оси?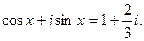
 ;5)
;5)  .
.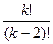 ; 2)
; 2)  .
.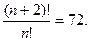
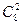 ; 2)
; 2) 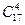 ; 3)
; 3) 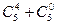 ; 4)
; 4)  ; 5)
; 5) 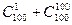 .
.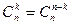 .
. ; 2.
; 2. 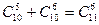 .
.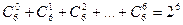 .
.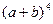 ; 2.
; 2.  ; 3.
; 3. 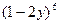 ; 4.
; 4. 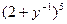 ; 5.
; 5. 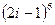 ; 6.
; 6.  .
.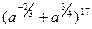 .
.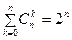 ;
; и
и 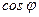 следующие функции кратных углов:
следующие функции кратных углов: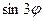 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.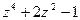 на
на  ;
;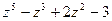 на
на  ;
;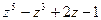 на
на 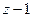 ;
; на
на  ;
;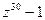 на
на 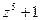 ;
;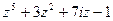 на
на  .
. ; 2.
; 2.  ;
;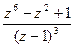 ; 4.
; 4.  .
.
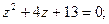
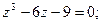
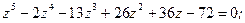
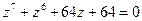 ;
;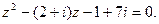
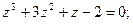 2.
2. 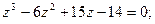
 4.
4. 
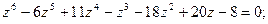 6.
6. 
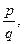 где р - делитель свободного члена, q - делитель старшего коэффициента уравнения
где р - делитель свободного члена, q - делитель старшего коэффициента уравнения 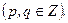
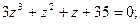
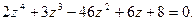
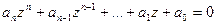 с действительными коэффициентами имеет корень
с действительными коэффициентами имеет корень 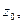 то
то 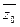 является тоже корнем этого уравнения.
является тоже корнем этого уравнения.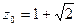 является корнем уравнения
является корнем уравнения 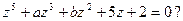
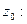
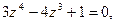
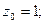

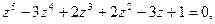
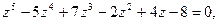
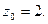
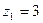 и
и 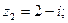
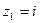 (корень кратности 2) и
(корень кратности 2) и 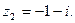
 корни уравнения
корни уравнения 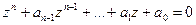 , то они связаны с коэффициентами уравнения формулами Виета:
, то они связаны с коэффициентами уравнения формулами Виета: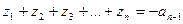
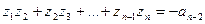
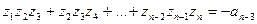
 .
.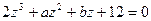

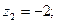

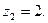

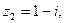
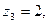
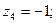
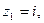
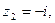
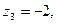
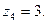
 2.
2. 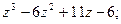
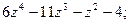 4.
4. 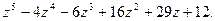
 2.
2. 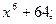
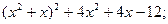 4.
4.