
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выполнить действия в алгебраической форме. Результат записать в тригонометрической и показательной формах.Содержание книги
Поиск на нашем сайте
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. Вычислить по формулам Муавра. 1. 3. 5. 7. 9. 11. 13. 15. 17. 19. 21. 23. 25. 27. 29. Выразить sin4 Найти разложение по биному Ньютона 1. 3. 5. 7. 9. 11. 13. 15. 17. 19. 21. 23. 25. 27. 29. 4. Разделить многочлен f(x) на многочлен х- 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. 5. Выделить целую и дробную часть рациональной функции: 1.
3.
5.
7.
9.
11.
13.
15.
17.
19.
21.
23.
25.
27.
29. Разложить на линейные множители в С и неприводимые (линейные и квадратичные) множители в R. Сделать проверку. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. МАТРИЦЫ. ОПРЕДЕЛИТЕЛИ. МАТРИЦЫ 3.1. Вычислить: 1) 3.2. Вычислить: 1) 3) 3.3. Матрица А имеет размер
3.4. Проверить существует ли произведение матриц, если да, то вычислить его. 1) 3) 3.5. Протранспонировать матрицу: 1) 3.6. Всегда ли верно матричное тождество 3.7. Вычислить 1) 2) 3.8. Вычислить 1) 3) 5) 3.9. Найти все матрицы, перестановочные с матрицей 1) 3.10. Найти обратные матрицы для 1) 3.11. «Следом» квадратной матрицы называется сумма элементов главной диагонали. Доказать, что след
ОПРЕДЕЛИТЕЛИ. 3.12. Вычислить определители 1) 3) 5) 3.13. Доказать, что для равенства нулю определителя второго порядка, необходимо и достаточно, чтобы его строки были пропорциональны. (коэффициент пропорциональности может быть равен 0). 3.14. Вычислить: 1) 4) 7) 3.15. Доказать, что определитель диагональной матрицы равен произведению диагональных элементов.
3.16. Используя свойства определителя, доказать тождества: 1) 2) 3) Числа 19, 38 делятся на 19. Не вычисляя определителя, докажите, что определитель 3.17. Вычислить: 1)
4) 7) Вычислить 1) и 2) методом Гаусса.
ОБРАТНАЯ МАТРИЦА. РАНГ МАТРИЦЫ. ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ВЕКТОРОВ. ОБРАТНАЯ МАТРИЦА 4.1. Доказать, что 4.2. Найти обратные матрицы и сделать проверку ( 1. РАНГ МАТРИЦЫ 4.3. Найти ранг матриц: 1. 5. 4.4. Дать описание всех матриц ранга 0. 4.5. Дать описание всех матриц ранга 1. 4.6. Доказать, что ранг диагональной матрицы равен числу ее элементов, отличных от нуля. 4.7. Указать, какие из следующих соотношений возможны. Какие верны для произвольной пары матриц? 1. r(A+B)=r(A); 2. r(A+B)=max(r(A),r(B)); 3. r(A+B)=min(r(A),r(B)); 4. r(A+B)=r(A)+r(B); 5. r(A+B)<r(A)+r(B); 6. r(A+B) ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ВЕКТОРОВ 4.8. Найти линейную комбинацию 1. 2. 4.9. Выяснить, являются ли следующие системы векторов линейно зависимыми: 1. 4. 4.10. Доказать, что система векторов, содержащая два равных вектора, линейно зависима. 4.11. Доказать, что система векторов, содержащая нулевой вектор, линейно зависима. 4.12. Доказать, что если часть системы векторов, линейно зависима, то и вся система линейно зависима.
ЗАДАЧИ ПОВЫШЕННОЙ СЛОЖНОСТИ 1. Доказать теорему Виета для кубического уравнения:
2. Доказать, что если уравнение 3. Доказать теорему Виета для уравнения четвертой степени: 4. Доказать, что целые корни алгебраического уравнения с целыми коэффициентами являются делителями свободного члена. 5.Доказать, что каждый многочлен нечетной степени с действительными коэффициентами имеет по крайней мере один действительный корень. 6. Используя формулу Муавра, бином Ньютона, и равенство комплексных чисел, выразить sin 4 x через cos x и sin x. 7. Найти сумму биноминальных коэффициентов, т.е. 8. Вычислить:
9.Дана невырожденная матрица А. Найти определитель обратной матрицы, если известно, что 10. Доказать единственность обратной матрицы для невырожденной матрицы. 11. Доказать, что вырожденная матрица не имеет обратной.
12. Доказать, что система векторов, содержащая нулевой вектор, линейно зависима. 13. Доказать, что система векторов, содержащая два равных вектора, линейно зависима. 14. Доказать, что система векторов, содержащая два пропорциональных вектора, линейно зависима. 15. Доказать, что 16. Доказать, что 17. Доказать, что если векторы 18. Доказать, что если 19. Вычислить 20. Доказать, для матриц второго порядка, что 21. «Следом» Доказать, что 22. «Следом» Доказать, что 23. Доказать, что если многочлен с действительными коэффициентами имеет корень 24. Используя формулу Муавра, бином Ньютона и равенство комплексных чисел выразить cos 4x через cos x и sin x. 25. Доказать, что 26. Доказать, что определитель диагональной матрицы равен произведению ее диагональных элементов. 27. Справедливо ли тождество 28. Числа 105, 147, 189 делятся на 21. Объясните без вычислений, почему определитель 29. Справедливо ли матричное тождество: (для матриц 2-го порядка). 30. Справедливо ли матричное тождество: (для матриц 2-го порядка). 31. Справедливо ли матричное тождество: (для матриц 2-го порядка). 32. Доказать, что для любых трех линейно независимых векторов, 33. Как изменится определитель, если все элементы в нем заменить на сопряженные? 34.Вычислить f(4), пользуясь схемой Горнера и теоремой Безу 35. Доказать, что если два многочлена f(x) и g(x), степени которых не меньше n, имеют равные значения при (n+1) значении аргументов, то эти многочлены равны.
СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ. 5.1. Доказать совместность и найти решение систем линейных уравнений: а) методом Гаусса; б) по формулам Крамера; в) методом обратной матрицы. 1) 3) 5) 5.2. Найти общее решение, фундаментальную систему уравнений и одно частное решение однородных систем линейных уравнений. 1) 3) 5) 5.3. Исследовать на совместность и найти решения систем: 1) 5.4. Определить при каких а и в система 1) определена; 2) несовместна; 3) не определена. 5.5. Определить при каких а система 2) несовместна; 3) не определена.
ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ №2 1.Найти определитель: а) разложением по строке (столбцу); б) методом Гаусса. 1. 3. 5. 7. 9. 11. 13. 15. 17. 19. 21. 23. 25. 27.
29. 2. Доказать совместность и решить: 1) методом Гаусса; 2) методом Крамера; Матричным методом. Сделать проверку. 1. 3. 5. 7. 9. 11. 13. 15. 17. 19. 21. 23. 25. 27. 29.
|
||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 654; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.205.161 (0.01 с.) |

 16.
16. 
 17.
17. 

 18.
18. 
 19.
19. 
 20.
20. 
 21.
21.  22.
22. 
 23.
23. 
 24.
24. 
 25.
25. 
 26.
26. 
 27.
27. 
 28.
28. 
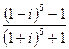
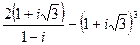 30.
30. 
 ,
,  2.
2. 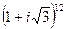 ,
, 
 ,
,  4.
4.  ,
, 
 ,
,  6.
6.  ,
, 
 ,
,  8.
8.  ,
, 
 ,
,  10.
10.  ,
, 
 ,
,  12.
12.  ,
, 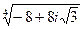
 ,
,  ,
, 
 ,
,  16.
16.  ,
, 
 ,
,  18.
18.  ,
, 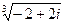
 ,
,  20.
20.  ,
, 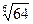
 ,
,  22.
22. 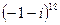 ,
, 
 ,
,  24.
24. 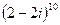 ,
,  ,
,  26.
26.  ,
, 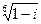
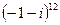 ,
, 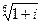 28.
28.  ,
, 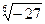
 ,
, 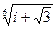 30.
30.  ,
, 
 и cos4
и cos4  ,
,  2.
2.  ,
, 
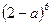 ,
,  4.
4.  ,
, 
 ,
,  6.
6.  ,
, 
 ,
,  8.
8.  ,
, 
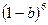 ,
,  10.
10.  ,
, 
 ,
,  12.
12. 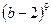 ,
, 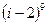
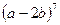 ,
,  ,
, 
 ,
,  16.
16.  ,
, 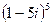
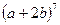 ,
, 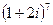 18.
18.  ,
, 
 20.
20.  ,
, 
 ,
,  22.
22. 
 ,
,  24.
24. 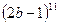 ,
, 
 ,
,  26.
26.  ,
, 
 ,
, 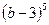 ,
,  ,
,  30.
30.  ,
,  по схеме Горнера
по схеме Горнера


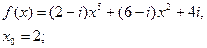


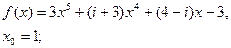






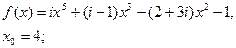



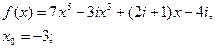





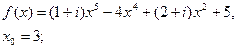





 2.
2. 
 4.
4. 
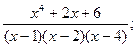 6.
6. 
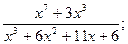 8.
8. 
 10.
10. 
 12.
12. 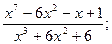
 14.
14. 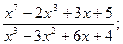
 16.
16. 
 18.
18. 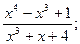
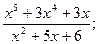 20.
20. 
 22.
22. 
 24.
24. 
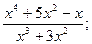 26.
26. 
 28.
28. 
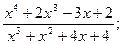 30.
30. 






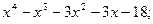
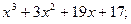



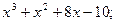




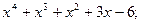




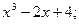






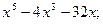


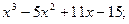









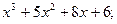
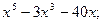
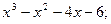
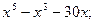







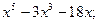






 2)
2) 
 2)
2) 
 4)
4) 
 , матрица С – размера
, матрица С – размера 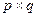 . Существует ли произведение
. Существует ли произведение  ? Каковы размеры матриц B и ABC?
? Каковы размеры матриц B и ABC? 2)
2) 
 4)
4) 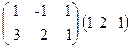
 2)
2)  3)
3)  4)
4) 
 . Привести примеры перестановочных матриц.
. Привести примеры перестановочных матриц. , если
, если ,
, 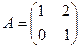
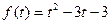 ,
, 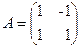
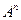 .
. , 2)
, 2)  ,
, , 4)
, 4)  ,
,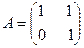 , 6)
, 6) 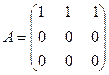 .
. , 2)
, 2)  .
. , 2)
, 2)  .
. равен следу
равен следу  .
. , 2)
, 2)  ,
,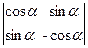 , 4)
, 4)  ,
, , 6)
, 6)  .
.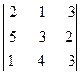 2)
2)  3)
3) 
 5)
5) 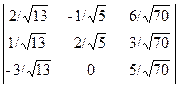 6)
6) 
 8)
8)  .
.
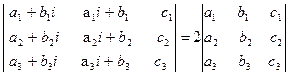
 делится на 19.
делится на 19. 2)
2)  3)
3) 
 5)
5)  6)
6) 
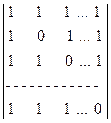 8)
8)  .
.
 ):
): 2.
2. 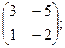 3.
3. 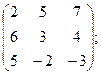 4.
4. 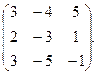
 2.
2. 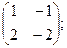 3.
3.  4.
4. 
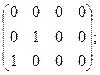 6.
6.  7.
7. 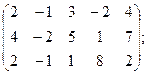 8.
8. 
 r(A)+r(B).
r(A)+r(B). векторов:
векторов:
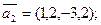




 2.
2.  3.
3. 
 5.
5.  6.
6. 

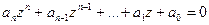 с действительными коэффициентами имеет комплексный корень
с действительными коэффициентами имеет комплексный корень  то и
то и  тоже является корнем этого уравнения.
тоже является корнем этого уравнения.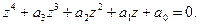





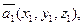

 линейно зависимы, то определитель
линейно зависимы, то определитель 
 корень многочлена,
корень многочлена, 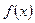 , то остаток от деления многочлена на
, то остаток от деления многочлена на  равен 0.
равен 0.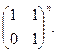


 квадратной матрицы называется сумма элементов главной диагонали.
квадратной матрицы называется сумма элементов главной диагонали.

 .
. квадратной матрицы называется сумма элементов главной диагонали.
квадратной матрицы называется сумма элементов главной диагонали. .
. то он делится (без остатка) на многочлен
то он делится (без остатка) на многочлен 
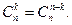
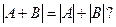
 делится на 21.
делится на 21.
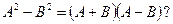

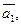

 векторы
векторы 
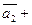
 линейно независимы.
линейно независимы.
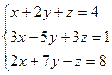 2)
2) 
 4)
4) 
 6)
6) 
 2)
2) 
 4)
4) 
 6)
6) 
 2)
2) 
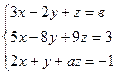 :
: : 1) определена;
: 1) определена; 2.
2. 
 4.
4. 
 6.
6. 
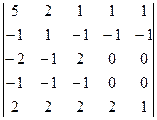 8.
8. 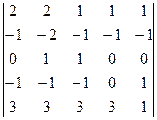
 10.
10. 
 12.
12. 
 14.
14. 
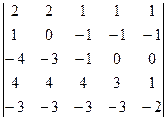 16.
16. 
 18.
18. 
 20.
20. 
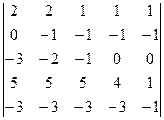 22.
22. 
 24.
24. 
 26.
26. 
 28.
28. 
 30.
30. 
 2.
2. 
 4.
4. 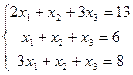
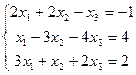 6.
6. 
 8.
8. 
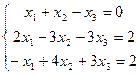 10.
10. 
 12.
12. 
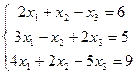 14.
14. 
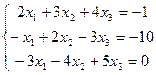 16.
16. 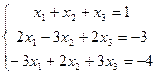
 18.
18. 
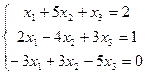 20.
20. 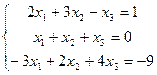
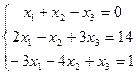 22.
22. 
 24.
24. 
 26.
26. 
 28.
28. 
 30.
30. 



