
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Найти общее решение, фундаментальную систему решений и частное решение. Сделать проверку частного решения.Содержание книги
Поиск на нашем сайте
1. 3. 5. 7. 9. 11. 13. 15. 17. 19. 21. 23. 25. 27. 29. СОБСТВЕННЫЕ ВЕКТОРЫ И СОБСТВЕННЫЕ ЗНАЧЕНИЯ МАТРИЦЫ. ЛИНЕЙНЫЕ ПРОСТРАНСТВА. СОБСТВЕННЫЕ ВЕКТОРЫ И СОБСТВЕННЫЕ ЗНАЧЕНИЯ МАТРИЦЫ 6.1. Найти собственные значения и собственные векторы матриц: 1. 5. 9. 6.2. Найти собственные значения треугольной матрицы:
6.3. Доказать, что характеристический многочлен 6.4. Доказать, что собственные значения диагональной матрицы совпадают с ее диагональными элементами. 6.5. Доказать, что если х- собственный вектор матрицы А, соответствующий собственному значению А) Б) В) f(A), где f(t) любой многочлен. Найти соответствующие собственные значения этих матриц. ЛИНЕЙНЫЕ ПРОСТРАНСТВА 6.6. Является ли данное множество линейным пространством: 1. множество векторов, концы которых лежат на данной прямой; 2. множество векторов, концы которых лежат в первой четверти; 3. множество многочленов степени =3; 4. множество многочленов степени 5. множество матриц размера 2 6. множество матриц-столбцов; 7. множество натуральных чисел; 8. множество действительных чисел; 9. множество комплексных чисел; 10. множество векторов длины 1 из 11. множество всех векторов трехмерного пространства, координаты которых – целые числа; 12. множество всех векторов, являющихся линейными комбинациями векторов х, у, z; 13. множество всех четных функций a=f(t), b=g(t), заданных на отрезке [-1,+1]; сумма: 14. множество всех нечетных функций a=f(t), b=g(t), заданных на отрезке [-1,+1]; 15. множество всех линейных функций a=f 16. множество диагональных матриц; 17. множество всех невырожденных матриц; 18. множество всех симметрических матриц; 19. множество всех положительных чисел; сумма: 20. множество всех дифференцируемых функций a=f(t), b=g(t);
БАЗИС. МАТРИЦЫ ПЕРЕХОДА. ПРОЦЕСС ОРТОГОНАЛИЗАЦИИ. 7.1. Найти базис системы векторов: 1. векторов, лежащих на одной прямой; 2. на плоскости; 3. матриц второго порядка 4. многочленов степени 7.2. Найти какой-нибудь базис системы векторов: 1. 7.3. Найти координаты вектора х в базисе:
1. 2. 7.4. Найти координаты многочлена 1. в базисе: 2. в базисе: 3. в базисе: 7.5. Найти базис пространства, заданного системой линейных уравнений:
7.6. Доказать, что каждая из двух систем векторов является базисом и найти матрицу перехода от старого базиса к новому. 1.
2.
7.7. Найти координаты вектора 1.
7.8. Проверить, что векторы следующих систем попарно ортогональны, и дополнить их до ортогональных базисов: 1.
7.9. Найти векторы, дополняющие следующие системы векторов до ортонормированных базисов: 1.
7.10.Применяя процесс ортогонализации построить ортонормированный базис подпространства 1.
МАТРИЦЫ ОПЕРАТОРОВ. КВАДРАТИЧНЫЕ ФОРМЫ. МАТРИЦЫ ОПЕРАТОРОВ 8.1. Пусть оператор А поворачивает все векторы на плоскости ХОУ на угол 8.2. В пространстве а) б) 8.3. Доказать линейность и найти матрицу оператора (в базисе а) проектирования на ось ОХ; б) проектирования на плоскость z=0; в) проектирования на ось ОУ; г) проектирования на плоскость у=0; д) проектирования на плоскость 0yz; е) поворота относительно оси 0z на угол КВАДРАТИЧНЫЕ ФОРМЫ 8.5. Привести к каноническому виду квадратичную форму. Найти матрицу перехода. Выяснить знакоопределенность формы (положительно определенная, отрицательно определенная, знакопеременная) 1) 2) 3) 4) 5) 6) 7) 8)
ЧИСЛО И ВЕКТОР ФРОБЕНИУСА. ПРОДУКТИВНОСТЬ МАТРИЦ. 9.1. Найти число и вектор Фробениуса матрицы А: а) 9.2. Найти число Фробениуса матриц: а) 9.3. Продуктивна ли матрица: а) д) 9.4. При каких а) 9.5. Найти запас продуктивности матрицы: а) ВЕКТОРЫ. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ. ВЕКТОРЫ 10.1. Вычислить направляющие косинусы вектора а) б) в) 10.2. Может ли вектор составлять с координатными осями следующие углы: а) б) 10.3. Определить координаты точки М, если ее радиус вектор составляет с координатными осями одинаковые углы, а его модуль равен
10.4. По данным векторам а) 10.5. Даны: 10.6. Даны: 10.7. Проверить коллинеарность векторов а)
10.8. Проверить, что четыре точки А, В, С, Д служат вершинами трапеции: а) А(3,-1,2), В(1,2,-1), С(-1,1,-3), Д(3,-5,3). б) А(-1,5,-10), В(5,-7,8), С(2,2,-7), Д(5,-4,2). 10.9. Даны векторы 10.10. Векторы 10.11. Доказать, что если 10.12. Даны четыре вектора: СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ Проекция вектора Тогда 10.13. Векторы Найти: 1) 10.14. Доказать справедливость тождества 10.15. Установить, при каком взаимном расположении векторов 10.16. Даны единичные векторы а) б) 10.17. Дано 10.18. Какому условию должны удовлетворить векторы 10.19. Доказать, что: а) вектор б) вектор 10.20. Даны векторы Найти: 1) 5) 10.21. При каком 10.22. Найти вектор 10.23. Найти вектор х, если он перпендикулярен векторам 10.24. Даны 10.25. Найти проекцию вектора
|
||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 316; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.92.85 (0.008 с.) |

 2.
2. 
 4.
4. 
 6.
6. 

 10.
10. 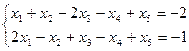
 12.
12. 
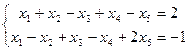 14.
14. 
 16.
16.  18.
18. 

 22.
22. 
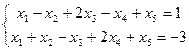 24.
24. 
 26.
26. 
 28.
28. 
 30.
30. 
 2.
2. 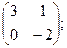 3.
3.  4.
4. 
 6.
6.  7.
7.  8.
8. 
 10.
10.  11.
11. 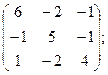 12.
12. 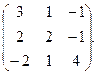

 совпадает с характеристическим многочленом матрицы А (n=3).
совпадает с характеристическим многочленом матрицы А (n=3). то х- будет собственным вектором и для:
то х- будет собственным вектором и для:
 при
при 
 3;
3; 3;
3;
 , произведение:
, произведение: 
 , b=g
, b=g  произведение
произведение  ;
; ;
;
 2.
2. 



























 в базисе
в базисе 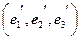 , если он задан в базисе
, если он задан в базисе  :
: 2.
2. 
 2.
2. 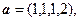


 2.
2. 



 2.
2. 
 против часовой стрелки. Найти матрицу оператора А.
против часовой стрелки. Найти матрицу оператора А.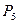 многочленов от t степени меньшей или равной 5 положим
многочленов от t степени меньшей или равной 5 положим  (оператор дифференцирования). Найти матрицу оператора в базисе:
(оператор дифференцирования). Найти матрицу оператора в базисе: ,
,  ,
,  ,
, 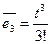 ,
,  ;
; ,
,  ,
,  .
. ):
):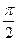 в положительном направлении.
в положительном направлении. ;
;
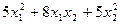





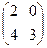 б)
б)  в)
в)  г)
г)  .
. б)
б) 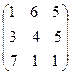 в)
в) 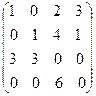 г)
г) 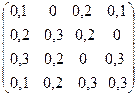 .
.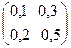 б)
б) 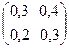 в)
в) 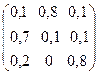 г)
г) 
 .
. матрица:
матрица: б)
б)  будет продуктивной?
будет продуктивной? б)
б)  .
. и орт вектора
и орт вектора  ):
): ;
; ;
; .
. ,
,  ,
,  ;
; ,
,  .
. .
. и
и  построить
построить ,
,  , и
, и 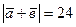 . Найти
. Найти  .
. ,
,  , и
, и 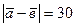 . Найти
. Найти  .
. б)
б) 


 , направленного на биссектрисе угла между векторами
, направленного на биссектрисе угла между векторами  .
. (2,6,-4) и
(2,6,-4) и  (4,2,-2) совпадают со сторонами треугольника АВС. Определить координаты векторов
(4,2,-2) совпадают со сторонами треугольника АВС. Определить координаты векторов  ,
,  и
и  , совпадающих с медианами треугольника.
, совпадающих с медианами треугольника. , лежащий в их плоскости, может быть представлен в виде:
, лежащий в их плоскости, может быть представлен в виде:  и это представление однозначно.
и это представление однозначно. ,
,  ,
,  ,
, 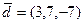 . Найти координаты каждого вектора в базисе из остальных векторов.
. Найти координаты каждого вектора в базисе из остальных векторов.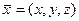 на произвольную ось
на произвольную ось 
 , где
, где  - единичный вектор на оси е.
- единичный вектор на оси е. .
. . Пусть
. Пусть  ,
,  .
. ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 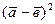 ; 5)
; 5)  ; 6)
; 6) 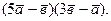
 и выяснить его геометрический смысл.
и выяснить его геометрический смысл.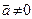 ,
, 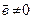 ,
,  справедливо равенство:
справедливо равенство:  .
. .
. .
. ,
,  . При каком
. При каком  и
и 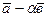 взаимно перпендикулярны?
взаимно перпендикулярны? был перпендикулярен
был перпендикулярен  ?
?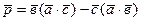 перпендикулярен к вектору
перпендикулярен к вектору  перпендикулярен к вектору
перпендикулярен к вектору 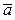 =(4,2,-1) и
=(4,2,-1) и 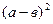 ;
; ; 6)
; 6)  ; 7)
; 7) 
 и
и  взаимно перпендикулярны?
взаимно перпендикулярны? .
. .
.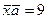 ,
,  .
.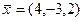 на ось, составляющую с координатными осями равные острые углы.
на ось, составляющую с координатными осями равные острые углы.


