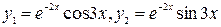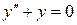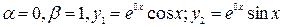Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальные уравнения 1 порядкаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте ДУ первого порядка называется уравнение, связывающее независимую переменную, искомую функцию и ее первую производную:
или в явном виде
Теорема Коши. Если в уравнении (1) функции
Геометрически это означает, что через каждую внутреннюю точку Определение. Функция y=y (x, С), зависящая от аргумента и произвольной постоянной С, называется общим решением ДУ, если 1) при любых значениях С функция y =y (x, С) является решением уравнения (1); 2) Какова бы ни была точка ДУ с разделяющимися переменными ДУ называется уравнением с разделяющимися переменными, если его можно представить в виде где правая часть есть произведение сомножителей, каждый из которых является функцией только одной переменной. Способ решения: разделение переменных по соответствующим дифференциалам (при dx должна стоять функция, зависящая от x, при dy – функция зависящая от y). Пример: 1)
2) Найти частное решение уравнения Найдем общее решение
Однородные функции Функция f(x,y) называется однородной k -ой степени однородности, если выполняется равенство:
В частности, если
Примеры 1)
2)
Однородные дифференциальные уравнения первого порядка ДУ первого порядка называется однородным, если его можно представить в виде Примеры 1)
xdy=(x+y)dx, y=xt, dy=xdt+tdx x(xdt+tdx)=(x+xt)dx xdt+tdx=(1+t)dx xdt+tdx=dx+tdx xdt=dx
2)
Пусть y=xt, dy=xdt+tdx,
- е - t =ln| x |+ C. Вернемся к старым переменным: Линейные дифференциальные уравнения первого порядка ДУ первого порядка называется линейным, если его можно представить в виде Один из способов решения – метод Бернулли (подстановка Бернулли). Будем искать решение в виде y=UV, тогда
Таким образом, решение данного линейного уравнения сводится к последовательному решению двух уравнений с разделяющимися переменными:
Тогда решение первоначального уравнения имеет вид Примеры (см. задание 4): 1) Пусть
1) 2) а)
V = cos x. б)
U = sin x + C, Тогда решение первоначального уравнения имеет вид
2)
Линейные однородные Д.У. второго порядка с постоянными Коэффициентами Это уравнения вида
где Общее решение такого уравнения имеет вид
где
Определение. Функции Решение уравнения (1) сводится к решению алгебраического уравнения
называемого характеристическим, в котором степень k равна порядку производной в уравнении (1). При этом возможны следующие случаи: 1. При Они линейно независимы (смотри определение). Тогда общее решение (1) имеет вид:
2. При
3. Если Тогда частные решения Общее решение (1) имеет вид
Примеры (см. задание 5): 1)
2)
3)
4)
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1410; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.007 с.) |


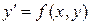
 ,
,  определены и непрерывны в некоторой области изменения переменных x и y, то какова бы ни была внутренняя точка
определены и непрерывны в некоторой области изменения переменных x и y, то какова бы ни была внутренняя точка  этой области, ДУ имеет единственное решение y=y(x), удовлетворяющее начальным условиям
этой области, ДУ имеет единственное решение y=y(x), удовлетворяющее начальным условиям
 такое, что
такое, что  – есть решение (1), удовлетворяющее начальным условиям (2).
– есть решение (1), удовлетворяющее начальным условиям (2). ,
, ;
; ;
;
 ;
; ;
; ;
; – общее решение ДУ.
– общее решение ДУ. , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям  .
.


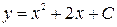 – общее решение. Выделим из него частное, удовлетворяющее начальным условиям
– общее решение. Выделим из него частное, удовлетворяющее начальным условиям  ,
,  .
. ; С =-22, тогда
; С =-22, тогда – из всего семейства интегральных кривых (парабол) выделили одну, проходящую через заданную точку (4; 2).
– из всего семейства интегральных кривых (парабол) выделили одну, проходящую через заданную точку (4; 2). .
. – функция однородная нулевой степени однородности.
– функция однородная нулевой степени однородности. .
. – однородная функция второй степени однородности.
– однородная функция второй степени однородности.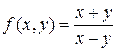 .
.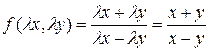 – однородная функция нулевой степени однородности.
– однородная функция нулевой степени однородности. ;
;


 , вернемся к старой переменной
, вернемся к старой переменной
 .
.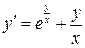





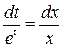
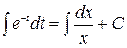 ;
; .
. , где P(x), Q(x) – заданные функции (функция y и ее производная или дифференциал dy входят в уравнение линейно, т.е. в первой степени и порознь друг от друга).
, где P(x), Q(x) – заданные функции (функция y и ее производная или дифференциал dy входят в уравнение линейно, т.е. в первой степени и порознь друг от друга). Подставим в уравнение
Подставим в уравнение 
 .Выберем V так, чтобы
.Выберем V так, чтобы  , тогда
, тогда  .
.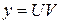
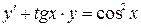 .
.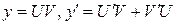 , тогда
, тогда  ,
, , сведем его к двум уравнениям
, сведем его к двум уравнениям ;
;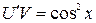 , решаем их последовательно.
, решаем их последовательно.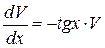


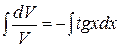
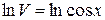 (ищем частный интеграл)
(ищем частный интеграл)



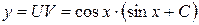 .
. ,
,  при
при  .
. ;
; ;
; 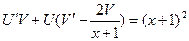 ;
;





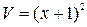







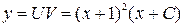 – общее решение. Выделим частное решение, удовлетворяющее начальным условиям:
– общее решение. Выделим частное решение, удовлетворяющее начальным условиям:  ;
;  ;
; 
 ,
,
 – константы.
– константы.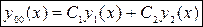
 – произвольные постоянные
– произвольные постоянные -общее решение однородного уравнения,
-общее решение однородного уравнения, -линейно независимые частные решения уравнения (1).
-линейно независимые частные решения уравнения (1). и
и  называются линейно независимыми (зависимыми) на (a, b), если при
называются линейно независимыми (зависимыми) на (a, b), если при 

 ,
,
 уравнение (2) имеет действительные различные корни
уравнение (2) имеет действительные различные корни  , тогда частные решения ДУ (1) имеют вид
, тогда частные решения ДУ (1) имеют вид  ,
,  (в чем можно убедится непосредственной подстановкой).
(в чем можно убедится непосредственной подстановкой).
 характеристическое уравнение (2) имеет два действительных равных корня
характеристическое уравнение (2) имеет два действительных равных корня 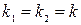 , тогда частными решениями Д.У. (1) являются функции
, тогда частными решениями Д.У. (1) являются функции  , общее решение (1) имеет вид
, общее решение (1) имеет вид
 , то характеристическое уравнение (2) не имеет действительных корней, но имеет комплексные корни вида
, то характеристическое уравнение (2) не имеет действительных корней, но имеет комплексные корни вида  .
.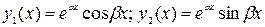

 , составим характеристическое уравнение:
, составим характеристическое уравнение: 
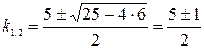 ;
;  ;
;  .
.
 , составим характеристическое уравнение
, составим характеристическое уравнение 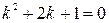
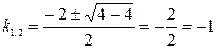 ;
; ;
; .
.