
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 1. Понятие о дифференциальном уравнении. Дифференциальные уравнения первого порядкаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Оглавление
§1. Задачи, решение которых приводит к дифференциальным уравнениям Задача 1. Остывание тела Задача 2. Движение парашюта Задача 3. Цепная линия Задача 4. Демографический процесс § 2. Основные определения Дифференциальное уравнение Обыкновенное дифференциальное уравнение Порядок дифференциального уравнения Решение (интеграл) дифференциального уравнения Интегрирование дифференциального уравнения. Общее решение дифференциального уравнения п-го порядка Частное решение дифференциального уравнения п-го порядка Интегральная кривая § 3. Дифференциальные уравнения первого порядка Дифференциальное уравнение первого порядка Уравнение первого порядка, разрешенное относительно производной Теорема о существовании и единственности решения дифференциального уравнения Задача Коши Особые точки дифференциального уравнения первого порядка Общее решением дифференциального уравнения первого порядка Частное решение дифференциального уравнения первого порядка
§ 1. Задачи, решение которых приводит к дифференциальным уравнениям
При решении многих задач математики, физики и ряда задач экономики, биологии, экологии и др. не удается установить непосредственную зависимость между искомыми и данными величинами (т.е. не удается сразу найти функцию Рассмотрим некоторые задачи, решение которых приводит к дифференциальным уравнениям. Задача 1. Остывание тела. Тело охладилось за 10 минут от 100 до 60 градусов. Температура окружающего воздуха поддерживается постоянной и равной 10 градусам. Определить, через сколько минут температура тела станет равной 20 градусам. На первый взгляд, может показаться, что эта задача решается элементарно: если тело за 10 минут охладилось на 40 градусов (100 – 60 = 40), то еще на 40 градусов (60 – 20 = 40) оно охладится также за 10 минут. Таким образом, от 100 до 20 градусов тело охладится через 20 минут. Однако такое рассуждение ошибочно. Дело в том, что, как известно из физики, скорость охлаждения тела пропорциональна разности между температурой, до которой нагрето тело, и температурой окружающей среды:
где k – коэффициент пропорциональности, подлежащий определению. Скорость охлаждения тела – это быстрота изменения его температуры, т.е. производная температуры по времени
Мы пришли к дифференциальному уравнению, которое связывает искомую функцию
Задача 2. Движение парашюта. С некоторой высоты сброшено тело, масса которого т. Требуется установить, по какому закону будет изменяться скорость v падения этого тела, если на него, кроме силы тяжести, действует тормозящая сила сопротивления воздуха, пропорциональная скорости (с коэффициентом пропорциональности k), т.е. требуется найти По второму закону Ньютона Учитывая, что ускорение есть производная скорости по времени, т.е.
Как и в первой задаче, мы пришли к дифференциальному уравнению, которое связывает искомую функцию Задача 3. Цепная линия. Гибкая однородная нить подвешена за два конца. Найти уравнение кривой, по которой расположится нить под действием
Зная, что
Продифференцируем обе части равенства по х:
Из аналитической геометрии известно, что
Полученное дифференциальное уравнение выражает связь между первой и второй производными от некоторой функции у. Его решение есть уравнение цепной линии.
Задача 4. Демографический процесс. Из статистических данных известно, что для рассматриваемого региона число новорожденных и число умерших за единицу времени пропорционально численности населения с коэффициентами пропорциональности соответственно k 1 и k 2. Найти закон изменения численности населения с течением времени (описать протекание демографического процесса). Пусть Прирост населения Δ у за время Δ t равен разности между числом родившихся и числом умерших за это время, т.е. Поделим обе части уравнения на Δ t и обозначим k 1 – k 2 = k, получим:
Переходя к пределу при Δ t → 0, имеем
Учитывая, что
Как видим, в процессе решения приведенных выше задач, мы всегда приходим к дифференциальным уравнениям. Изучению методов решения различных видов дифференциальных уравнений будут посвящены наши дальнейшие занятия.
§ 2. Основные определения
Дифференциальным уравнением (ДУ) называется уравнение, связывающее независимую переменную x, искомую функцию Символически дифференциальное уравнение можно записать так:
или
Если искомая функция Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение. Так, например, уравнение Решением или интегралом дифференциального уравнения называется всякая функция Например, функция В самом деле, Нетрудно доказать, что и функция Вообще все функции вида Дифференциальное уравнение имеет бесчисленное множество решений. Т.к. при решении дифференциальных уравнений часто приходится выполнять операцию интегрирования, то процесс нахождения решения дифференциального уравнения называют интегрированием дифференциального уравнения. Общим решением дифференциального уравнения п -го порядка называется такое его решение Частным решением дифференциального уравнения п -го порядка называется решение, получаемое из общего решения при некоторых конкретных числовых значениях постоянных С 1, С 2, …, Сп. Для нахождения частного решения дифференциального уравнения п -го порядка в общем случае требуется задать п дополнительных начальных условий. Например, уравнение График решения дифференциального уравнения называется интегральной кривой. Т.к. дифференциальное уравнение имеет бесчисленное множество решений, то и интегральных кривых для конкретного дифференциального уравнения существует бесчисленное множество. Общему решению дифференциального уравнения соответствует семейство кривых на координатной плоскости, зависящее от произвольных постоянных С 1, С 2, …, Сп. Например, интегральными кривыми дифференциального уравнения (из примера, приведенного выше)
Рис.2. Частному решению дифференциального уравнения соответствует какая-то одна кривая из семейства, полученная при конкретных значениях произвольных постоянных С 1, С 2, …, Сп.
§ 3. Дифференциальные уравнения первого порядка.
Дифференциальное уравнение первого порядка связывает независимую переменную, искомую функцию и ее первую производную. В общем виде его можно записать так
Здесь x – независимая переменная, Дифференциальное уравнение первого порядка может не содержать в явном виде x и Дифференциальное уравнение первого порядка, которое может быть представлено в виде Для такого уравнения справедлива следующая теорема. Теорема о существовании и единственности решения ДУ. Если в уравнении Геометрический смысл теоремы заключается в том, что существует и притом единственная интегральная кривая, которая проходит через точку (х 0; у 0). Нахождение решения уравнения Точки плоскости Оху, в которых не выполняются условия теоремы существования и единственности решения дифференциального уравнения, называются особыми точками дифференциального уравнения. В этих точках терпит разрыв или сама функция Общим решением дифференциального уравнения первого порядка называется функция 1) она является решением этого дифференциального уравнения при любом конкретном значении постоянной С; 2) какова бы ни была точка (х 0; у 0), лежащая внутри области D, существует единственное значение постоянной С = С 0 такое, что решение Значение С 0 можно найти из уравнения Частным решением дифференциального уравнения первого порядка называется любая функция С методами решения различных видов дифференциальных уравнений первого порядка мы познакомимся на следующем занятии. Дифференциальные уравнения
|
||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 979; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.01 с.) |

 ), но зато удается составить уравнение, связывающее независимую переменную, искомую функцию и ее производные. Такое уравнение называется дифференциальным. Оно может не содержать в явном виде независимую переменную и искомую функцию, но обязательно должно содержать одну или несколько производных искомой функции.
), но зато удается составить уравнение, связывающее независимую переменную, искомую функцию и ее производные. Такое уравнение называется дифференциальным. Оно может не содержать в явном виде независимую переменную и искомую функцию, но обязательно должно содержать одну или несколько производных искомой функции. ,
, . Учитывая, что по условию задачи Т среды = 10 градусов и постоянна, получим
. Учитывая, что по условию задачи Т среды = 10 градусов и постоянна, получим .
. и ее производную
и ее производную  и не содержит в явном виде независимую переменную. При решении этого уравнения, следует учитывать, что искомая функция должна удовлетворять следующим требованиям, указанным в задаче: в начальный момент времени t = 0 температура тела Т = 100 градусов; при t = 10 (минут) температура тела Т = 60 градусов.
и не содержит в явном виде независимую переменную. При решении этого уравнения, следует учитывать, что искомая функция должна удовлетворять следующим требованиям, указанным в задаче: в начальный момент времени t = 0 температура тела Т = 100 градусов; при t = 10 (минут) температура тела Т = 60 градусов. .
. , где а – ускорение движущегося тела, а F – сила, действующая на тело в направлении движения. Эта сила складывается из двух: силы тяжести
, где а – ускорение движущегося тела, а F – сила, действующая на тело в направлении движения. Эта сила складывается из двух: силы тяжести 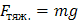 и силы сопротивления воздуха
и силы сопротивления воздуха  (берем ее с отрицательным знаком, т.к. она направлена в сторону, противоположную направлению скорости).
(берем ее с отрицательным знаком, т.к. она направлена в сторону, противоположную направлению скорости). , получим:
, получим: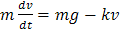 .
. и ее производную
и ее производную  и не содержит в явном виде независимую переменную. Это уравнение движения некоторых типов парашютов.
и не содержит в явном виде независимую переменную. Это уравнение движения некоторых типов парашютов. ,
где φ – угол между осью Ох и касательной к искомой линии,
s – длина дуги,
γ – линейный удельный вес нити,
Н – натяжение нити.
,
где φ – угол между осью Ох и касательной к искомой линии,
s – длина дуги,
γ – линейный удельный вес нити,
Н – натяжение нити.
 Рис.1.
Рис.1.
 (геометрический смысл производной) и обозначив через а отношение
(геометрический смысл производной) и обозначив через а отношение  , получим
, получим .
. .
. . Тогда получим:
. Тогда получим: или
или 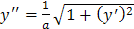 .
. – число жителей региона в момент времени t, тогда число новорожденных за единицу времени равно
– число жителей региона в момент времени t, тогда число новорожденных за единицу времени равно  , а число умерших за единицу времени равно
, а число умерших за единицу времени равно  . В этом случае за время Δ t число родившихся равно
. В этом случае за время Δ t число родившихся равно  , а число умерших –
, а число умерших – 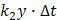 .
. .
.

 и
и  получаем дифференциальное уравнение:
получаем дифференциальное уравнение:  , которое является математической моделью демографического процесса. Решение этого уравнения и будет законом изменения численности населения с течением времени.
, которое является математической моделью демографического процесса. Решение этого уравнения и будет законом изменения численности населения с течением времени. .
.

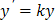 из Задачи 4 есть уравнение первого порядка, а уравнение
из Задачи 4 есть уравнение первого порядка, а уравнение  из Задачи 3 – уравнение второго порядка.
из Задачи 3 – уравнение второго порядка. , которая, будучи подставлена в уравнение, превращает его в тождество.
, которая, будучи подставлена в уравнение, превращает его в тождество. является решением дифференциального уравнения
является решением дифференциального уравнения  .
. , тогда
, тогда  .
. также является решением этого дифференциального уравнения.
также является решением этого дифференциального уравнения. , где С 1 и С 2 – произвольные постоянные являются решением данного дифференциального уравнения.
, где С 1 и С 2 – произвольные постоянные являются решением данного дифференциального уравнения. , которое является функцией переменной х и п произвольных независимых постоянных С 1, С 2, …, Сп.
, которое является функцией переменной х и п произвольных независимых постоянных С 1, С 2, …, Сп. – это общее решение дифференциального уравнения
– это общее решение дифференциального уравнения  . При начальном условии у (0) = 1, получим, что С = 1, а значит соответствующее частное решение имеет вид
. При начальном условии у (0) = 1, получим, что С = 1, а значит соответствующее частное решение имеет вид  .
.
 .
.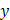 – искомая функция, и
– искомая функция, и  – ее производная.
– ее производная. , называется уравнением первого порядка, разрешенным относительно производной.
, называется уравнением первого порядка, разрешенным относительно производной. и ее частная производная по у непрерывны в некоторой области D на плоскости Оху, содержащей некоторую точку (х 0; у 0), то существует единственное решение этого уравнения
и ее частная производная по у непрерывны в некоторой области D на плоскости Оху, содержащей некоторую точку (х 0; у 0), то существует единственное решение этого уравнения  , удовлетворяющее условию: при х = х 0 у = у0.
, удовлетворяющее условию: при х = х 0 у = у0. , удовлетворяющего начальному условию у (х 0) = у0, называется задачей Коши.
, удовлетворяющего начальному условию у (х 0) = у0, называется задачей Коши. . Через каждую из таких точек может проходить либо несколько интегральных кривых, либо не проходит ни одной.
. Через каждую из таких точек может проходить либо несколько интегральных кривых, либо не проходит ни одной. , которая зависит от одной произвольной постоянной и удовлетворяет условиям:
, которая зависит от одной произвольной постоянной и удовлетворяет условиям: удовлетворяет начальному условию у (х 0) = у0.
удовлетворяет начальному условию у (х 0) = у0. .
.


