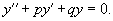Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные однородные дифференциальные уравнения 2-го порядкаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
5)Линейные неоднородные дифференциальные уравнения 2-ого порядка:
26) Дифференциальные уравнения с разделяющимися переменными:
В дифференциальных уравнениях
Пример. Решить уравнение: Разделяем переменные:
Интегрируя, получаем Далее из уравнений
27) Однородные дифференциальные уравнения 1-го порядка:
Однородным дифференциальным уравнением первого порядка, называется уравнение, имеющее вид
Уравнение 1-го порядка
28) Линейные уравнения первого порядка:
Уравнение вида: y'+p(x)у=q(х) (10) где р(х) и q(х) — непрерывные функции, называется линейным дифференциальным уравнением первого порядка. Название уравнения объясняется тем, что неизвестная функция у и ее производная у' входят в уравнение линейно, т. е. в первой степени. ОПРЕДЕЛЕНИЕ. Если q(х) = 0, то уравнение (10) называется линейным однородным уравнением. Если q(х)≠0, то уравнение (10) называется линейным неоднородным уравнением.
Теорема о структуре общего решения линейного неоднородного уравнения: Если все коэффициенты уравнения линейного однородного дифференциального уравнениния непрерывны на отрезке [a;b], а функции y1(x), y2(x),..., y n (x) образуют систему решений соответствующего однородного уравнения, то общее решение неоднородного уравнения имеет вид y(x,C1,..., C n) = C1 y1(x) + C2 y2(x) +... + C n yn (x) + y *(x), где C1,...,C n — произвольные постоянные, y *(x) — частное решение неоднородного уравнения. Метод Лагранжа (метод вариации произвольных постоянных) — метод для получения общего решения неоднородного уравнения, зная общее решение однородного уравнения без нахождения частного решения.
29) Дифференциальные уравнения второго порядка: Дифференциальное уравнение второго порядка можно записать в виде
Для этих уравнений имеет место теорема существования и единственности решения. Теорема. Если в уравнении Общим решением дифференциального уравнения второго порядка называется функция Если в общее решение подставить конкретные значения Задача Коши для дифференциального уравнения 2-го порядка (1.1) состоит в отыскании частного решения уравнения, удовлетворяющего начальным условиям: при 30) Линейные однородные дифференциальные уравнения 2-го порядка:
Линейным однородным уравнением второго порядка называется уравнение Уравнение
Определителем Вронского W(x; y 1(x), y 2(x),..., yn (x)) называется определитель, первая строка которого образована функциями y 1(x), y 2(x),..., yn (x) из C n -1[ a, b ], а последующие строки образованы производными от функций предыдущей строки:
Справедливо следующее необходимое условие линейной зависимости функций. Если функции y 1(x), y 2(x),..., yn (x) линейно зависимы на отрезке [a;b], то их определитель Вронского тождественно равен нулю на этом отрезке: W(x; y 1(x), y 2(x),..., yn (x)) ≡ 0 на [a;b]. Другими словами, функции y 1(x), y 2(x), …, yn (x) линейно зависимы на интервале (a, b), если существует равная нулю на (a, b) их нетривиальная линейная комбинация. Функции y 1(x), y 2(x), …, yn (x) линейно независимы на интервале (a, b), если только тривиальная их линейная комбинация тождественно равна нулю на (a, b).
31) Линейные неоднородные дифференциальные уравнения 2-го порядка:
Линейное неоднородное уравнение данного типа имеет вид:
где p, q − постоянные числа (которые могут быть как действительными, так и комплексными). Для каждого такого уравнения можно записать соответствующее однородное уравнение:
Теорема: Общее решение неоднородного уравнения является суммой общего решения y 0(x) однородного уравнения и частного решения y 1(x) неоднородного уравнения:
Ниже мы рассмотрим два способа решения неоднородных дифференциальных уравнений.
Метод вариации постоянных Если общее решение y 0 однородного уравнения известно, то общее решение неоднородного уравнения можно найти, используя метод вариации постоянных. Пусть общее решение однородного дифференциального уравнения второго порядка имеет вид:
Вместо постоянных C 1 и C 2 будем рассматривать вспомогательные функции C 1(x) и C 2(x). Будем искать эти функции такими, чтобы решение
удовлетворяло неоднородному уравнению с правой частью f (x).
|
||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 635; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.158.110 (0.011 с.) |

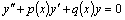

 .
.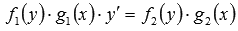 переменные могут быть разделены, проведением преобразований. Такие ОДУ называются дифференциальными уравнениями с разделяющимися переменными. Соответствующее ДУ с разделенными переменными запишется как
переменные могут быть разделены, проведением преобразований. Такие ОДУ называются дифференциальными уравнениями с разделяющимися переменными. Соответствующее ДУ с разделенными переменными запишется как  .
.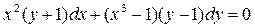 .
.
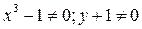 .
.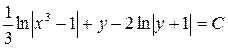
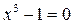 и
и  находим X=1, Y=-1. Эти решения – частные решения.
находим X=1, Y=-1. Эти решения – частные решения.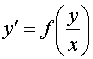 (7)
(7) называется однородным, если для его правой части при любых
называется однородным, если для его правой части при любых  справедливо соотношение
справедливо соотношение 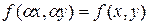 , называемое условием однородности функции двух переменных нулевого измерения.
, называемое условием однородности функции двух переменных нулевого измерения. . Мы будем рассматривать уравнения второго порядка, которые можно разрешить относительно производной второго порядка, то есть записать в виде
. Мы будем рассматривать уравнения второго порядка, которые можно разрешить относительно производной второго порядка, то есть записать в виде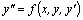 .
. и ее частные производные по аргументам y и
и ее частные производные по аргументам y и 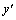 непрерывны в некоторой области, содержащей
непрерывны в некоторой области, содержащей 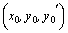 , то существует единственное решение
, то существует единственное решение 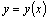 уравнения, удовлетворяющее условиям
уравнения, удовлетворяющее условиям 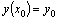 и
и 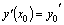 .
.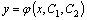 , зависящая от двух произвольных постоянных, которая при любых значениях
, зависящая от двух произвольных постоянных, которая при любых значениях 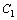 и
и 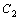 является решением дифференциального уравнения.
является решением дифференциального уравнения.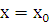 :
:  ,
, 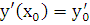 . Однако решение задачи Коши для уравнений 2-го порядка (1.1) при довольно широких предположениях для функций, входящих в уравнение,единственно, т.е. всякие два решения с общим начальным условием
. Однако решение задачи Коши для уравнений 2-го порядка (1.1) при довольно широких предположениях для функций, входящих в уравнение,единственно, т.е. всякие два решения с общим начальным условием  и
и  постоянны, т.е. не зависят от
постоянны, т.е. не зависят от 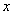 , то это уравнение называют уравнением с постоянными коэффициентами и записывают его так:
, то это уравнение называют уравнением с постоянными коэффициентами и записывают его так: 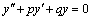 .
. , которое получается из линейного однородного уравнения заменой функции
, которое получается из линейного однородного уравнения заменой функции 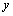 единицей, а
единицей, а 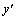 и
и 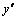 - соответствующими степенями
- соответствующими степенями 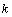 , называется характеристическим уравнением.
, называется характеристическим уравнением.