
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Если поменять местами верхний и нижний пределы интегрирования, то определённый интеграл изменит знакСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Не от всякой иррациональной функции интеграл выражается через элементарные функции. Рассмотрим те функции, интегралы от которых с помощью подстановок приводятся к интегралам от рациональных функций и интегрируются в элементарных функциях. Пример. Вычислить интеграл Решение. Выполним подстановку 10) Нахождение площади криволинейной трапеции: Пусть на отрезке [a,b] задана непрерывная функция y=F(x)>=0. Фигура, ограниченная сверху графиком функции y=f(x), снизу – осью Ох, сбоку – прямыми x=a и x=b, называется криволинейной трапецией.
Произведение
Нахождение работы переменной силы: Пусть точка движется по оси Ох под действием силы, проекция которой на ось Ох есть функция f от х. При этом мы будем предполагать, что f есть непрерывная функция. Под действием этой силы материальная точка переместилась из точки М (а) в точку М (b) (рис. 1, а). Покажем, что в этом случае работа А подсчитывается по формуле
Работа силы на всем отрезке [а; b] равна сумме работ этой силы на полученных отрезках. Точность приближенного равенства тем выше, чем короче отрезки, на которые разбит отрезок [а;b] Естественно, что это приближенное равенство переходит в точное, если считать, что n→∞:
Следовательно работа переменной силы F, величина которой есть непрерывная функция F = F(x), действующей на отрезке [a,b], равна определенному интегралу от величины F(x) силы, взятому по отрезку [а,b]
11) Определенный интеграл: 1. С помощью точек х0=а, x1, х2,..., хn = В (х0 <x1 <...< хn) разобьем отрезок [а, b] на n частичных отрезков [х0;х1], [x1; х2],..., [хn-1,хn] 2. В каждом частичном отрезке [xi-1;xi], i = 1,2,...,n выберем произвольную точку сi є [xi-1; xi] и вычислим значение функции в ней, т. е. величину ƒ(сi). 3. Умножим найденное значение функции ƒ (сi) на длину ∆xi=xi-xi-1 соответствующего частичного отрезка: ƒ (сi) • ∆хi. 4. Составим сумму Sn всех таких произведений:
Сумма вида (35.1) называется интегральной суммой функции у = ƒ(х) на отрезке [а; b]. Если при этом интегральная сумма Sn имеет предел I, который не зависит ни от способа разбиения отрезка [а; b] на частичные отрезки, ни от выбора точек в них, то число I называется определенным интегралом от функции у = ƒ(х) на отрезке [а; b] и обозначается
Геометрический смысл: Геометрический смысл определенного интеграла заключается в том, что определенный интеграл равен площади криволинейной трапеции, прилегающей к оси Ox и ограниченной кривой у=f(x) Если f (x) непрерывна и положительна на [ a, b ], то интеграл
Пусть на отрезке [a,b] задана непрерывная функция y=F(x)>=0. Фигура, ограниченная сверху графиком функции y=f(x), снизу – осью Ох, сбоку – прямыми x=a и x=b, называется криволинейной трапецией.
Условия существования определенного интеграла: Если бы функция f(x) была в промежутке [a, b] неограниченна, то – при любом разбиении промежутка на части – она сохранила бы подобное свойство хоть в одной из частей. 12) Свойства определенного интеграла: 1)Линейность. Если функции y = f (x), y = g (x) интегрируемы по отрезку [ a, b ], то по этому отрезку интегрируема их линейная комбинация A f (x) + B g (x) (A, B = const), и 2)Аддитивность. Если y = f (x) интегрируема по отрезку [ a, b ] и точка c принадлежит этому отрезку, то
3)Интеграл от единичной функции (f (x) = 1). Если f (x) = 1, то Теорема 7.3. Объем тела вращения равен
Теорема 7.4. Объем шара равен Доказательство В качестве тренировки докажите, что объем эллипсоида, задаваемого уравнением
22) Длина дуги плоской кривой в декартовых и полярных:
Пусть плоская кривая АВ задана уравнением у = f (x), a ≤ x ≤ b, где f (x) – непрерывная вместе со своей производной на отрезке [ а, b ] функция. Разобьем кривую АВ на n произвольных частей точками А = М 0, М 1, М 2, …, M i - 1, M i , …, Mn = B в направлении от А к В. Соединив эти точки хордами, получим некоторую вписанную ломанную линию, длину которой обозначим через Р.
Определение. Число L называется пределом длин ломаных Р при μ → 0, если для любого как угодно малого ε > 0 существует δ > 0 такое, что для всякой ломаной, у которой μ < δ, выполняется неравенство | L − P | < ε.
Если функция f (x) непрерывна вместе с f ' (x) на отрезке [ а, b ], то длина дуги АВ выражается формулой
23) Несобственные интегралы: Определённый интеграл называется несобственным, если выполняется, по крайней мере, одно из следующих условий:
Пусть функция f (x) непрерывна при a ≤ x < +∞. Тогда по определению полагают
Если предел (2) существует, то несобственный интеграл с бесконечным пределом интегрирования, стоящий в левой части равенства (2), назвается сходящимся и его значение определяется формулой (2); в противном случае равенство (2) теряет смысл, несобственный интеграл, стоящий слева, называется расходящимся и ему не приписывается никакого числового значения.. Пример:
24) Несобственные интегралы от неограниченных функций: Пусть функция f(x) определена и неограничена на полуинтервале [а, b), при этом она ограничена и интегрируема на любом отрезке [а, с], где а
Особенность на левом конце промежутка интегрирования. Пусть функция f (x) определена на полуинтервале (a, b ], интегрируема по любому отрезку
Несобственным интегралом от f (x) по отрезку [ a, b ] называется предел Особенность на правом конце промежутка интегрирования. Пусть функция f (x) определена на полуинтервале [ a, b), интегрируема по любому отрезку Несобственным интегралом от f (x) по отрезку [ a, b ] называется предел 25) Дифференциальные уравнения: Дифференциа́льное уравне́ние — уравнение, связывающее значение некоторой неизвестной функции в некоторой точке и значение её производных различных порядков в той же точке. Стоит также отметить, что дифференциальное уравнение может вообще не содержать неизвестную функцию, некоторые её производные и свободные переменные, но обязано содержать хотя бы одну из производных. Виды уравнений: 1) Обыкновенные дифференциальные уравнения (ОДУ) — это уравнения вида
2) Дифференциальные уравнения с разделяющимися переменными вида 3) Линейные неоднородные дифференциальные уравнения первого порядка Метод вариации постоянных Если общее решение y 0 однородного уравнения известно, то общее решение неоднородного уравнения можно найти, используя метод вариации постоянных. Пусть общее решение однородного дифференциального уравнения второго порядка имеет вид:
Вместо постоянных C 1 и C 2 будем рассматривать вспомогательные функции C 1(x) и C 2(x). Будем искать эти функции такими, чтобы решение
удовлетворяло неоднородному уравнению с правой частью f (x).
Метод вариации постоянных Если общее решение y 0 однородного уравнения известно, то общее решение неоднородного уравнения можно найти, используя метод вариации постоянных. Пусть общее решение однородного дифференциального уравнения второго порядка имеет вид:
Вместо постоянных C 1 и C 2 будем рассматривать вспомогательные функции C 1(x) и C 2(x). Будем искать эти функции такими, чтобы решение
удовлетворяло неоднородному уравнению с правой частью f (x).
36). Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами и правой частью вида f(x)= P(x)eax, где P(x)- многочлен:
Линейное неоднородное уравнение данного типа имеет вид:
где p, q − постоянные числа (которые могут быть как действительными, так и комплексными). Для каждого такого уравнения можно записать соответствующее однородное уравнение:
Теорема: Общее решение неоднородного уравнения является суммой общего решения y 0(x) соответствуюшего однородного уравнения и частного решения y 1(x) неоднородного уравнения:
Умножение матрицы на число Произведением матрицы Транспонирование матрицы:
Если в данной матрице поменять строки и столбцы местами, то получится транспонированная матрица данной. Например, дана матрица М, каждую строчку этой матрицы перенесем в соответствующий столбец матрицы, стоящей на рисунке рядом. Вторая матрица - это транспонированная матрица матрицы М. 39) Определитель квадратной матрицы: Определи́тель —является многочленом от элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равно). В общем случае матрица может быть определена над любым коммутативным кольцом, в этом случае определитель будет элементом того же кольца.Определитель матрицы А обозначается как: det(A), |А| или Δ(A).
Свойства определителя: 1)Если поменять местами два параллельных ряда, то определитель изменит знак. 2)Определитель не изменится, если к элементам любого ряда прибавить элементы параллельного ряда, предварительно умноженные на одно и то же число. 3)Определитель равен сумме произведений элементов любого ряда на их алгебраические дополнения. 4)Определитель с двумя одинаковыми параллельными рядами равен нулю.
5)Определитель с нулевым рядом равен нулю. 6)Определитель треугольного вида равен произведению диагональных элементов. 7)Определитель не меняется при транспонировании. 8)Общий множитель можно вынести за знак определителя. Орт вектора Ортом вектора
Модуль вектора (длина вектора) |a| в прямоугольных декартовых координатах равен квадратному корню из суммы квадратов его координат. Так в случае плоской задачи модуль вектора
Не от всякой иррациональной функции интеграл выражается через элементарные функции. Рассмотрим те функции, интегралы от которых с помощью подстановок приводятся к интегралам от рациональных функций и интегрируются в элементарных функциях. Пример. Вычислить интеграл Решение. Выполним подстановку 10) Нахождение площади криволинейной трапеции: Пусть на отрезке [a,b] задана непрерывная функция y=F(x)>=0. Фигура, ограниченная сверху графиком функции y=f(x), снизу – осью Ох, сбоку – прямыми x=a и x=b, называется криволинейной трапецией.
Произведение
Нахождение работы переменной силы: Пусть точка движется по оси Ох под действием силы, проекция которой на ось Ох есть функция f от х. При этом мы будем предполагать, что f есть непрерывная функция. Под действием этой силы материальная точка переместилась из точки М (а) в точку М (b) (рис. 1, а). Покажем, что в этом случае работа А подсчитывается по формуле
Работа силы на всем отрезке [а; b] равна сумме работ этой силы на полученных отрезках. Точность приближенного равенства тем выше, чем короче отрезки, на которые разбит отрезок [а;b] Естественно, что это приближенное равенство переходит в точное, если считать, что n→∞:
Следовательно работа переменной силы F, величина которой есть непрерывная функция F = F(x), действующей на отрезке [a,b], равна определенному интегралу от величины F(x) силы, взятому по отрезку [а,b]
11) Определенный интеграл: 1. С помощью точек х0=а, x1, х2,..., хn = В (х0 <x1 <...< хn) разобьем отрезок [а, b] на n частичных отрезков [х0;х1], [x1; х2],..., [хn-1,хn] 2. В каждом частичном отрезке [xi-1;xi], i = 1,2,...,n выберем произвольную точку сi є [xi-1; xi] и вычислим значение функции в ней, т. е. величину ƒ(сi). 3. Умножим найденное значение функции ƒ (сi) на длину ∆xi=xi-xi-1 соответствующего частичного отрезка: ƒ (сi) • ∆хi. 4. Составим сумму Sn всех таких произведений:
Сумма вида (35.1) называется интегральной суммой функции у = ƒ(х) на отрезке [а; b]. Если при этом интегральная сумма Sn имеет предел I, который не зависит ни от способа разбиения отрезка [а; b] на частичные отрезки, ни от выбора точек в них, то число I называется определенным интегралом от функции у = ƒ(х) на отрезке [а; b] и обозначается
Геометрический смысл: Геометрический смысл определенного интеграла заключается в том, что определенный интеграл равен площади криволинейной трапеции, прилегающей к оси Ox и ограниченной кривой у=f(x) Если f (x) непрерывна и положительна на [ a, b ], то интеграл
Пусть на отрезке [a,b] задана непрерывная функция y=F(x)>=0. Фигура, ограниченная сверху графиком функции y=f(x), снизу – осью Ох, сбоку – прямыми x=a и x=b, называется криволинейной трапецией.
Условия существования определенного интеграла: Если бы функция f(x) была в промежутке [a, b] неограниченна, то – при любом разбиении промежутка на части – она сохранила бы подобное свойство хоть в одной из частей. 12) Свойства определенного интеграла: 1)Линейность. Если функции y = f (x), y = g (x) интегрируемы по отрезку [ a, b ], то по этому отрезку интегрируема их линейная комбинация A f (x) + B g (x) (A, B = const), и 2)Аддитивность. Если y = f (x) интегрируема по отрезку [ a, b ] и точка c принадлежит этому отрезку, то
3)Интеграл от единичной функции (f (x) = 1). Если f (x) = 1, то Если поменять местами верхний и нижний пределы интегрирования, то определённый интеграл изменит знак
13)Теорема об оценке интеграла: 5.1. Если на отрезке [ a, b ] функция удовлетворяет неравенству
14) Теорема о среднем значении для определенного интеграла: Если f (x) непрерывна на отрезке [ a, b ], то существует точка Это свойство имеет простую геометрическую интерпретацию: если
15) Интеграл с переменным верхним пределом. Значение определённого интеграла не зависит от того, какой буквой обозначена переменная интегрирования:
Если функция f (t) непрерывна в окрестности точки t = x, то в этой точке функция Ф(x) дифференцируема, и
16) Формула Ньютона-Лейбница: Даёт соотношение между операциями взятия определенного интеграла и вычисления первообразной. Формула Ньютона-Лейбница - основная формула интегрального исчисления.
Данная формула верна для любой функции f(x), непрерывной на отрезке [а, b], F - первообразная для f(x). Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f(x), вычислить ее значения в точках a и b и найти разность F(b) – F(a).
17) Замена переменной в определенном интеграле:
ТЕОРЕМА. Пусть функция φ(t) имеет непрерывную производную на отрезке [α,β], а=φ(α), в=φ(β) и функция f(х) непрерывна в каждой точке х вида х=φ(t), где t Тогда справедливо следующее равенство:
Эта формула носит название формулы замены переменной в определенном интеграле. Пример.Вычислить Воспользуемся заменой переменной
18) Интегрирование по частям в определенном интеграле:
Если функции u=u(x) и v=v(x) имеют непрерывные производные на отрезке [ a, b ], то справедлива формула интегрирования по частям:
Пример:
Для нахождения полученного интеграла положим 1+х=t. Тогда dx=dt, x=t-1 и если х=0, то t=1, если x=1, то t=2. Следовательно,
19) Полярная система координат:
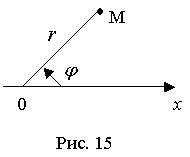
Полярная система координат — двухмерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом Возьмем на плоскости направленную прямую Ох и на ней точку О (рис. 15).
Положение точки М на этой плоскости определяется двумя числами: ее расстоянием r от взятой нами точки О и углом φ, образуемым отрезком ОМ с положительным направлением прямой Ох. Числа r и φ называются полярными координатами точки М, причем r называется радиус-вектором, Прямая Ох называется полярной осью, а точка О - полюсом полярной системы координат. Заметим, что r (как расстояние) - всегда величина положительная, а угол φ может изменяться от 0 до 2π и далее до бесконечности.
20)Вычисление площади плоской фигуры с помощью определенного интеграла в декартовой, полярной системах координат.
21). Объем тела вращения: Укажем общий способ вычисления объемов тел вращения. В частности, вычислим объем шара и его частей. Пусть криволинейная трапеция, то есть фигура, ограниченная осью Ox, прямыми x = a, x = b и графиком непрерывной возрастающей неотрицательной функции y = f (x), вращается вокруг оси Ox (рис. 7.2.1), вследствие чего образуется тело вращения. Объем части тела вращения, ограниченной сечениями, проведенными через точки a и x, обозначим через V (x), а объем данного тела вращения – через V. Теорема 7.3. Объем тела вращения равен
Теорема 7.4. Объем шара равен Доказательство В качестве тренировки докажите, что объем эллипсоида, задаваемого уравнением
22) Длина дуги плоской кривой в декартовых и полярных:
Пусть плоская кривая АВ задана уравнением у = f (x), a ≤ x ≤ b, где f (x) – непрерывная вместе со своей производной на отрезке [ а, b ] функция. Разобьем кривую АВ на n произвольных частей точками А = М 0, М 1, М 2, …, M i - 1, M i , …, Mn = B в направлении от А к В. Соединив эти точки хордами, получим некоторую вписанную ломанную линию, длину которой обозначим через Р. Определение. Число L называется пределом длин ломаных Р при μ → 0, если для любого как угодно малого ε > 0 существует δ > 0 такое, что для всякой ломаной, у которой μ < δ, выполняется неравенство | L − P | < ε.
Если функция f (x) непрерывна вместе с f ' (x) на отрезке [ а, b ], то длина дуги АВ выражается формулой
23) Несобственные интегралы: Определённый интеграл называется несобственным, если выполняется, по крайней мере, одно из следующих условий:
Пусть функция f (x) непрерывна при a ≤ x < +∞. Тогда по определению полагают
Если предел (2) существует, то несобственный интеграл с бесконечным пределом интегрирования, стоящий в левой части равенства (2), назвается сходящимся и его значение определяется формулой (2); в противном случае равенство (2) теряет смысл, несобственный интеграл, стоящий слева, называется расходящимся и ему не приписывается никакого числового значения.. Пример:
24) Несобственные интегралы от неограниченных функций: Пусть функция f(x) определена и неограничена на полуинтервале [а, b), при этом она ограничена и интегрируема на любом отрезке [а, с], где а
Особенность на левом конце промежутка интегрирования. Пусть функция f (x) определена на полуинтервале (a, b ], интегрируема по любому отрезку
Несобственным интегралом от f (x) по отрезку [ a, b ] называется предел Особенность на правом конце промежутка интегрирования. Пусть функция f (x) определена на полуинтервале [ a, b), интегрируема по любому отрезку Несобственным интегралом от f (x) по отрезку [ a, b ] называется предел 25) Дифференциальные уравнения: Дифференциа́льное уравне́ние — уравнение, связывающее значение некоторой неизвестной функции в некоторой точке и значение её производных различных порядков в той же точке. Стоит также отметить, что дифференциальное уравнение может вообще не содержать неизвестную функцию, некоторые её производные и свободные переменные, но обязано содержать хотя бы одну из производных. Виды уравнений: 1) Обыкновенные дифференциальные уравнения (ОДУ) — это уравнения вида
2) Дифференциальные уравнения с разделяющимися переменными вида 3) Линейные неоднородные дифференциальные уравнения первого порядка
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 920; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.83.45 (0.014 с.) |

 .
. ,
, 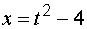 ,
,  , тогда
, тогда
 (рис.),
(рис.), 
 .
. 
 даст площадь прямоугольника, имеющего основание
даст площадь прямоугольника, имеющего основание  и высоту
и высоту  , а сумма
, а сумма 

 (1)
(1)
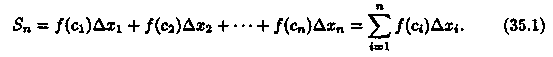
 Таким образом,
Таким образом,



 .
. .
. .
.
 где R – радиус шара.
где R – радиус шара. определяется формулой
определяется формулой
 .
.



 (2)
(2)
 с Если существует конечный предел
с Если существует конечный предел  , то он называется несобственным интегралом функции f(x) на отрезке [а, b] и обозначается
, то он называется несобственным интегралом функции f(x) на отрезке [а, b] и обозначается
 , и имеет бесконечный предел при
, и имеет бесконечный предел при  .
. . Если этот предел конечен, говорят, что интеграл сходится; если предел не существует или бесконечен, говорят, что интеграл расходится.
. Если этот предел конечен, говорят, что интеграл сходится; если предел не существует или бесконечен, говорят, что интеграл расходится. , и имеет бесконечный предел при
, и имеет бесконечный предел при  .
. . Если этот предел конечен, говорят, что интеграл сходится; если предел не существует или бесконечен, говорят, что интеграл расходится.
. Если этот предел конечен, говорят, что интеграл сходится; если предел не существует или бесконечен, говорят, что интеграл расходится. или
или  ,
,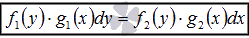 или
или 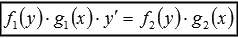 .
. .
.


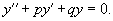

 на число
на число 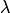 называется матрица
называется матрица  тех же размеров, что и матрица
тех же размеров, что и матрица  , каждый элемент которой равен произведению числа
, каждый элемент которой равен произведению числа 
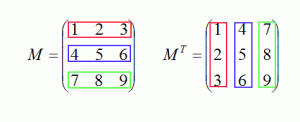

 называется вектор единичной длины, имеющий то же направление, что и вектор
называется вектор единичной длины, имеющий то же направление, что и вектор  .
.







 можно найти по следующей формуле
можно найти по следующей формуле
 .
.
 , то
, то  .
.  .
. , такая что
, такая что  .
.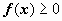 непрерывна на отрезке [ a, b ], то существует точка
непрерывна на отрезке [ a, b ], то существует точка  В этом разделе переменную интегрирования будем обозначать буквой t, а буквой x обозначим верхний предел интегрирования. Будем считать, что верхний предел интеграла может меняться, т.е. что x - переменная, в результате интеграл будет функцией Ф(x) своего верхнего предела:
В этом разделе переменную интегрирования будем обозначать буквой t, а буквой x обозначим верхний предел интегрирования. Будем считать, что верхний предел интеграла может меняться, т.е. что x - переменная, в результате интеграл будет функцией Ф(x) своего верхнего предела:  . Легко доказать, что если f (t) интегрируема, то Ф(x) непрерывна, но для нас важнее следующая фундаментальная теорема:
. Легко доказать, что если f (t) интегрируема, то Ф(x) непрерывна, но для нас важнее следующая фундаментальная теорема: .
. 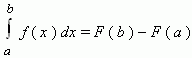
 [α,β].
[α,β].
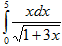
 . Тогда
. Тогда  и
и  . Если х=0, то t=1 и, если х=5, то t=4. Выполняя замену, получим:
. Если х=0, то t=1 и, если х=5, то t=4. Выполняя замену, получим:
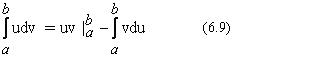


 ,
2)
,
2) 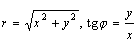 .
.









