
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 10. Криволинейный интеграл.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пискунов, гл. XV, § 1-2, упр. 1-5 Данко, гл. II, § 1-4
Криволинейные интегралы по длине дуги и по координатам. Основные формулы.
1. Определение криволинейного интеграла по длине дуги (1-го рода).
где h=AB, имеющая уравнение y= j(x) dh-дифференциал дуги ABили h.
2.Вычисление криволинейного интеграла по длине дуги (1-го рода).
где j/(x)- производная y.
3.Определение криволинейного интеграла по координатам (2-го рода).
Криволинейный интеграл по координатам (II-го рода) есть работа, совершаемая переменной силой
4.
5.
(A C B)
6.Криволинейный интеграл II-го рода (по координатам) вычисляется по формуле:
где 7.
т.е криволинейный интеграл по любому замкнутому контуру равен нулю.
8.
Этот факт используется в качестве наивыгоднейшего пути интегрирования (следует выбрать ломаную, соединяющую точки А и В, звенья которой параллельны осям (OX) и (OY).
Подынтегральное выражение
9. Площадь фигуры, ограниченной простым замкнутым контуром С, находится по формуле: 10.2. Примеры решения задач.
Задача 1. Вычислить криволинейный интеграл I-го рода по длине дуги
Решение:
Уравнение прямой имеет вид:
Находим
Задача 2. Вычислить площадь фигуры, ограниченной кривыми y= x2, x= y2и 8xy=1.
Решение:
Решая совместно уравнения кривых находим координаты точек A и B:
Значит,
Это краткое решение. Более подробное решение имеет вид:
1. 2.
3.
Задача 3. Дано Проверить, что данное выражение является полным дифференциалом функции «U» и найти эту функцию.
Решение:
выражение можно записать
Будем интегрировать dUпо ломаной OAM(см. рис.)
O(0;0) A(x;0) x
Учтя, что на пути [OA] y=0; dy=0 а на пути [AM] x=const, dx=0, получим:
Ответ:
Задача 4. Найти центр тяжести дуги полуокружности
Решение: Из соображения симметрии ясно, что центр тяжести лежит на оси (OY), поэтому Xc=0.
Тогда
Ответ:
Вопросы для самопроверки.
Контрольная работа № 2 В ЗАДАЧАХ 91-100 найти неопределённые интегралы способом подстановки (методом замены переменной).
91.
93.
95.
97.
99.
В ЗАДАЧАХ 101-110 найти неопределённые интегралы применяя метод интегрирования по частям.
101.
103.
105.
107.
109.
В ЗАДАЧАХ 111-120 найти неопределённые интегралы, пользуясь разложением рациональных дробей на простейшие.
111.
113.
115.
117.
119.
В ЗАДАЧАХ 121-130 вычислить определённые интегралы.
121.
123.
125.
127.
129.
В ЗАДАЧАХ 131-140 вычислить площадь, ограниченную заданными параболами. 131.
132.
133.
134.
135.
136.
137.
138.
139.
140.
В ЗАДАЧАХ 141-150 найти длину дуги кривой.
141.
143.
145.
147.
149.
В ЗАДАЧАХ 151-160 вычислить несобственные интегралы и установить их расходимость.
151.
153.
155.
157.
159.
В ЗАДАЧАХ 161-210 вычислить частные производные первого и второго порядков от заданных функций.
161.
163.
165.
167.
169.
В ЗАДАЧАХ 171-180 задана функция z= f(x,y). Найти градиент и производную этой функции в заданной точке M(x0, y0) в направлении вектора 171.
172.
173.
174.
175.
176. z =ln (x2+y2), M (3,4),
177.
178.
179.
180.
В ЗАДАЧАХ 181-190 найти экстремум заданной функции.
181.
183.
185.
187.
189.
В ЗАДАЧАХ 191-200 с помощью двойного интеграла вычислить координаты центра тяжести фигуры, ограниченной заданными линиями (поверхностную плотность считать равной единице).
191.
193.
195.
197.
199.
В ЗАДАЧАХ 201-210 вычислить работу, совершаемую переменной силой
201. 202. 203. N(2;8).
204. N(2;32)
205. M(1;2) и N (3;5) 206. N (3;30).
207. M(0;1), N(1;2).
208. M(1;3), N(2;10).
209.
210. N (3;29).
|
||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 515; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.223.30 (0.007 с.) |




 имеющая уравнение y=j(x),
имеющая уравнение y=j(x),

 на криволинейном пути AB(механическое толкование).
на криволинейном пути AB(механическое толкование).




 не зависит от контура интегрирования между т. А и т. В, если выполняется тождественное равенство:
не зависит от контура интегрирования между т. А и т. В, если выполняется тождественное равенство: 
 при указанных условиях
при указанных условиях  является полным дифференциалом некоторой однозначной функции
является полным дифференциалом некоторой однозначной функции  т.е
т.е  а уравнение
а уравнение  называется дифференциальным уравнением в полных дифференциалах.
называется дифференциальным уравнением в полных дифференциалах.
 где L- отрезок прямой от т. O(0;0) до B(4;3)
где L- отрезок прямой от т. O(0;0) до B(4;3) или
или 
 тогда
тогда 

 Þ
Þ 
 Þ
Þ 
 или
или 

 или
или 
 -дуга параболы y= x2; dy=2xdx; тогда
-дуга параболы y= x2; dy=2xdx; тогда 
 - дуга кривой
- дуга кривой  тогда
тогда 

 -дуга кривой
-дуга кривой 
 тогда
тогда



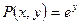



 - требование полного дифференциала выполняется и данное
- требование полного дифференциала выполняется и данное , где U=U(x,y)- искомая функция.
, где U=U(x,y)- искомая функция. y. M (x;y)
y. M (x;y)


 лежащей в верхней полуплоскости. Плотность считать равной единице.
лежащей в верхней полуплоскости. Плотность считать равной единице. Ордината
Ордината  , где dL-длина дуги.
, где dL-длина дуги.

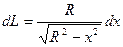

 - длина полуокружности, т.е
- длина полуокружности, т.е 


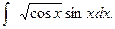 . 92.
. 92. 
 94.
94. 
 96.
96. 
 98.
98. 
 100.
100. 
 102.
102. 
 104.
104. 
 106.
106. 
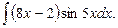 108.
108. 
 110.
110. 
 112.
112. 
 114.
114. 
 116.
116. 
 118.
118. 
 120.
120. 
 122.
122. 
 124.
124. 
 126.
126. 
 128.
128. 
 130.
130. 




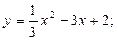
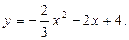















 142.
142. 


 144.
144. 






 150.
150. 

 152.
152. 
 154.
154. 
 156.
156. 
 158.
158. 
 160.
160. 
 162.
162. 
 164.
164. 
 166.
166. 
 168.
168. 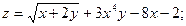
 170.
170. 
 составляющего угол a с положительным направлением оси OX.
составляющего угол a с положительным направлением оси OX.




 M (2,2),
M (2,2), 




 M (1,-2),
M (1,-2), 
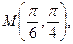
 M (1,1),
M (1,1),  M (2,2),
M (2,2),  182.
182. 
 184.
184. 
 186.
186. 
 188.
188. 
 190.
190. 
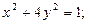 -x+2y = 1 192.
-x+2y = 1 192. 

 3x - 4y =1 194. x2+y2 =9;
3x - 4y =1 194. x2+y2 =9; 

 196.
196.  x-5y =1.
x-5y =1. x-3y-3 =0. 198.
x-3y-3 =0. 198.  2x-5y-1 =0.
2x-5y-1 =0.
 200.
200.  x+y+2=0.
x+y+2=0. на криволинейном пути L, соединяющем заданные точки M и N.
на криволинейном пути L, соединяющем заданные точки M и N. L -дуга параболы y=x2+2x;M(0;0),N(1;3)
L -дуга параболы y=x2+2x;M(0;0),N(1;3) L - дуга параболы y=2x2+1;M(0;1), N(2;9)
L - дуга параболы y=2x2+1;M(0;1), N(2;9) L -дуга кубической параболы y=x3; M(0;0),
L -дуга кубической параболы y=x3; M(0;0), L - дуга параболы y=7x2+2x; M(0;0),
L - дуга параболы y=7x2+2x; M(0;0), L - отрезок прямой, соединяющий точки
L - отрезок прямой, соединяющий точки L - дуга параболы y=3x2+x; M(1;4),
L - дуга параболы y=3x2+x; M(1;4), L - дуга кубической параболы y=x3+1;
L - дуга кубической параболы y=x3+1; L -дуга кубической параболы y=x3+2;
L -дуга кубической параболы y=x3+2; L - дуга параболы y=x2+x; M(1;2), N(3;12).
L - дуга параболы y=x2+x; M(1;2), N(3;12). L - дуга параболы y=3x2+2; M(2;14),
L - дуга параболы y=3x2+2; M(2;14),



