
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 7. Неопределённый интеграл.Содержание книги
Поиск на нашем сайте
Пискунов, гл X, § 1-14, упр. 1-214. Данко, гл IX, § 1-5.
7.1 Определение неопределённого интеграла. Непосредственное интегрирование. Определение 1. Функция F (x) называется первообразной для функции f (x), если F´ (x)=f (x) и dF (x)= f (x)dx. Если функция f (x) имеет первообразную F (x), то она имеет бесчисленное множество первообразных вида F (x)+С, где C- постоянная.
Определение 2. Неопределённым интегралом от функции f (x) или от выражения f (x)dx называется совокупность всех её первообразных. Обозначение: Знак f (x)- подынтегральная функция f (x)dx- подынтегральное выражение x- переменная величина (аргумент функции) F (x)- первообразная F(x)+С –совокупность первообразных. Отыскание неопределённого интеграла называется интегрированием функции.
Таблица неопределённых интегралов.
1.
2.
3.
4.
6.
8.
9.
10.
11.
13.
15.
Свойства дифференциалов. 1. 2.
Под непосредственным интегрированием понимается сведение подынтегрального выражения к табличному виду путём использования тождественных преобразований, таблицы и свойств неопределённых интегралов и дифференциалов.
Например: Найти Решение: Возведём двучлен во вторую степень и запишем каждое слагаемое в виде степени, затем, произведя почленное деление и, применив соответствующие формулы таблицы, получим:
7.2 Способы интегрирования.
Классы функций, интегрируемых по частям:
б).
3. Разложение правильной рациональной дроби на простейшие:
Для частных случаев:
а) формулы понижения порядка:
б) Формулы преобразования произведения тригонометрических функций в сумму:
5. Интегралы вида
В частности:
для
для
6. Интегрирование иррациональностей.
а)
б)
в) Тригонометрические подстановки:
Например: 1)
2) 3) Примеры 1-3 решить самостоятельно.
Примеры решения задач.
№1 Найти Решение. Данный интеграл не является табличным. Умножив на
d3x
№ 2. Найти интеграл:
Решение. Используем интегрирование по частям, т.е используем формулу:
Имеем:
№ 3. Найти интеграл:
Решение: Используем подстановку, чтобы сделать подынтегральное выражение рациональным (без корня). Итак,
Тогда Jпримет вид:
Использованы операции:
1. Замена 2.Вынесен постоянный множитель 2. 3.Умножим и разделим на (-1). 4.В числителе подынтегральной дроби прибавили (+1) и (-1). 5.Использовано свойство:
6.Применили табличные формулы:

7.3 Вопросы для самопроверки. 1. Дайте определение первообразной функции неопределённого интеграла. Приведите примеры. 2. Сформулировать свойства неопределённого интеграла. 3. В чём заключается геометрический смысл неопределённого интеграла? 4. Назовите основные методы интегрирования.
5. Решите: 6. Примените формулу интегрирования по частям к интегралу:
7. Объяснить, почему ∫x2cosx3dx решается способом подведения функции под знак дифференциала. Можно ли решить этот интеграл методом подстановки?
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 354; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.46.108 (0.006 с.) |


 - знак интеграла
- знак интеграла

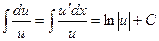

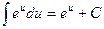
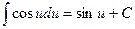 5.
5. 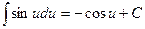
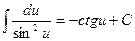 7.
7. 






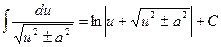 12.
12. 
 14.
14. 
 .
. , с- const
, с- const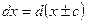 Например:
Например: 





 a).
a). 





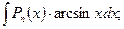



 в).
в). 
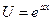
 или
или  или U= cosbx
или U= cosbx
 4. Интегралы вида
4. Интегралы вида -универсальная подстановка;
-универсальная подстановка; 




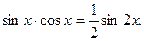



 и
и 
 Подстановка
Подстановка 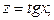


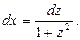
 применяется формула
применяется формула 
 -формула
-формула 
 подстановка
подстановка 
 подстановка
подстановка 






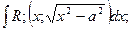

 решается способом интегрирования по частям.
решается способом интегрирования по частям.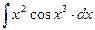 решается способом подведения функции под знак дифференциала.
решается способом подведения функции под знак дифференциала. - решается методом подстановки x=sint.
- решается методом подстановки x=sint.
 и на (3) одновременно подинтегральное выражение, получим:
и на (3) одновременно подинтегральное выражение, получим:
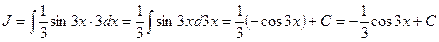


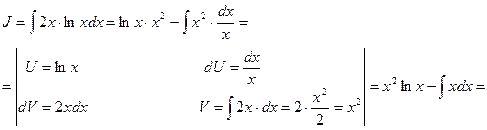

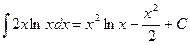




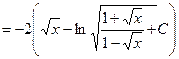
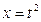

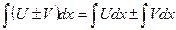


 .
.
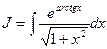 методом подстановки.
методом подстановки.



