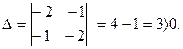Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 9. Функции нескольких переменных.Содержание книги
Поиск на нашем сайте
Пискунов, гл VIII, § 1-17, гл IX, § 6. упр 1-49. Данко, гл VIII, § 1-4.
9.1 Определение функции 2-х аргументов. Область определения функции.
Определение. Если каждой паре действительных чисел (x,y) Î D по некоторому правилу (закону) поставлено в соответствие одно и только одно значение переменной ZÎ E, то говорят, что на множестве D задана функция z =f(x,y). Множество D-область определения функции. Область D есть часть плоскости, ограниченная замкнутой линией. Графиком функции z =f(x,y) является некоторая поверхность Q.
Задача. Найти область определения функции
Решение: Функция zпринимает действительные значения при условии a2-x2-y2≥0→x2+y2≤ a2 круг с центром в начале координат, радиус круга a.
Ответ: Областью определения данной функции является круг вида x2+y2 ≤ a2 (граница-окружность включается) Изображение области определения на координатной плоскости ХОУ.
9.2 Производные и дифференциалы функции 2-х аргументов.
Основные формулы.
1.
2.
При вычислении полный дифференциал функции
где
4.
а), где - полное приращение функции.
Эта функция используется в нахождении приближённых значений функции.
6.
8. Если z=f(x,y), где
вычисляется по формуле:
9.3 Примеры решения задач. Задача 1.
Решение:
Задача 2. Найти полный дифференциал функции z= x3y+ xtgx
Решение: - теоретическая формула.
Где
Задача 3. Вычислить приближённое значение функции в точке P(2,97;4,02)
Решение:
т.Р
Тогда
Или
Или
Задача 4. Найти производную функции в направлении, составляющим с положительным направлением оси (ОХ) угол a=60°.
Решение:
 , где aи b- углы наклона вектора , где aи b- углы наклона вектора  к оси и к оси (OY)+ соответственно. к оси и к оси (OY)+ соответственно.
a=60°, тогда b=30°
 
Задача 5. Вычислить градиент функции
Решение:
Задача 6. Найти смешанные частные производные второго порядка функции
Решение:
Дифференцируя, Дифференцируя
Ответ:
Задача 7. Исследовать на экстремум функцию
Решение: (1)
(2)
Неравенство (2) является достаточным условием экстремума.
Причём, если И если
Имеем:
 
то в точке P0(0;3) есть максимум
Ответ:
Задача 8.
Найти наибольшее и наименьшее значения функции
Решение. Чтобы найти наибольшее, и наименьшее значения функции в заданной замкнутой области, необходимо:
1) найти стационарные точки, лежащие внутри области, и вычислить значения функции в этих точках; исследовать на экстремум эти точки не следует; 2) найти наибольшее и наименьшее значения функции на границе области; если граница состоит из нескольких линий, то исследование проводится для каждого участка в отдельности; 3) сравнить полученные значения функции и установить наибольшее и наименьшее значения функции в заданной замкнутой области.
Находим стационарные точки, лежащие внутри заданной области:
Приравняв нулю частные производные и решив полученную систему
находим стационарную точку Р0(1; 2). Эта точка принадлежит заданной области. Вычислим значение функции в этой точке:
Граница области состоит из отрезка ОА оси Ох, отрезка 0В оси Оу и отрезка АВ. Определим наибольшее и наименьшее значения функции z на каждом из этих трех участков. На отрезке ОА у = 0, а 0 £ x £ 4. Если у=0, то z(x) = х2 — 2x + 5. Находим наибольшее и наименьшее значения этой функции на отрезке [0, 4]:
Вычислим значения функции на концах отрезка ОА, т. е. в точках 0(0; 0) и A(4; 0):
z(0) = 5, z(4)= 13.
На отрезке OB х = 0 и 0 £ y £ 4. Если х = 0, то z(y) = 2у 2 -8у + 5. Находим наибольшее и наименьшее значения функции z от переменной у на отрезке [0; 4]:
В точке О (0; 0) значение функции уже было найдено. Вычислим значение функции в точке В:
z(В) = z (0; 4) = 5.
Теперь исследуем отрезок АВ. Уравнением прямой АВ будет у = 4 - х. Подставив это выражение- для у в заданную функцию z, получим
Определим наибольшее и наименьшее значения этой функции на отрезке [0; 4]:
Рз — стационарная точка на отрезке АВ. Вычислим значение функции в этой точке:
Значения функции на концах отрезка АВ найдены ранее.
Сравнивая полученные значения функции z в стационарной точке Ро заданной области, в стационарных точках на границах области P1, Р2, Рз и в точках О, А и В, заключаем, что наибольшее значение в заданной замкнутой области функция z имеет в точке А, наименьшее значение — в точке Ро(1; 2). Итак,
Задача 9. Найти
Решение:
Речь идёт о дифференцировании сложной функции.
Используя формулу
Задача 10.
Исследовать на экстремум функцию z = - 4 + 6x- х2 – ху- у2. Решение: Чтобы исследовать данную дважды дифференцируемую функцию z = f (x, у) на экстремум, необходимо: 1. Найти частные производные первого порядка
Каждая пара действительных корней этой системы определяет одну стационарную точку исследуемой функции. Пусть ро (х0 , у0) одна из этих точек. 2. Найти частные производные второго порядка
Положим, что
3. Составить и вычислить определитель второго порядка
4. Если в исследуемой стационарной точке р0(x0, y0) D>0, то функция z = f(x, у) в этой точке имеет максимум при A<0 и минимум при A>0; если D<0, то в исследуемой точке нет экстремума. Если D = 0, то вопрос об экстремуме требует дополнительного исследования.
Находим стационарные точки заданной функции:
Решение системы
Следовательно, данная функция имеет только одну стационарную точку Ро(4, - 2). Находим частные производные второго порядка и их значения в найденной стационарной точке:
Как видно, частные производные второго порядка не содержат х, они постоянны в любой точке и, в частности, в точке Р0(4, -2). Имеем А = -2; В = - 1; С=- 2.
Так как D>0 и A<0, то в точке Ро(4; -2) данная функция имеет максимум:
9.10 Вопросы для самопроверки. 1. Сформулируйте определения функции двух, трёх переменных. Каков геометрический смысл функции двух независимых переменных?
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 269; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.140.108 (0.009 с.) |




 - частная производная 1-го порядка функции z по переменной x.
- частная производная 1-го порядка функции z по переменной x. - частная производная 1-го порядка функции Z по переменной y.
- частная производная 1-го порядка функции Z по переменной y. вычисляется при постоянном y,
вычисляется при постоянном y,  вычисляется при постоянном x.
вычисляется при постоянном x.

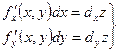 - частные дифференциалы
- частные дифференциалы функции
функции Для дифференцируемой функции справедливы приближённые равенства.
Для дифференцируемой функции справедливы приближённые равенства.

 , dz- полный дифференциал.
, dz- полный дифференциал.
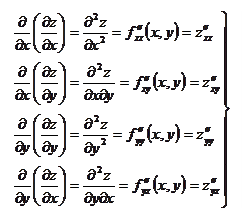 5.Частными производными второго порядка от функции
5.Частными производными второго порядка от функции  называются частные производные от её частных производных первого
называются частные производные от её частных производных первого порядка.
порядка. - дифференциал второго порядка для функции
- дифференциал второго порядка для функции 
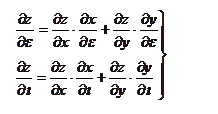
 7. Если z= f(x,y), где x= φ(t), y=ψ(t), то
7. Если z= f(x,y), где x= φ(t), y=ψ(t), то  - производная сложной функции. z=f(φ(t),ψ(t)).
- производная сложной функции. z=f(φ(t),ψ(t)). то
то
 9. Производная неявной функции, заданной уравнением,где F(x,y)-дифференцируемая функция,
9. Производная неявной функции, заданной уравнением,где F(x,y)-дифференцируемая функция,

 10. Частные производные неявной функции заданной уравнением вычисляются по формулам:
10. Частные производные неявной функции заданной уравнением вычисляются по формулам:
 при условии
при условии 

 Найти
Найти  .
.
 , где
, где 

















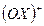


 - ответ.
- ответ. в точке А (2;1).
в точке А (2;1). , где
, где 
 - базисные векторы, орты.
- базисные векторы, орты.







 получаем
получаем 
 по x(y=const), получаем
по x(y=const), получаем 


 - необходимое условие экстремума.
- необходимое условие экстремума. где
где  является решением системы (1).
является решением системы (1). то в точке
то в точке  есть максимум функции.
есть максимум функции. то в точке
то в точке 

 (1)
(1)  Þ
Þ 




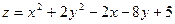 в замкнутом треугольнике АОВ, ограниченном осями координат и прямой x + y -4=0 (рис. 12).
в замкнутом треугольнике АОВ, ограниченном осями координат и прямой x + y -4=0 (рис. 12).





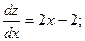






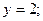








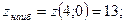

 если
если  , где x=acost, y=asint.
, где x=acost, y=asint. получим
получим 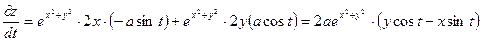

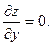


 и вычислить их значения в каждой стационарной точке.
и вычислить их значения в каждой стационарной точке.





 даёт x0= 4, y0= -2.
даёт x0= 4, y0= -2.