
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные правила дифференцированияСодержание книги
Поиск на нашем сайте
Пусть С- постоянное, Тогда: 1) 2) 3) 4) 5) 6) 7) если
Примеры решения задач Задача 1. Найти производные а) б) в) г)
Решение: а) Пользуясь правилом логарифмирования корня и дроби, преобразуем правую часть:
Применяя правила и формулы дифференцирования, получим:
б) Предварительно прологарифмируем по основанию е обе части равенства:
Теперь дифференцируем обе части, считая
откуда
в) В данном случае зависимость между аргументом х и функцией у задана уравнением, которое не разрешено относительно функции у. Чтобы найти производную у', следует дифференцировать по х обе части заданного уравнения, считая при этом у функцией от х, а затем полученное уравнение решить относительно искомой производной у'. Имеем
Из полученного равенства, связывающего х, у, и у', находим производную у':
откуда
г) Зависимость между переменными х и у задана параметрическими уравнениями. Чтобы найти искомую производную у', находим предварительно дифференциалы dy и dx и затем берем отношение этих дифференциалов
Задача 2. Найти производную второго порядка а) б) Решение: а) Функция у задана в неявном виде. Дифференцируем по х обе части заданного уравнения, считая при этом у функцией от х:

откуда
Снова дифференцируем по х обе части (1):
Заменив у' в (2) правой частью (1), получим:
б) Зависимость между переменными xи у задана параметрическими уравнениями. Чтобы найти производную у', находим сперва дифференциалы dy и dx и затем берем отношение этих дифференциалов:
Тогда
Производная второго порядка Тогда
Задача 3. Найти приближенное значение функции Решение: Известно, что дифференциал dy функции
Пусть
Тогда

Приближенное равенство (1) дает возможность найти значение функции при
Применяя (1), получаем
Вопросы для самопроверки 1. Сформулировать определение производной. 2. Каков геометрический смысл производной? 3. Как составить уравнение касательной? 4. Каков геометрический и механический смысл производной? 5. Как найти производную неявной функции? Параметрической функции? 6. Функция непрерывна в т. x0. Следует ли отсюда дифференцируемость функции? 7. В чём заключается геометрический смысл дифференциала функции? 8. Записать формулу, используемую в приближённых вычислениях. Найти приближённое значение
|
||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 245; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.198.250 (0.006 с.) |

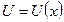 и
и  - функции имеющие производные.
- функции имеющие производные.





 ,
,  , где функции f(U) и U(x) имеют производные, то
, где функции f(U) и U(x) имеют производные, то  - правило дифференцирования сложной функции.
- правило дифференцирования сложной функции. или
или  следующих функций:
следующих функций:






 сложной функцией от переменной х:
сложной функцией от переменной х:


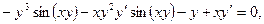










 (2)
(2)



 . Следовательно, чтобы найти у", надо найти дифференциал dy':
. Следовательно, чтобы найти у", надо найти дифференциал dy': 

 при
при  исходя из ее точного значения при
исходя из ее точного значения при 
 представляет собой главную часть приращения этой функции
представляет собой главную часть приращения этой функции  .Если приращение аргумента
.Если приращение аргумента  мало по абсолютной величине, то приращение
мало по абсолютной величине, то приращение  . Так как
. Так как  , а
, а  то имеет место приближенное равенство:
то имеет место приближенное равенство:
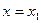 ,
, 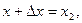 т. е.
т. е. 

 , если известно значение функции и ее производной при
, если известно значение функции и ее производной при  Прежде чем воспользоваться приближенным равенством (1), находим числовое значение производной f'(x) при х= 6:
Прежде чем воспользоваться приближенным равенством (1), находим числовое значение производной f'(x) при х= 6:
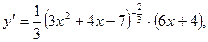 или
или 






