
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 8. Определённыйинтеграл по отрезку.Содержание книги
Поиск на нашем сайте
Определение: Определённым интегралом по отрезку [a;b]от функции f(x) называется предел интегральной суммы
Числа a,bназываются соответственно нижним и верхним пределами интегрирования, т.е [a;b]-отрезок интегрирования.
Свойства определённого интеграла по [a;b].
1.
2.
3.
4.
5.
Правила вычисления определённого интеграла по [a;b]
2.
3.
Например: Найти значение определённого интеграла
Решение:
Решаем методом подстановки
Положим
Тогда
8.1 Несобственные интегралы. К несобственным интегралам относятся:
Пример 1.
Пример 2. Вычислить
Решение
Пример 3. Вычислить
Решение: Т.к
Тогда Замечание. Если предел несобственного интеграла существует и конечен, то несобственный интеграл называется сходящимся.
Если же предел не существует или равен бесконечности, то интеграл называется расходящимся.
8.2 Приложения определённого интеграла по [a;b]
1.
2. параметрически: 3.
5. Вычисления объёма тела вращения.
6. Статические моменты и моменты инерции дуги плоской кривой y=f(x), (a £ x £ b) вычисляются по формулам (соответственно):
где
7. Координаты центра тяжести однородной дуги плоской кривой y=f(x) (a £ x £ b) выражаются формулами:
Примеры решения задач. Задача 1. Найти площадь фигуры, ограниченной параболой y=4x-x2 и осью ОХ.
Решение:
Решая систему, найдём точки пересечения: x=0; x=4. Фигура OABO- криволинейная трапеция.
Значит,
Задача 2. Найти длину дуги кривой y2=x3 от x=0 до x=1, (y ³ 0).
Решение: Дифференцируем уравнение кривой Имеем:
Задача 3. Найти статический момент и момент инерции полуокружности (-r £ x £ r) относительно оси OX.
Решение. 1.
2. Введём подстановку
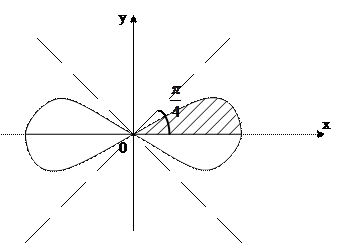
Следовательно Задача 4. Найти площадь, заключённую внутри лемнискаты Бернулли
Решение: В силу симметрии достаточно вычислить одну четверть искомой площади, а затем учетверить результат.
По формуле
Отсюда S=a2
8.3 Вопросы для самопроверки.
4. По какой формуле вычисляется
5. Дайте определение несобственного интеграла.
6. Является ли 7. Геометрический смысл несобственных интегралов.
8. В каких задачах используются определённые интегралы по отрезку [a;b] в геометрии? В механике?
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 250; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.105.122 (0.005 с.) |

 , если этот предел существует и не зависит ни от деления отрезка [a;b]на части, ни от выбора точек t внутри каждой из частей при условии, что длина наибольшего из частичных отрезков (∆xi) стремится к нулю, т.е
, если этот предел существует и не зависит ни от деления отрезка [a;b]на части, ни от выбора точек t внутри каждой из частей при условии, что длина наибольшего из частичных отрезков (∆xi) стремится к нулю, т.е




 С- постоянная
С- постоянная 1.
1.  - формула Ньютона-Лейбница, где F(x)- первообразная
- формула Ньютона-Лейбница, где F(x)- первообразная
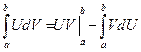 - интегрирование по частям.
- интегрирование по частям.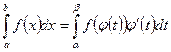 , где x=j(t) функция непрерывная вместе со своей производной
, где x=j(t) функция непрерывная вместе со своей производной на [a;b]
на [a;b] 







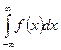
 - несобственный интеграл 2) типа, т.к на отрезке [-2;9]функция
- несобственный интеграл 2) типа, т.к на отрезке [-2;9]функция  терпит бесконечный разрыв в точке x=0.
терпит бесконечный разрыв в точке x=0.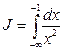



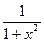 - чётная функция.
- чётная функция.
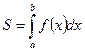 -площадь криволинейной трапеции, где y=f(x)- кривая, ограничивающая криволинейную трапецию, aABb- криволинейная трапеция.
-площадь криволинейной трапеции, где y=f(x)- кривая, ограничивающая криволинейную трапецию, aABb- криволинейная трапеция.
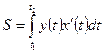 - площадь криволинейной трапеции, если кривая задана
- площадь криволинейной трапеции, если кривая задана
 - площадь криволинейного сектора, ограниченного кривой, заданной в полярных координатах, где r= r(a) - уравнение кривой.
- площадь криволинейного сектора, ограниченного кривой, заданной в полярных координатах, где r= r(a) - уравнение кривой.
 Если криволинейная трапеция вращается вокруг оси OX, то объём тела вращения вычисляется по формуле:
Если криволинейная трапеция вращается вокруг оси OX, то объём тела вращения вычисляется по формуле: 

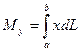


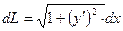 - дифференциал дуги кривой y=f(x)
- дифференциал дуги кривой y=f(x)
 где
где  L-длина дуги.
L-длина дуги.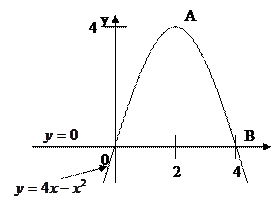

 (кв. ед)
(кв. ед)
 (ед.)
(ед.)




 .
.  Если x=0, то t=0, если x=r, то
Если x=0, то t=0, если x=r, то  .
.

 имеем
имеем

 несобственными?
несобственными?


