
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Редакционно-издательским Советом ТГСХА в качествеСодержание книги
Поиск на нашем сайте
ВЫСШАЯ МАТЕМАТИКА Программа, методические указания и задания для контрольных работ № 1,2 для студентов-заочников первого курса инженерных специальностей ТГСХА. Часть I
Тюмень, 2008 Утверждено Редакционно-издательским Советом ТГСХА в качестве методических указаний
Программа, методические указания и задания для выполнения контрольных работы для студентов заочной формы обучения составлены в соответствии с рабочей программой учебной дисциплины «Математика»
Составители: доцент кафедры математики Дьячкова Л.И. старший преподаватель кафедры математики Пинаева Г.М. старший преподаватель кафедры математики Антропов В.А.
Научный редактор Столярова О.А., ст. преподаватель
Обсуждено на заседании кафедры математики Протокол № 2 от «15» ноября 2004 г.
Одобрено научно-методическим советом института экономики и финансов. Протокол № 7 от «19» марта 2004 г. Содержание:
Программа курса высшей математики…………………………………стр.4
Методика самостоятельной работы студента………………………….стр.8
Таблица вариантов контрольных работ………………………………..стр.9
Указания к выполнению контрольной работы № 1………………….стр.10
Контрольная работа №1………………………………………………..стр.38
Указания к выполнению контрольной работы № 2…………………..стр.44
Контрольная работа № 2……………………………………………..…стр.72
Рабочая программа курса. «Высшая математика» для инженерно-технических специальностей.
Содержание программы.
I. Элементы линейной алгебры и аналитической геометрии.
1. Трехмерное пространство R3. Векторы. Линейные операции над векторами. Линейно-независимые системы векторов. Базис. 2. Скалярное произведение в R3 и его свойства. Длина вектора. Угол между двумя векторами. Ортогональный базис. Разложение вектора по базису. 3. Определители второго и третьего порядков, их свойства. Алгебраические дополнения и миноры. Определители n-го порядка. Векторное произведение и его свойства. Смешанное произведение. 4. Уравнение плоскости в R3 (векторная и координатная формы). Уравнения прямой в R2 и R3 (векторная и координатная формы). 5. Системы двух и трех линейных уравнений с двумя и тремя неизвестными. Правило Крамера. Системы т линейных уравнений с п неизвестными. Метод Гаусса-Жордана.
6. Матрицы. Действия над матрицами, обратная матрица. Матричная запись системы линейных уравнений и ее решения. Пространство Rn. Линейная зависимость и независимость векторов в Rn. Ранг матрицы, его вычисление. Исследование системы линейных уравнений. Теорема Кронекера-Капелли. 7. Понятие о линейном операторе как о линейном преобразовании пространства. Линейные операторы и их матрицы в R 2 и R3. Собственные векторы и собственные значения линейных операторов. 8. Квадратичные формы. Приведенные к каноническому виду. Геометрические приложения квадратичных форм в пространствах R2 и R3. 9. Общее уравнение кривых второго порядка. Канонические формы уравнений эллипса, гиперболы и параболы. Геометрические свойства эллипса, гиперболы и параболы. 10. Поверхности второго порядка, Канонические формы уравнений. Исследование поверхностей второго порядка методом сечений.
IV. Исследование функций с помощью производных
27. Условия возрастания и убывания функции. Точки экстремума. Необходимые условия экстремума. Достаточные признаки существования экстремума. Отыскание наибольшего и наименьшего значений непрерывной на отрезке функции. 28. Исследование функции на экстремум с помощью производных высшего порядка. Исследование функций на выпуклость и вогнутость. Точки перегиба. Асимптоты кривых. Общая схема построения графиков функций.
V. Неопределенный интеграл.
29. Первообразная. Неопределенный интеграл, его свойства. Таблица основных формул интегрирования. Непосредственное интегрирование по частям и подстановкой. 30. Интегрирование рациональных функций путем разложения на простейшие дроби. Интегрирование выражений, содержащих тригонометрические функции. Интегрирование некоторых иррациональных выражений. Использование таблиц интегралов. VI. Определенный интеграл.
31. Задачи, приводящие к понятию определенных интегралов. Определенный интеграл как предел интегральных сумм. Основные свойcтва определенного интеграла. 32. Производная интеграла по верхнему пределу. Формула Ньютона — Лейбница.
33. Вычисление определенного интеграла: интегрирование по частям и подстановкой. Приближенное вычисление определенного интеграла: формулы прямоугольников, трапеций и Симпсона. 34. Приложение интегралов к вычислению площадей плоских фигур, длин дуг кривых, объемов тел и площадей поверхностей вращения. Физические приложения определенного интеграла. 35. Несобственные интегралы с бесконечными пределами. Несобственные интегралы от неограниченных функций, основные свойства. Абсолютная и условная сходимости. Признаки сходимости.
VIII. Кратные интегралы. 42. Задачи, приводящие к понятию кратного интеграла. Двойные и тройные интегралы, их основные свойства. Представление об интегралах любой кратности. 43. Вычисление двойных и тройных интегралов в декартовых координатах. 44. Замена переменных в кратных интегралах. Переход от декартовых координат к полярным, цилиндрическим и сферическим координатам. 45. Применение кратных интегралов для вычисления объемов и площадей, для решения задач механики и физики.
Таблица заданий для контрольных работ №1 и №2.
Решение
(первую строку умножаем на (-2) и на (-3) и складываем последовательно со второй и третьей строкой соответственно) ~
(умножаем элементы второй строки на (-8) и складываем с 3-ей строкой). Имеем систему Из этой системы имеем z =0 (из последней строки), y= -3 (из 2-ой строки), x=2 (из 1-ой строки).
Вопросы для самопроверки
Понятие предела Определение. Число а называется пределом функции y =f(x) в т. Этот факт записывается так: Если Если Если
Если
Если
При вычислении пределов используются теоремы о пределах, а также 1-ый замечательный предел второй замечательный предел
4.2 Способы раскрытия неопределённостей вида
I. Если 1-ый способ. Разложить и числитель и знаменатель дроби на множители, затем сократить на общий множитель.
Пример
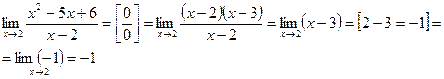
Ответ: где 2- предельное значение аргумента, (-1) -
предельное значение функции y.
2-ой способ. Использовать правило Лопиталя, т.е использовать равенство:
Пример: 3-ий способ. Применить таблицу эквивалентности бесконечно малых.
Таблица.
1.
2.
3.
4.
Пример: Найти
Решение.
1-ый способ. Использовать правило Лопиталя.
Пример. Найти
Решение: 2-ой способ. Разделить все слагаемые числителя и все слагаемые знаменателя на старшую переменную дроби. Пример. Найти Ответ:
Вопросы для самопроверки 1. Дайте определение функции, области определения. Приведите примеры. 2. Сформулируйте определение предела функции в точке. 3. Какая переменная величина называется бесконечно малой? Бесконечно большой в точке 4. Что означают выражения: 5. Приведите пример бесконечно малой функции в т. x=2 и бесконечно большой функции в этой же точке (аналитический и графический). 6. Каким свойством обладает приращение аргумента и приращение функции, если функция непрерывна в точке x0 ?
Таблица дифференциалов и производных основных элементарных функций
Примеры решения задач Задача 1. Найти производные а) б) в) г)
Решение: а) Пользуясь правилом логарифмирования корня и дроби, преобразуем правую часть:
Применяя правила и формулы дифференцирования, получим:
б) Предварительно прологарифмируем по основанию е обе части равенства:
Теперь дифференцируем обе части, считая
откуда
в) В данном случае зависимость между аргументом х и функцией у задана уравнением, которое не разрешено относительно функции у. Чтобы найти производную у', следует дифференцировать по х обе части заданного уравнения, считая при этом у функцией от х, а затем полученное уравнение решить относительно искомой производной у'. Имеем
Из полученного равенства, связывающего х, у, и у', находим производную у':
откуда
г) Зависимость между переменными х и у задана параметрическими уравнениями. Чтобы найти искомую производную у', находим предварительно дифференциалы dy и dx и затем берем отношение этих дифференциалов
Задача 2. Найти производную второго порядка а) б) Решение: а) Функция у задана в неявном виде. Дифференцируем по х обе части заданного уравнения, считая при этом у функцией от х:

откуда
Снова дифференцируем по х обе части (1):
Заменив у' в (2) правой частью (1), получим:
б) Зависимость между переменными xи у задана параметрическими уравнениями. Чтобы найти производную у', находим сперва дифференциалы dy и dx и затем берем отношение этих дифференциалов:
Тогда
Производная второго порядка Тогда
Задача 3. Найти приближенное значение функции Решение: Известно, что дифференциал dy функции
Пусть
Тогда

Приближенное равенство (1) дает возможность найти значение функции при
Применяя (1), получаем
Вопросы для самопроверки 1. Сформулировать определение производной. 2. Каков геометрический смысл производной? 3. Как составить уравнение касательной? 4. Каков геометрический и механический смысл производной? 5. Как найти производную неявной функции? Параметрической функции? 6. Функция непрерывна в т. x0. Следует ли отсюда дифференцируемость функции? 7. В чём заключается геометрический смысл дифференциала функции? 8. Записать формулу, используемую в приближённых вычислениях. Найти приближённое значение
План исследования функции и построения графика 1.Найти область определения функции. Решение этого вопроса указывает на те интервалы оси (ОХ), над которыми пройдёт график и на те значения аргумента x, над которыми график не пройдёт, а также в каких точках пройдут вертикальные асимптоты. 2.Исследовать на чётность, нечётность. Решение этого вопроса облегчает построение. 3.Указать промежутки монотонности функции и найти экстремумы её, точки экстремумов. Построить соответствующие точки на координатной плоскости. 4.Указать точки перегиба графика функции и нанести их на координатную плоскость. Указать промежутки выпуклости, вогнутости. 5.Найти уравнения вертикальных и наклонных асимптот, используя условия для существования этих асимптот. Построить эти линии на координатной плоскости.
6.Найти точки пересечения графика функции с осями координат. Нанести их на плоскость. 7.Исследовать поведение функции на концах области определения. Это поможет при построении графика. 8.Можно взять несколько контрольных точек, в случае уточнения поведения графика. 9.Построить график.
Задача 1. Исследовать функцию у = 1п(х2 — 6х +10) и построить ее график.
Решение: 1. Определим область существования функции. Квадратный трехчлен, стоящий под знаком логарифма, можно представить так: х2— 6x+10=(x-3)2 + 1. Как видно, под знаком логарифма будет положительное число при любом значении аргумента х. Следовательно, областью существования данной функции служит вся числовая ось. 2. Исследуем функцию на непрерывность. Функция всюду непрерывна и не имеет точек разрыва. 3. Установим четность и нечетность функции. Так как у(-х)¹у(х) и у(- х)¹ - у(х), то функция не является ни четной, ни нечетной. 4. Исследуем функцию на экстремум. Находим первую производную:
Знаменатель х2- 6x+10>0 для любого значения х. Как видно, при х < 3 первая производная отрицательна, а при х > 3 положительна. При х = 3 первая производная меняет свой знак с минуса на плюс. В этой точке функция имеет минимум:
Итак, A(3; 0) - точка минимума. Функция убывает на интервале (- ¥, 3) и возрастает на интервале (3, + ¥). 5. Определим точки перегиба графика функции и интервалы выпуклости и вогнутости кривой. Для этого находим вторую производную:
Разобьем всю числовую ось на три интервала: (- ¥, 2), (2, 4), (4, + ¥). Как видно, в первом и третьем интервалах вторая производная отрицательна, а во втором интервале положительна. При x1 = 2 и х2 = 4 вторая производная меняет свой знак. Эти значения аргумента являются абсциссами точек перегиба. Определим ординаты этих точек:
Следовательно, P1 (2; ln 2) и P2(4; ln 2) — точки перегиба графика функции. График является выпуклым в интервалах (- ¥, 2) и (4, +¥) и вогнутым в интервале (2, 4). 6. Определим уравнения асимптот графика функции. Для определения уравнения асимптоты y=kx+b воспользуемся формулами:
Имеем Чтобы найти искомый предел, дважды применяем правило Лопиталя:
Итак, кривая не имеет асимптот.
Вопросы для самопроверки. 1. Сформулируйте признаки возрастания (убывания) функции. Приведите примеры. 2. Дайте определение экстремума функции. 3. Как найти максимум, минимум функции (два правила)? 4. Приведите пример, когда обращение производной в нуль не является достаточным условием экстремума функции. 5. Как найти интервалы выпуклости (вогнутости) функции? Примеры. Контрольная работа № 1.
В ЗАДАЧАХ 1 –10 решить заданную систему уравнений, пользуясь формулами Крамера. Сделать проверку полученного решения.
1. 5x +8y-z= -7, 2. x+2y +z=4, x+2y+3z =1, 3x-5y+3z =1, 2x-3y +2z=9. 2x +7y- z=8.
3. 3x+2y + z= 5, 4. x+2y+4z=31, 2x+3y+ z =1, 5x+ y+ 2z=29, 2x + y+3z =11. 3x –y+ z=10.
5. 4x-3y +2z=9, 6. 2x-y- z =4, 2x+5y-3z=4, 3x+4y-2z=11, 5x+6y-2z=18. 3x-2y+4z =11.
7. x+ y+2z = -1, 8. 3x-y =5, 2x-y+2z= -4, -2x+ y+ z =0, 4x+ y+ 4z= -2. 2x- y+ 4z=15.
2x- 5y –3z= -17, 2x- y – 6z= -1, x + y- z= 0. 3x – 2y = 8.
В ЗАДАЧАХ 11-20 даны координаты вершин треугольника ABC. Найти: 1) длину стороны AB; 2) уравнения сторон AB и BC и их угловые коэффициенты; 3) внутренний угол B в радианах с точностью до 0,01; 4) уравнение медианы AE; 5) уравнение и длину высоты CD; 6) уравнение прямой, проходящей через точку E параллельно стороне AB.
11. A (1;-1), B (4;3), C (5;1). 12. A (0;-1), B(3,3), C(4;1). 13. A(1;-2) B (4;2), C (5;0). 14. A (2;-2), B (5;2), C (6;0). 15. A(0;0), B (3;4), C (4;2). 16. A (0;1), B (3;5), C (4;3). 17. A(3;-2), B (6;2), C (7;0). 18. A (3;-3), B (6;1), C (7;-1). 19. A (-1;1), B (2;5), C (3;3) 20. A (4;0), B(7;4), C (8;2).
В ЗАДАЧАХ 21-30 даны координаты вершин пирамиды ABCD. Требуется: 1. записать векторы 2. найти угол между векторами 3. найти проекцию вектора 4. найти площадь грани ABC; 5. найти объём пирамиды ABCD;
21. A (1;2;1), B (-1;5;1), C (-1;2;7), D (1;5;9). 22. A (2;3;2), B (0;6;2), C (0;3;8), D (2;6;10). 23. A (0;3;2), B (-2;6;2), C (-2;3;8), D (0;6;10). 24. A (2;1;2), B (0;4;2), C (0;1;8), D (2;4;10). 25. A (2;3;0), B (0;6;0), C (0;3;6), D (2;6;8). 26. A (2;2;1), B (0;5;1), C (0;2;7), D (2;5;9). 27. A (1;3;1), B (-1;6;1), C (-1;3;7), D (1;6;9). 28. A (1;2;2), B (-1;5;2), C (-1;2;8), D (1;5;10). 29. A (2;3;1), B (0;6;1), C (0;3;7), D (2;6;9). 30. A (2;2;2), B (0;5;2), C (0;2;8), D (2;5;10).
В ЗАДАЧАХ 31-40 найти указанные пределы.
31. 1)
2)
32. 1)
2)
33. 1)
2)
34. 1)
2)
35. 1)
2)
36. 1)
2)
37. 1)
2)
38. 1)
2)
39. 1)
2)
40. 1)
2)
В ЗАДАЧАХ 41-50 найти производные
41. а)
в)
42. а)
в)
43. а)
в)
44. а)
в)
45. а)
в)
46. а)
в)
47. а)
в)
48. а)
в)
49. а)
в)
50. а)
в)
В ЗАДАЧАХ 51-60 1). исследовать данные функции методами дифференциального исчисления и начертить их графики. 2). Для функции из пункта а) найти дополнительно наибольшее и наименьшее значения на отрезке [a;b]. 51. a)
б)
52. а)
б)
53. а)
б)
54. а)
б)
55. a)
б)
56. а)
б)
57. а)
б)
58. а)
б)
59. а)
б)
60. а)
б)
Решить ЗАДАЧИ 61-70 используя понятие экстремума функции.
61. Каковы должны быть размеры прямоугольника наибольшей площади, вписанного в круг радиуса 6 см? 62. Проволока длиной 40 см согнута в прямоугольник. Каковы должны быть размеры этого прямоугольника, чтобы площадь его была наибольшей? 63. Найти наибольший объем цилиндра, у которого полная поверхность равна S=24p (м2) 64. Найти наибольший объем конуса, образующая которого равна 64. Объем правильной треугольной призмы равен V= 16 (м3). Какова должна быть длина стороны основания призмы, чтобы ее полная поверхность была наименьшей? 65. Требуется изготовить ящик с крышкой, объем которого был бы равен 72 (см3), п
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 244; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.118.82 (0.016 с.) |




 ~
~ 


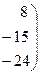 ~
~

 ~
~ 



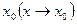 если для любого сколько угодно малого наперёд заданного ε>0 найдётся такое δ>0 (δ=δ(ε)), что выполняется неравенство
если для любого сколько угодно малого наперёд заданного ε>0 найдётся такое δ>0 (δ=δ(ε)), что выполняется неравенство  <e при
<e при  <
< 

 , то функцию
, то функцию  называют бесконечно большой величиной в окрестности т.
называют бесконечно большой величиной в окрестности т. 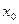 .
. , то
, то  - бесконечно малая функция (величина) в окрестности т. X0.
- бесконечно малая функция (величина) в окрестности т. X0.
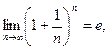
 , а также формулы
, а также формулы  ,
, 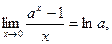

 и
и  .
. то можно использовать три способа раскрытия этой неопределённости.
то можно использовать три способа раскрытия этой неопределённости.




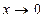




 II. Если
II. Если  то можно использовать три способа раскрытия этой неопределённости.
то можно использовать три способа раскрытия этой неопределённости.

 [
[  -бесконечно малые величины ]=
-бесконечно малые величины ]= 

 и на бесконечности
и на бесконечности 
 где C-const?
где C-const?



 a,b-постоянные
y=x.
a,b-постоянные
y=x.

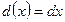










 , a -число
, a -число





 y=ln x
y=ln x
















 или
или  следующих функций:
следующих функций:






 сложной функцией от переменной х:
сложной функцией от переменной х:


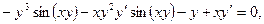










 (2)
(2)



 . Следовательно, чтобы найти у", надо найти дифференциал dy':
. Следовательно, чтобы найти у", надо найти дифференциал dy': 

 при
при  исходя из ее точного значения при
исходя из ее точного значения при 
 представляет собой главную часть приращения этой функции
представляет собой главную часть приращения этой функции  .Если приращение аргумента
.Если приращение аргумента  мало по абсолютной величине, то приращение
мало по абсолютной величине, то приращение  . Так как
. Так как  , а
, а  то имеет место приближенное равенство:
то имеет место приближенное равенство:
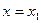 ,
, 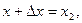 т. е.
т. е. 

 , если известно значение функции и ее производной при
, если известно значение функции и ее производной при  Прежде чем воспользоваться приближенным равенством (1), находим числовое значение производной f'(x) при х= 6:
Прежде чем воспользоваться приближенным равенством (1), находим числовое значение производной f'(x) при х= 6:
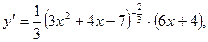 или
или 









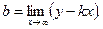
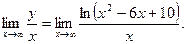








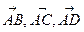 в системе орт
в системе орт 
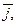
 и найти модули этих векторов;
и найти модули этих векторов;
 на вектор
на вектор 
 а) x0=2; б) x0= -1; в) x0= ¥
а) x0=2; б) x0= -1; в) x0= ¥
 a) x0= -1; б) x0=1; в) x0=¥.
a) x0= -1; б) x0=1; в) x0=¥.
 а) x0=2; б) x0=-2; в) x0=¥.
а) x0=2; б) x0=-2; в) x0=¥.
 а) x0=1; б) x0=2; в) x0=¥.
а) x0=1; б) x0=2; в) x0=¥.
 а) x0= -2; б) x0= -1; в)= ¥.
а) x0= -2; б) x0= -1; в)= ¥.
 а) x0=-1; б) x0=1; в) x0=¥.
а) x0=-1; б) x0=1; в) x0=¥.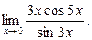
 a) x0=2; б) x0=-2; в) x0= ¥
a) x0=2; б) x0=-2; в) x0= ¥
 a) x0=1; б) x0=2; в) x0=¥.
a) x0=1; б) x0=2; в) x0=¥.
 а) x0= -2; б) x0= -1; в) x0=¥.
а) x0= -2; б) x0= -1; в) x0=¥.
 a) x0= -1; б) x0=1; в) x0= ¥.
a) x0= -1; б) x0=1; в) x0= ¥.
 пользуясь правилами и формулами дифференцирования.
пользуясь правилами и формулами дифференцирования. б)
б) 
 г)
г) 
 б)
б) 
 г)
г) 
 б)
б) 
 г)
г) 
 б)
б) 
 г)
г) 
 б)
б) 
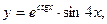 г)
г) 
 б)
б) 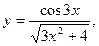
 г)
г) 
 б)
б) 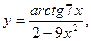
 г)
г) 
 б)
б) 
 г)
г) 
 б)
б) 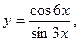
 г)
г) 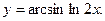
 б)
б) 
 г)
г) 
 a= -1; b= 3;
a= -1; b= 3;
 a= -1; b=2;
a= -1; b=2;
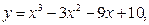 a=2, b=4;
a=2, b=4;
 a= -1, b=2;
a= -1, b=2;
 a=0, b=4;
a=0, b=4;
 a=-2, b=3;
a=-2, b=3;
 a=-3, b=0;
a=-3, b=0;
 a= -3, b=1;
a= -3, b=1;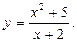
 a=1, b=4;
a=1, b=4;
 a= -1, b=4;
a= -1, b=4;
 (м).
(м).


