Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системы двух уравнений 1-ой степени с двумя переменными. Определители 2-го порядкаСодержание книги
Поиск на нашем сайте
Пусть требуется решить систему
После исключения переменной y из уравнений получим
После исключения переменной x из уравнений получим Если знаменатель Если принять обозначения:
, где Определитель- таблица, составленная из коэффициентов при неизвестных и свободных членов системы (1). Определитель, имеющий две строки и два столбца называется определителем 2-го порядка. Формулы (4) называются формулами Крамера. Вычисление определителей второго порядка: (+)
(-)
Пример:
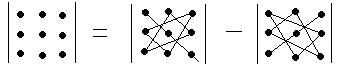
Вычисление определителей 3-го порядка. Правило треугольников
Определитель 3-го порядка равен сумме произведений трёх элементов, взятых по одному из каждой строки и каждого столбца.
Пример. = (-5)-11= -16.
Разложение определителя по элементам 1-ой строки
т.е значение определителя равно произведению элементов 1-ой строки на соответствующие определители 2-го порядка, полученные после вычёркивания i -той строки и k -того столбца, на пересечении которых находится соответствующий элемент, причём a1 берётся со своим знаком, a2 -c противоположным, a3 - со своим знаком. Пример: Вычислить определитель.
-1 2 3 2 1 –3 = -1 3 2 -1
Замечание. Разложение можно выполнять по элементам любой строки (столбца). Задача. Решить систему Решение: Составим главный определитель системы из коэффициентов при неизвестных и вычислим его:
Составим вспомогательный определитель
Составим определитель
Составим определитель
Тогда по правилам Крамера имеем
Сделать проверку самостоятельно. Ответ: x=2, y= -3, z =0
Решение систем линейных уравнений методом Гаусса
Пусть дана система Гаусс при решении системы использовал метод исключения неизвестных. В результате исходная система приводится к треугольному виду:
В этих таблицах, называемых матрицами, должны быть записаны коэффициенты при неизвестных, а после вертикальной черты-свободные члены. В системе (2) из последнего уравнения находится неизвестное z, из 2-го-другое неизвестное y, из 1-го- первое неизвестное x. Задача. Решить систему.
Решение
(первую строку умножаем на (-2) и на (-3) и складываем последовательно со второй и третьей строкой соответственно) ~
(умножаем элементы второй строки на (-8) и складываем с 3-ей строкой). Имеем систему Из этой системы имеем z =0 (из последней строки), y= -3 (из 2-ой строки), x=2 (из 1-ой строки).
Вопросы для самопроверки
|
||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 453; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.008 с.) |

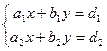 (1)
(1)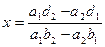 (2).
(2).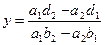 (3)
(3)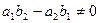 , то система (1) имеет единственное решение, которое находится по формулам (2),(3).
, то система (1) имеет единственное решение, которое находится по формулам (2),(3).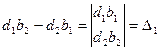

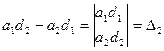
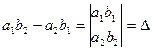 , то решение системы примет вид:
, то решение системы примет вид:  ,
, 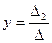 (4)
(4)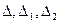 - определители системы,
- определители системы, 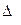 - главный определитель.
- главный определитель.
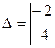
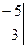 =(-2·3)-(4·(-5))= -6+20=14,
=(-2·3)-(4·(-5))= -6+20=14, 
 , т. е
, т. е

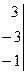 = ((-1)·1·(-1)+2·2·3+2·(-3)·3)-(3.1·3+2·2·(-1)+2·(-3)·(-1))= (1+12-18)- (9-4+6)=
= ((-1)·1·(-1)+2·2·3+2·(-3)·3)-(3.1·3+2·2·(-1)+2·(-3)·(-1))= (1+12-18)- (9-4+6)= =
= 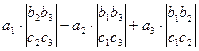

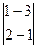 -2
-2 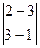 +3
+3 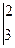
 = -1·(-1+6)-2(-2+9)+3(4-3)= -1·5-2·7+3·1= -16
= -1·(-1+6)-2(-2+9)+3(4-3)= -1·5-2·7+3·1= -16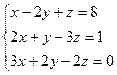


 = 1·
= 1· 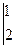
 - (-2)
- (-2) 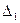 . Он получается из главного путём замены первого столбца свободными членами.
. Он получается из главного путём замены первого столбца свободными членами.

 , путём замены 2-го столбца (в главном определителе) свободными членами.
, путём замены 2-го столбца (в главном определителе) свободными членами.

 путём замены 3-го столбца (в главном определителе) свободными членами.
путём замены 3-го столбца (в главном определителе) свободными членами.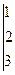
 =0 Вычислить самостоятельно.
=0 Вычислить самостоятельно.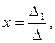
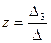 или
или 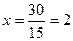 ,
, 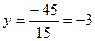 ,
, 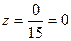
 (1)
(1)

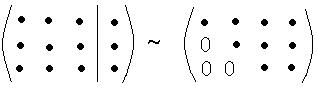

 ~
~ 


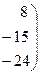 ~
~

 ~
~