
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 3. Основы векторной алгебрыСодержание книги
Поиск на нашем сайте
Ефимов, гл. 7,8 Клетенник, гл. 8,9; Данко, гл. 2.
3.1 Операции над векторами 1.
или
-3
1) 2) 3) 4) Свойства: 1). 2).
3). 4). 5).
6). Угол между векторами:
7). 8). 9).
удовлетворяет условиям:
1).
3).
Свойства: 1). 2). 3). 4). Если 5). 6). Если 7.)
8). 9).
1). 2). 3). Если 4). 5).
Д1 С1
М A1
Д С
А
3. 2 Примеры решения задач Задача 5. Даны координаты вершин пирамиды ABCD: А (2; 1; 0), B (3; -1; 2), С (13; 3; 10), D (0; 1; 4). Требуется: 1) записать векторы
Решение. I. Произвольный вектор а может быть представлен в системе орт i, j, k
где ах, ау, аг — проекции вектора а на координатные оси Ох, Оу и Oz, а
Тогда
Подставив в (3) координаты точек A и В, получим вектор
Аналогично, подставляя в (3) координаты точек А и С, находим
Подставив в (3) координаты точек А и D, находим вектор
Если вектор
Применяя (4), получим модули найденных векторов:
2. Косинус угла между двумя векторами равен скалярному произведению этих векторов, деленному на произведение их модулей. Находим скалярное произведение векторов
Модули этих векторов уже найдены:
3. Проекция вектора
4. Площадь грани ABC равна половине площади параллелограмма, построенного на векторах _
5. Объем параллелепипеда, построенного на трех некомпланарных векторах, равен абсолютной величине их смешанного произведения. Вычислим смешанное произведение
Следовательно, объем параллелепипеда равен 144 куб. ед., а объем заданной пирамиды ABCD равен 24 куб. ед.
3. 3 Вопросы для самопроверки
Тема 4. Введение в анализ. Пискунов, гл 1, § 1-9, упр 1-9, 39, 40 Гл 2, § 1-5, упр 1-6, 9-29, § 6-8, Упр 31-35, 41-48, § 9, 10, упр 57-59 § 11, упр 60-62.
Понятие предела Определение. Число а называется пределом функции y =f(x) в т. Этот факт записывается так: Если Если Если
Если
Если
При вычислении пределов используются теоремы о пределах, а также 1-ый замечательный предел второй замечательный предел
4.2 Способы раскрытия неопределённостей вида
I. Если 1-ый способ. Разложить и числитель и знаменатель дроби на множители, затем сократить на общий множитель.
Пример
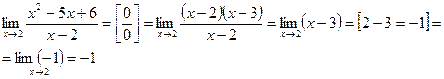
Ответ: где 2- предельное значение аргумента, (-1) -
предельное значение функции y.
2-ой способ. Использовать правило Лопиталя, т.е использовать равенство:
Пример: 3-ий способ. Применить таблицу эквивалентности бесконечно малых.
Таблица.
1.
2.
3.
4.
Пример: Найти
Решение.
1-ый способ. Использовать правило Лопиталя.
Пример. Найти
Решение: 2-ой способ. Разделить все слагаемые числителя и все слагаемые знаменателя на старшую переменную дроби. Пример. Найти Ответ:
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 273; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.123.56 (0.01 с.) |

 - направленный отрезок.
- направленный отрезок.











 Þ | | |
Þ | | |

 Þ | | |
Þ | | |

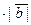

 )
)



 -скалярное произведение векторов, заданных координатами.
-скалярное произведение векторов, заданных координатами. cos j=
cos j=  (проекция вектора
(проекция вектора  =
= 
 =
=  ,
,  , где
, где 
 или
или  -условие коллинеарности векторов.
-условие коллинеарности векторов.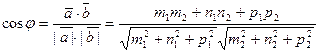 ,
,  - условие перпендикулярности двух векторов.
- условие перпендикулярности двух векторов.






 и
и 
 2).
2). 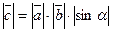

 -образуют такую же ориентацию как
-образуют такую же ориентацию как 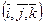
 =
= 
 , где
, где 

 то
то 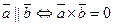

 , то
, то 
 - площадь параллелограмма.
- площадь параллелограмма. -площадь треугольника.
-площадь треугольника.




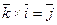
 -форма записи смешанного произведения.
-форма записи смешанного произведения. =
= 
 -компланарны, то
-компланарны, то 


 , если
, если 


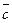 В1
В1

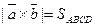


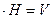 , где V-объём параллелепипеда.
, где V-объём параллелепипеда.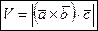
 и
и  в системе орт
в системе орт  и найти модули этих векторов; 2) найти угол между векторами
и найти модули этих векторов; 2) найти угол между векторами  ; 3) найти проекцию вектора
; 3) найти проекцию вектора  следующей формулой;
следующей формулой; (1)
(1)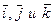 — единичные векторы, направления которых совпадают с положительным направлением осей Ох, Оу и Oz. Если даны точки
— единичные векторы, направления которых совпадают с положительным направлением осей Ох, Оу и Oz. Если даны точки  и
и  то проекции вектора
то проекции вектора  на координатные оси находятся по формулам:
на координатные оси находятся по формулам: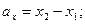

 (2)
(2) (3)
(3)

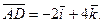
 (4)
(4)
 ,
, 

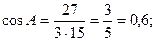
 ¢.
¢.
 . Тогда, как известно, модуль вектора
. Тогда, как известно, модуль вектора 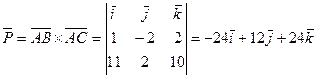

 кв. ед.
кв. ед.

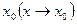 если для любого сколько угодно малого наперёд заданного ε>0 найдётся такое δ>0 (δ=δ(ε)), что выполняется неравенство
если для любого сколько угодно малого наперёд заданного ε>0 найдётся такое δ>0 (δ=δ(ε)), что выполняется неравенство  <e при
<e при  <
< 

 , то функцию
, то функцию  называют бесконечно большой величиной в окрестности т.
называют бесконечно большой величиной в окрестности т. 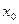 .
. , то
, то  - бесконечно малая функция (величина) в окрестности т. X0.
- бесконечно малая функция (величина) в окрестности т. X0.
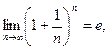
 , а также формулы
, а также формулы  ,
, 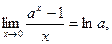

 и
и  .
. то можно использовать три способа раскрытия этой неопределённости.
то можно использовать три способа раскрытия этой неопределённости.




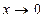




 II. Если
II. Если  то можно использовать три способа раскрытия этой неопределённости.
то можно использовать три способа раскрытия этой неопределённости.

 [
[  -бесконечно малые величины ]=
-бесконечно малые величины ]= 




