Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 2. Элементы аналитической геометрии на плоскостиСодержание книги
Поиск на нашем сайте
Ефимов, гл 1-3, 4-6 Данко, гл. 1, §1-5.
2.1 Основные формулы аналитической геометрии
2.
3.
b
рис 1. рис 2.
4.
M0
рис 3. 5. 6.
y
x
рис 4.
7.
x
М0
рис. 5
8. 9.
y
b
0 a x
рис. 6
10. ß
рис. 7
12. Каноническое уравнение эллипса.
13. Каноническое уравнение гиперболы.
14. Каноническое уравнение параболы.
2.2 Примеры решения задач Задача 1. Даны координаты вершин треугольника А ВС: А (4; 3), В (16; - 6), С (20; 16). Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и ВС и их угловые коэффициенты; 3) угол В в радианах с точностью до двух знаков; 4) уравнение высоты CD и ее длину; 5) уравнение медианы АЕ и координаты точки К пересечения этой медианы с высотой CD; 6) уравнение прямой, проходящей через точку Кпараллельно стороне АВ; 7) координаты точки М, расположенной симметрично точке А относительно прямой CD.
Решение. 1. Расстояние d между точками А (x1; y1) и В (х2; y2) определяется по формуле:
Применяя (1), находим длину стороны АВ:
2. Уравнение прямой, проходящей через точки А(х1; у1) и В(х2; y2), имеет вид:
Подставляя в (2) координаты точек A и В, получим уравнение стороны АВ:
3x+4y-24=0 (AB). Решив последнее уравнение относительно у, находим уравнение стороны АВ в виде уравнения прямой с угловым коэффициентом: 4y= -3x+24; Подставив в (2) координаты точек В и С, получим уравнение прямой BC:
3. Известно, что тангенс угла
Искомый угол В образован прямыми АВ и ВС, угловые коэффициенты которых найдены:
4. Уравнение прямой, проходящей через данную точку в заданном направлении, имеет вид: y—y1 = k(x—x1). (4) Высота CD перпендикулярна стороне АВ. Чтобы найти угловой коэффициент высоты CD, воспользуемся условием перпендикулярности прямых. Так как,
Чтобы найти длину высоты CD, определим сперва координаты точки D-~ точки пересечения прямых АВ и CD. Решая совместно систему:
По формуле (1) находим длину высоты CD:
5. Чтобы найти уравнение медианы АЕ, определим сначала координаты точки Е, которая является серединой стороны ВС, применяя формулы деления отрезка на две равные части:
Следовательно,
Подставив в (2) координаты точек А и Е, находим уравнение медианы:
Чтобы найти координаты точки пересечения высоты CD и медианы АЕ, решим совместно систему уравнений:
6. Так как искомая прямая параллельна стороне АВ, то ее угловой коэффициент будет равен угловому коэффициенту прямой АВ. Подставив в (4) координаты найденной точки К и угловой коэффициент
7. Так как прямая АВ перпендикулярна прямой CD, то искомая точка М, расположенная симметрично точке А относительно прямой CD, лежит на прямой АВ. Кроме того, точка D является серединой отрезка AM. Применяя формулы (5), находим координаты искомой точки М:
Треугольник ABC, высота CD, медиана АЕ, прямая KF и точка М построены в системе координат хОу на рис. 1.
рис. 1
Задача 2. Составить уравнение геометрического места точек, отношение расстояний которых до данной точки A (4; 0) и до данной прямой х=1 равно 2.
Решение.

рис. 2 В системе координат хОу построим точку A (4;0) и прямую х=1. Пусть М(х; у) —произвольная точка искомого геометрического места точек. Опустим перпендикуляр MB на данную прямую х=1 и определим координаты точки В. Так как точка В лежит на заданной прямой, то ее абсцисса равна 1. Ордината точки В равна ординате точки М. Следовательно, В(1,у) (рис. 2). По условию задачи МА:МВ= 2. Расстояния МА и MB находим по формуле (1) задачи 1:
Возведя в квадрат левую и правую части, получим:
Полученное уравнение представляет собой гиперболу, у которой действительная полуось а=2, а мнимая - Определим фокусы гиперболы. Для гиперболы выполняется равенство Определим эксцентриситет полученной гиперболы:
Уравнения асимптот гиперболы имеют вид Следовательно, Задача 3. Составить уравнение геометрического места точек, равноудаленных от точки A (4; 3) и прямой у=1. Полученное уравнение привести к простейшему виду.
Решение.
рис. 3
Пусть М(х; у) — одна из точек искомого геометрического места точек. Опустим из точки М перпендикуляр MB на данную прямую у=1 (рис. 3). Определим координаты точки В. Очевидно, что абсцисса точки В равна абсциссе точки М, а ордината точки В равна I, т. е. В (х; 1). По условию задачи МА=МВ. Следовательно, для любой точки М(х; у), принадлежащей искомому геометрическому месту точек, справедливо равенство:
или
Полученное уравнение определяет параболу с вершиной в точке О¢ (4; 2). Чтобы уравнение параболы привести к простейшему виду, положим x- 4=Х и y+2=Y; тогда уравнение параболы принимает вид:
Чтобы построить найденную кривую, перенесем начало координат в точку О' (4; 2), построим новую систему координат XO'Y, оси которой соответственно параллельны осям Ох и Оу, и затем в этой новой системе построим параболу (*) (рис. 3).
2.3 Вопросы для самопроверки
к каноническому виду. Назовите центр и радиус данной окружности.
|
||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 333; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.48.105 (0.006 с.) |

 1.
1.  - длина отрезка между точками
- длина отрезка между точками  и
и 
 ;
;  - координаты точки деления отрезка в данном отношении.
- координаты точки деления отрезка в данном отношении.

 | | | | |
| | | | |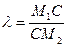 -отношение величины отрезка от начала отрезка т. M1 до делящей т. C к величине отрезка от делящей точки C до конца отрезка M2 .
-отношение величины отрезка от начала отрезка т. M1 до делящей т. C к величине отрезка от делящей точки C до конца отрезка M2 . - уравнение прямой линии с угловым коэффициентом.
- уравнение прямой линии с угловым коэффициентом. - угловой коэффициент прямой.
- угловой коэффициент прямой. - тангенс угла между двумя прямыми.
- тангенс угла между двумя прямыми. -угол между двумя прямыми.
-угол между двумя прямыми. - условие | | двух прямых.
- условие | | двух прямых. - условие ^ двух прямых.
- условие ^ двух прямых.
 y y
y y


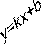


 x x 0 0
x x 0 0
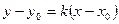 - уравнение пучка прямых.
- уравнение пучка прямых.



 y
y
 - центр пучка.
- центр пучка.
 х
х - уравнение прямой, проходящей через две точки
- уравнение прямой, проходящей через две точки  и
и 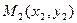
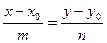 - уравнение прямой, проходящей через точку
- уравнение прямой, проходящей через точку 
 +
+ 

 - уравнение прямой, проходящей через т.
- уравнение прямой, проходящей через т.  .
. y
y
 - общее уравнение прямой- уравнение первой степени с двумя неизвестными.
- общее уравнение прямой- уравнение первой степени с двумя неизвестными. - уравнение в отрезках на осях.
- уравнение в отрезках на осях.
 параметрические уравнения прямой.
параметрические уравнения прямой. , t- переменный параметр.
, t- переменный параметр.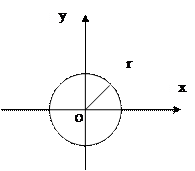 11.
11.  - уравнение окружности с центром в т. O (0;0) и радиусом r. (рис. 7)
- уравнение окружности с центром в т. O (0;0) и радиусом r. (рис. 7) 

 - уравнение окружности со смещённым центром
- уравнение окружности со смещённым центром  . (рис. 8)
. (рис. 8)
 - уравнение эллипса с центром в начале координат.
- уравнение эллипса с центром в начале координат.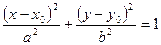 - уравнение эллипса со смещённым центром в т. O1(x0,y0).
- уравнение эллипса со смещённым центром в т. O1(x0,y0).
 - каноническое уравнение гиперболы с центром в начале координат.
- каноническое уравнение гиперболы с центром в начале координат. - уравнение гиперболы со смещённым центром O1 (x0, y0).
- уравнение гиперболы со смещённым центром O1 (x0, y0).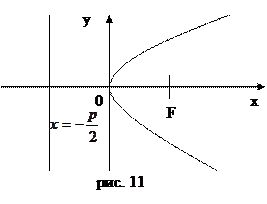
 - каноническое уравнение параболы с вершиной в т. O (0,0).
- каноническое уравнение параболы с вершиной в т. O (0,0).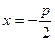 - уравнение директрисы.
- уравнение директрисы.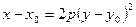 - уравнение параболы со смещённой вершиной в т. O1 (x0,y0)
- уравнение параболы со смещённой вершиной в т. O1 (x0,y0) (1)
(1) =15
=15 (2)
(2)

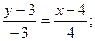 4y-12= -3x+12;
4y-12= -3x+12; откуда
откуда 


 ;
; или y=5,5x-94, откуда kBC=5,5.
или y=5,5x-94, откуда kBC=5,5. между двумя прямыми, угловые коэффициенты которых соответственно равны k1 и k2 вычисляется по формуле:
между двумя прямыми, угловые коэффициенты которых соответственно равны k1 и k2 вычисляется по формуле: (3)
(3)
 Применяя (3), получим
Применяя (3), получим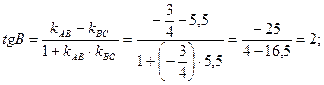 В=63°26'. или В» 1,11 рад.
В=63°26'. или В» 1,11 рад. , то
, то  . Подставив в (4) координаты точки С и найденный угловой коэффициент высоты, получим:
. Подставив в (4) координаты точки С и найденный угловой коэффициент высоты, получим:
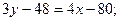

 , находим x=8, y=0, т.е D(8;0)
, находим x=8, y=0, т.е D(8;0)



 E (18;5).
E (18;5).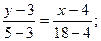


 x=11, y=4; K (11;4).
x=11, y=4; K (11;4). получим:
получим:

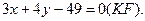









 или
или 

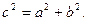 Следовательно, с2=4+12=16; с=4; F 1(— 4; 0), F2(4; 0) — фокусы гиперболы. Как видно, заданная точка A(4; 0) является правым фокусом гиперболы.
Следовательно, с2=4+12=16; с=4; F 1(— 4; 0), F2(4; 0) — фокусы гиперболы. Как видно, заданная точка A(4; 0) является правым фокусом гиперболы.
 и
и 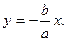
 или
или  и
и  — асимптоты гиперболы. Прежде чем построить гиперболу, строим ее асимптоты.
— асимптоты гиперболы. Прежде чем построить гиперболу, строим ее асимптоты.