
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Первый и второй замечательные пределыСодержание книги
Поиск на нашем сайте
1. Замечание. При x®0 sin x~ x Пример 1.
Найти
если заменить
Заметим,что показатель степени обратен по величине второму слагаемому в основании.
Пример. Выполненные тождественные преобразования в показателе степени, позволяют выделить 2-ой замечательный предел. (в квадратных скобках)
Непрерывность функции. Точки разрыва Определение 1. Функция
Определение 2. Функция где
Пример. Дана функция Требуется: 1). Найти точку разрыва данной функции. 2). Найти 3). Найти скачок функции в точке разрыва. Решение. Данная функция определена и непрерывна в При x=1 функция терпит разрыв, т.к меняется аналитическое выражение функции.
y
x=1- точка разрыва первого рода. Скачком функции называется абсолютная величина разности между её правым и левым предельными значениями т.е Вопросы для самопроверки 1. Дайте определение функции, области определения. Приведите примеры. 2. Сформулируйте определение предела функции в точке. 3. Какая переменная величина называется бесконечно малой? Бесконечно большой в точке 4. Что означают выражения: 5. Приведите пример бесконечно малой функции в т. x=2 и бесконечно большой функции в этой же точке (аналитический и графический). 6. Каким свойством обладает приращение аргумента и приращение функции, если функция непрерывна в точке x0 ?
Тема 5. Производная и дифференциал функции одного аргумента
Пискунов, гл. III, § 1-26, упр 1-220 Гл. IV, § 1-7, упр 1-55.
Определение производной, дифференциала 1. Определение. Производной первого порядка от функции 2.
3.
Геометрически dy представляет собой приращение ординаты касательной к графику функции в заданной точке.
6.
7. Таблица дифференциалов и производных основных элементарных функций
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 245; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.148.63 (0.007 с.) |

 - первый замечательный предел.
- первый замечательный предел.




 , т.к
, т.к  ,
,  то
то

 представили основание в виде суммы 1 и некоторой бесконечно малой величины.
представили основание в виде суммы 1 и некоторой бесконечно малой величины. называется непрерывной в точке x0, если выполняется равенство:
называется непрерывной в точке x0, если выполняется равенство: 

 соответственно приращение аргумента и приращение функции.
соответственно приращение аргумента и приращение функции.

 и
и 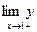





 (ед). –скачок функции.
(ед). –скачок функции. и на бесконечности
и на бесконечности 
 где C-const?
где C-const? по аргументу xназывается предел отношения приращения функции
по аргументу xназывается предел отношения приращения функции  к приращению аргумента
к приращению аргумента 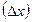 при условии, что
при условии, что  , т.е.
, т.е.  или
или 
 , где a- угол наклона касательной к
, где a- угол наклона касательной к 
 - уравнение касательной, проведённой в т.
- уравнение касательной, проведённой в т. 
 - скорость изменения функции в т. x0.
- скорость изменения функции в т. x0. - дифференциал функции равен произведению производной функции на дифференциал аргумента.
- дифференциал функции равен произведению производной функции на дифференциал аргумента.  - дифференциал аргумента равен приращению аргумента.
- дифференциал аргумента равен приращению аргумента. - дифференциал функции и приращение функции равны лишь приближённо.
- дифференциал функции и приращение функции равны лишь приближённо. - формула для приближённых вычислений.
- формула для приближённых вычислений.



 a,b-постоянные
y=x.
a,b-постоянные
y=x.

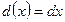










 , a -число
, a -число





 y=ln x
y=ln x



















