
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Криволинейный интеграл II рода. Основные свойства КРИ-II.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Криволинейный интеграл II рода определяется так же, как и интеграл I. Пусть в пространстве
координаты которого – непрерывные функции в точках ориентированной кривой Кривую
Начала этих векторов совпадают с началом элементарных дуг
Предел интегральной суммы, найденный при условии, что
Если функции Основные свойства КРИ-II
1. При изменении направления пути интегрирования криволинейный интеграл II рода изменяет свой знак на противоположный, т.е.
2. Если кривая
Если кривая интегрирования замкнута, криволинейный интеграл II рода обозначается Если плоскую область
где направления обхода по контурам Вычисление КРИ-II: явное представление кривой, параметрическое представ-ление кривой. Некоторые приложения КРИ-II. Вычисление КРИ-II, как и КРИ-I, может быть сведено к вычислению определенного интеграла. Явное представление кривой Если кривая
Параметрическое представление кривой Если гладкая кривая
Если кривая
Площадь плоской фигуры Площадь
при этом кривая Работа переменной силы Переменная сила
|
||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 783; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.206.166 (0.005 с.) |

 (
( ) задан вектор
) задан вектор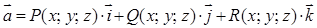 ,
, .
. разобьем в направлении от
разобьем в направлении от  к
к  на
на  элементарных дуг
элементарных дуг  и построим векторы
и построим векторы 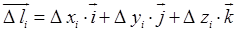 , где
, где  - проекции векторов
- проекции векторов  на оси координат.
на оси координат.
 , а концы – с их концами. На каждой элементарной части
, а концы – с их концами. На каждой элементарной части  и составим интегральную сумму
и составим интегральную сумму .
. , и не зависящий ни от способа разбиения кривой
, и не зависящий ни от способа разбиения кривой  , ни от выбора произвольной точки
, ни от выбора произвольной точки  , называется криволинейным интегралом второго рода (КРИ-II) или криволинейным интегралом по координатам от вектор-функции
, называется криволинейным интегралом второго рода (КРИ-II) или криволинейным интегралом по координатам от вектор-функции  по кривой
по кривой  . Обозначается:
. Обозначается:
 - непрерывны в точках гладкой кривой
- непрерывны в точках гладкой кривой  , то предел интегральной суммы существует, т.е. существует криволинейный интеграл второго рода.
, то предел интегральной суммы существует, т.е. существует криволинейный интеграл второго рода. .
. точкой
точкой  разбита на две части
разбита на две части 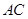 и
и  , то интеграл по всей кривой равен сумме интегралов по ее частям, т.е.
, то интеграл по всей кривой равен сумме интегралов по ее частям, т.е. .
. . В этом случае через кривую
. В этом случае через кривую  проводится ориентированная поверхность и за положительное направление обхода по
проводится ориентированная поверхность и за положительное направление обхода по 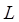 принимается такое направление, при котором область поверхности, ограниченная кривой
принимается такое направление, при котором область поверхности, ограниченная кривой  , ограниченную кривой
, ограниченную кривой  и
и  , то
, то ,
, и задана уравнением
и задана уравнением  , производная
, производная  непрерывна на
непрерывна на  ,
,  , то
, то .
. ,
,  , где
, где  - непрерывно дифференцируемые функции,
- непрерывно дифференцируемые функции,  и
и  - соответственно начальная и конечная точки этой кривой, то верна следующая формула для вычисления КРИ-II:
- соответственно начальная и конечная точки этой кривой, то верна следующая формула для вычисления КРИ-II:

 ,
,  , то формула упрощается
, то формула упрощается

 плоской фигуры, расположенной в плоскости
плоской фигуры, расположенной в плоскости  и ограниченной замкнутой линией
и ограниченной замкнутой линией  ,
, на криволинейном участке
на криволинейном участке 



