
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление двойного интегралаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте В декартовых координатах Покажем, что вычисление двойного интеграла сводится к последовательному вычислению двух определенных интегралов. Пусть требуется вычислить двойной интеграл
направлении оси Построим сечение цилиндрического тела плоскостью, перпендикулярной оси В сечении получаем криволинейную трапецию
Теперь, согласно методу параллельных сечений, искомый объем цилиндрического тела может быть найден так:
С другой стороны, объем цилиндрического тела определяется как двойной интеграл от функции
Таким образом, для вычисления двойного интеграла функции
Правую часть (1.2) называют двукратным (или повторным) интегралом от функции Для вычисления двукратного интеграла сначала берем внутренний интеграл, считая Если область
Вычисление двойного интеграла в полярных координатах. Вычисление двойного интеграла В полярных координатах При вычислении определенного интеграла важную роль играет правило замены переменной, согласно которому при соблюдении соответствующих условий получаем
Обычно функция Для упрощенного вычисления двойного интеграла также применяется метод подстановки. Но правило замены переменной в двойном интеграле значительно сложнее, чем в определенном интеграле. Приведем только окончательную формулу замены переменных в двойном интеграле и разъясним ее на примере преобразования к полярным координатам.
Определим преобразование независимых переменных
Если функции
а функция
Сами новые переменные Функциональный определитель Рассмотрим частный случай замены переменных, часто используемый при вычислении двойного интеграла, а именно замену декартовых координат В качестве переменных Правые части в этих равенствах – непрерывно дифференцируемые функции. Якобиан преобразования определяется как
Формула замены переменных (1.4) принимает вид:
где 5. Приложения двойного интеграла в геометрии и физике. Объем такого цилиндра численно равен площади основания 1. для вычисления в декартовой системе координат: 2. для вычисления в полярной системе координат: Масса плоской фигуры
Согласно физическому смыслу двойного интеграла, масса плоской пластины находится по формуле:
где
|
||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 1269; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.01 с.) |

 , где функция
, где функция  непрерывна в области
непрерывна в области 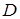 . Тогда, двойной интеграл выражает объем цилиндрического тела, ограниченного сверху поверхностью
. Тогда, двойной интеграл выражает объем цилиндрического тела, ограниченного сверху поверхностью  . Найдем этот объем, используя метод параллельных сечений. Ранее было показано, что
. Найдем этот объем, используя метод параллельных сечений. Ранее было показано, что  , где
, где  - площадь сечения плоскостью, перпендикулярной оси
- площадь сечения плоскостью, перпендикулярной оси  , а
, а  и
и  - уравнения плоскостей, ограничивающих данное тело.
- уравнения плоскостей, ограничивающих данное тело.
 : любая прямая, параллельная оси
: любая прямая, параллельная оси  , где
, где  .
. , ограниченную линиями
, ограниченную линиями  и
и  . Площадь
. Площадь  этой трапеции находим с помощью определенного интеграла:
этой трапеции находим с помощью определенного интеграла: .
. .
.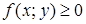 по области
по области  .
. по области
по области  (1.2)
(1.2) по области
по области  . Интеграл
. Интеграл  называется внутренним интегралом.
называется внутренним интегралом. постоянным, затем берем внешний интеграл, т.е. результат первого интегрирования интегрируем по
постоянным, затем берем внешний интеграл, т.е. результат первого интегрирования интегрируем по  в пределах от
в пределах от  до
до  .
. ограничена прямыми
ограничена прямыми  и
и  (
( ), кривыми
), кривыми  и
и 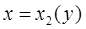 , причем
, причем  для всех
для всех  , т.е. область
, т.е. область  , аналогично получаем
, аналогично получаем
 .
. монотонна. Она осуществляет взаимно однозначное соответствие между точками промежутка
монотонна. Она осуществляет взаимно однозначное соответствие между точками промежутка  изменения переменной
изменения переменной  и точками промежутка
и точками промежутка  изменения переменной
изменения переменной  . Делая замену по формуле
. Делая замену по формуле  , необходимо
, необходимо  заменить на
заменить на  и вместо старых пределов
и вместо старых пределов  и
и 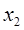 по переменной
по переменной  и
и  по переменной
по переменной  .
. как
как и
и  .
. и
и  имеют в некоторой области
имеют в некоторой области  плоскости
плоскости  непрерывные частные производные первого порядка и отличный от нуля определитель
непрерывные частные производные первого порядка и отличный от нуля определитель ,
, непрерывна в области
непрерывна в области  . (1.4)
. (1.4) и
и  называются криволинейными координатами. Различные системы криволинейных координат играют важную роль в математике и ее приложениях.
называются криволинейными координатами. Различные системы криволинейных координат играют важную роль в математике и ее приложениях. называется определителем Якоби или якобианом (Г. Якоби (1804 – 1851) – немецкий математик).
называется определителем Якоби или якобианом (Г. Якоби (1804 – 1851) – немецкий математик). и
и  .
. ,
,  .
.
 , (1.5)
, (1.5) , т.е. площади области интегрирования
, т.е. площади области интегрирования  ;
; .
. ,
, - плотность этой пластины.
- плотность этой пластины.


