
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление тройного интеграла.Содержание книги
Поиск на нашем сайте
Вычисление тройного интеграла сводится к последовательному вычислению трех определенных интегралов. Пусть областью интегрирования является тело, ограниченное снизу поверхностью
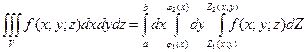 . С помощью этого соотношения и производятся вычисления тройных интегралов. . С помощью этого соотношения и производятся вычисления тройных интегралов.
Пример. Вычислить
Приложения тройного интеграла 1) Объем тела Объем тела V выражается формулой 2) Масса тела Масса тела при заданной плотности 3)Статические моменты Моменты 5) Центр тяжести Координаты центра тяжести тела
V. Числовые ряды Основные понятия Числовым рядом называются выражения вида Рассмотрим частичные суммы Рассмотрим несколько свойств рядов. Свойство 1. Если ряд (1) сходится и его сумма равна Свойство 2. если сходится ряд (1) и сходится ряд Заметим, что сумма (разность) двух расходящихся рядов может быть как сходящимися, так и расходящимися рядами. И из свойства 2 вытекает, что сумма (разность) сходящегося и расходящегося рядов есть ряд расходящийся. Свойство 3. если к ряду (1) прибавить (или отбросить) конечное число членов, то полученный ряд и ряд (1) сходятся или расходятся одновременно. Из этого свойства также следует, что если ряд (1) сходится, то его остаток
|
||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 459; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.54.188 (0.008 с.) |

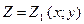 , сверху поверхностью
, сверху поверхностью  , причем
, причем  и
и  (
( , являющейся проекцией тела на плоскость OXY(рис.6). Будем считать область V правильной в направлении оси oz, тогда любая прямая, параллельная оси oz, пересекает границу области не более, чем в двух точках. Тогда для любой непрерывной в области V функции
, являющейся проекцией тела на плоскость OXY(рис.6). Будем считать область V правильной в направлении оси oz, тогда любая прямая, параллельная оси oz, пересекает границу области не более, чем в двух точках. Тогда для любой непрерывной в области V функции  имеет место соотношение
имеет место соотношение  , сводящее вычисление тройного интеграла к вычислению двойного интеграла от однократного (доказательство этого соотношения мы упускаем). При этом сначала вычисляется внутренний интеграл по переменной Z при постоянных х и у в пределах изменения Z. Нижней границей интеграла является аппликата точки А – точки входа прямой, параллельной оси oz, в область V, т.е.
, сводящее вычисление тройного интеграла к вычислению двойного интеграла от однократного (доказательство этого соотношения мы упускаем). При этом сначала вычисляется внутренний интеграл по переменной Z при постоянных х и у в пределах изменения Z. Нижней границей интеграла является аппликата точки А – точки входа прямой, параллельной оси oz, в область V, т.е.  V, т.е.
V, т.е.  ,
, 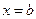 (
( <b),
<b),  и
и  , где
, где  и
и  - непрерывные на отрезке
- непрерывные на отрезке  функции, причем
функции, причем  , где V ограничивается плоскостями
, где V ограничивается плоскостями 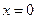 ,
,  ,
,  и
и  (рис.7). Область V является правильной в направлении оси oz (как в направлении ох и оу). Ее проекция на плоскость оху является правильной в направлении оу и ох. Поэтому, применяя выше полученное соотношению имеем
(рис.7). Область V является правильной в направлении оси oz (как в направлении ох и оу). Ее проекция на плоскость оху является правильной в направлении оу и ох. Поэтому, применяя выше полученное соотношению имеем
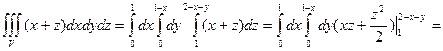



 .
. .
. вычисляется с помощью интеграла (тройного)
вычисляется с помощью интеграла (тройного)  .
. ,
,  ,
,  тела относительно координатных плоскостей OXY, OXZ, OYZ вычисляются по формулам
тела относительно координатных плоскостей OXY, OXZ, OYZ вычисляются по формулам  ,
,  и
и  .
. ,
,  ,
,  .
.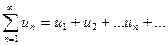 (1), где
(1), где  действительные или комплексные числа, которые называются членами ряда,
действительные или комплексные числа, которые называются членами ряда, 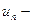 общий член ряда. Этот ряд считается заданным, если известен общий член ряда
общий член ряда. Этот ряд считается заданным, если известен общий член ряда 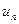 , выраженный как функция его номера
, выраженный как функция его номера  . Сумма первых
. Сумма первых 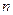 членов ряда называется
членов ряда называется  , т.е.
, т.е. 
 .
. ,
,  ,
,  . Если существует конечный предел
. Если существует конечный предел  последовательности частичных сумм ряда (1), то этот предел называется суммой ряда и говорят, что ряд сходится. Записывают так
последовательности частичных сумм ряда (1), то этот предел называется суммой ряда и говорят, что ряд сходится. Записывают так  . Если
. Если 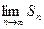 не существует или
не существует или  , то ряд называется расходящимся. Такой ряд суммы не имеет.
, то ряд называется расходящимся. Такой ряд суммы не имеет.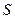 , то ряд
, то ряд  (2), где
(2), где  - произвольное
- произвольное  число также сходится и его сумма равна
число также сходится и его сумма равна  . Если же ряд (1) расходится, то и ряд (2) расходится.
. Если же ряд (1) расходится, то и ряд (2) расходится. , а их суммы равны
, а их суммы равны  и
и 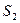 соответственно, то сходятся и ряды
соответственно, то сходятся и ряды 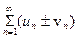 , причем сумма каждого равна соответственно
, причем сумма каждого равна соответственно  .
.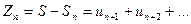 стремится к нулю при
стремится к нулю при  , т.е.
, т.е.  .
.


