
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
II. Система линейных уравнений.Содержание книги
Поиск на нашем сайте Основные понятия Системой m линейных алгебраических уравнений с n неизвестными называется система вида:
Здесь a ij и bj – произвольные числа (i=1,2,3…m; j=1,2,3…n) которые называются соответственно коэффициентами при неизвестных и свободными членами уравнений. хi – неизвестные числа. Такую систему можно записать более кратко с помощью знаков суммирования.
Или в матричной форме: А × Х = В Здесь А – матрица коэффициентов системы называемая основной матрицей.
Х и В представляют собой векторы столбцы, однако в целях единого подхода в рамках матричной алгебры удобнее трактовать их именно как матрицы состоящие соответственно из n и m строк и одного столбца. Произведение матрицы А×Х определено, так как в матрице А столбцов столько же, сколько строк в матрице Х (п – штук). Расширенной матрицей системы называется матрица Ā системы дополняемая столбцом свободных членов.
Решением системы называется п значений неизвестных xj=cj где
Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения. Система совместная называется определенной, если она имеет единственное решение, и неопределенной, ели она имеет более одного решения. В последнем случае каждое её решение называется частным решением системы. Совокупность всех частных решений называется общим решением. Решить систему это, значит, выяснить, совместна она или нет. Если система совместна, то найти её общее решение. Две системы называются эквивалентными, если они имеют одно и тоже общее решение. Другими словами системы эквивалентны, если каждое решение одной является решением другой и наоборот. Эквивалентные системы получаются в частности при элементарных преобразованиях системы при условии, что преобразования выполняются лишь над строками матрицы. Система линейных уравнений называется однородной, если все свободные члены равны 0.
Однородная система всегда совместна так как х1=х2…=хп=0 является решением системы. Это решение называется нулевым или тривиальным. Решение системы линейных уравнений Теорема Кронекера – Капели
Пусть дана произвольная система m линейных уравнений с n неизвестными
Исчерпывающий ответ на вопрос о совместимости этой системы дает теорема Кронекера – Капели (даю без доказательства) Терема 1. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы. Правила практического отыскания всех решений совместной системы линейных уравнений вытекают из следующих теорем. Теорема 2. Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение. Теорема 3. Если ранг совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений. Схема решения произвольной системы линейных уравнений: 1. Найти ранги основной и расширительной матриц системы, если r(A) ≠ r(Ā), то система не совместна. 2. Если r(A) = r(Ā) = r система совместна. Найти какой либо базисный минор порядка r (минор, порядок которого определяет ранг матрицы, называют базисным). Взять r уравнений из коэффициентов, которых составлен базисный минор (остальные уравнения отбросить). Неизвестные, коэффициенты которых входят в базисный минор, называются главными, их оставляют слева, остальные n-r неизвестных называют свободными и переносят в правые части уравнений. 3. Найти выражение главных неизвестных через свободные. Получено общее решение системы. 4. Придавая свободным неизвестным произвольные значения получим соответствующие значения главных неизвестных. Таким образом, можно найти частные решения исходной системы уравнений. Пример:
Таким образом, r(A) ≠ r(Ā), т.е. система не совместна.
|
||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 559; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |



 n
n
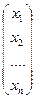 вектор-столбец у неизвестных xj; B =
вектор-столбец у неизвестных xj; B =  вектор-столбец из свободных членов bi.
вектор-столбец из свободных членов bi.

 , при подстановке которых все уравнения системы превращаются в верное равенство (тождество). Всякое решение системы можно записать в виде матрицы-столбца.
, при подстановке которых все уравнения системы превращаются в верное равенство (тождество). Всякое решение системы можно записать в виде матрицы-столбца.
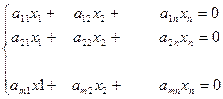
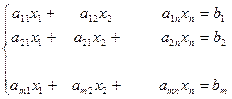

 Решение: A=
Решение: A=  ,r(A)=1 A=
,r(A)=1 A=  ,r(A)=2
,r(A)=2



