
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление длины дуги плоской кривойСодержание книги
Поиск на нашем сайте
 Пусть дана плоская кривая АВ, уравнение которой Пусть дана плоская кривая АВ, уравнение которой  , где , где  (рис.4). Под длиной дуги понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной неограниченно возрастает, а длина наибольшего звена стремится к нулю. Покажем, что если функция (рис.4). Под длиной дуги понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной неограниченно возрастает, а длина наибольшего звена стремится к нулю. Покажем, что если функция  и ее производная и ее производная  непрерывны на отрезке непрерывны на отрезке  , то кривая АВ имеет длину, равную , то кривая АВ имеет длину, равную  . Применим способ №1. Для чего разобьем отрезок . Применим способ №1. Для чего разобьем отрезок  на n частей на n частей  , ,  каждой точке каждой точке  соответствуют точки соответствуют точки  , ,  на кривой АВ. Проведем хорды на кривой АВ. Проведем хорды  , ,  … …  длины которых обозначим соответственно через ∆L1, ∆L2…∆Ln. Получим ломаную линию M0M1…Mn, длина которой равна длины которых обозначим соответственно через ∆L1, ∆L2…∆Ln. Получим ломаную линию M0M1…Mn, длина которой равна 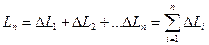 . Длину хорды (или звена ломаной) найдем по теореме Пифагора из треугольника с катетами ∆xi и ∆yi: . Длину хорды (или звена ломаной) найдем по теореме Пифагора из треугольника с катетами ∆xi и ∆yi: 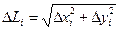 , где , где  , ,  . По теореме Лагранжа о конечном приращении функции . По теореме Лагранжа о конечном приращении функции  . Поэтому . Поэтому  , а длина ломаной линии M0M1…Mn равна , а длина ломаной линии M0M1…Mn равна  (1). (1).
Длина ℓ кривой АВ по определению равна ℓ ℓ Если уравнение кривой задано в параметрической форме Пример: Найти длину окружности радиуса R. Если уравнение окружности записать в параметрической форме Вычисление объема тела а) Вычисление объема тела по известным площадям параллельных сечений.
Через произвольную точку
Пример: Найти объем эллипсоида
Площадь этого эллипса равна б) Объем тела вращения
в) Вычисление координат центра тяжести плоской фигуры
 Пусть дана материальная плоская фигура (пластина), ограниченная кривой Пусть дана материальная плоская фигура (пластина), ограниченная кривой  и прямыми и прямыми  (рис. 8). Будем считать, что плотность пластины (рис. 8). Будем считать, что плотность пластины 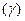 есть величина есть величина  . Тогда масса всей пластины равна . Тогда масса всей пластины равна  , т.е. , т.е.  Выделим элементарный участок пластины в виде бесконечно малой узкой вертикальной полосы и будем считать его прямоугольником. Его масса равна Выделим элементарный участок пластины в виде бесконечно малой узкой вертикальной полосы и будем считать его прямоугольником. Его масса равна  . Центр тяжести прямоугольника лежит на пересечении диагоналей прямоугольника. Это точка . Центр тяжести прямоугольника лежит на пересечении диагоналей прямоугольника. Это точка  отстоит от оси отстоит от оси  на расстоянии на расстоянии  , а от оси , а от оси  на расстоянии на расстоянии  . Тогда для элементарных статистических моментов относительно осей . Тогда для элементарных статистических моментов относительно осей  и и 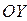 получим следующие соотношения: получим следующие соотношения:  и и  . Отсюда . Отсюда  ; ;  . Если обозначим координаты центра тяжести плоской фигуры . Если обозначим координаты центра тяжести плоской фигуры 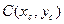 то получим, что то получим, что 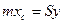 ; ;  , т.е. , т.е. 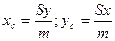 или или  и и  . .
|
||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 510; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.171.72 (0.006 с.) |

 . Заметим, что при
. Заметим, что при  также и
также и  (
(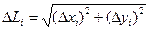 и, следовательно,
и, следовательно,  ). Функция
). Функция  непрерывна на отрезке
непрерывна на отрезке  . Следовательно, существует предел интегральной суммы, когда
. Следовательно, существует предел интегральной суммы, когда 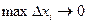 : ℓ
: ℓ  . Таким образом,
. Таким образом, или ℓ
или ℓ  (2).
(2).
 , где x(t) и y(t) – непрерывные функции с непрерывными производными и
, где x(t) и y(t) – непрерывные функции с непрерывными производными и  ,
, 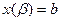 , то длина ℓ находится по формуле: ℓ
, то длина ℓ находится по формуле: ℓ 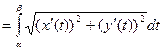 . Это соотношение получается из (2) путем подстановки
. Это соотношение получается из (2) путем подстановки  ,
,  ,
,  .
.
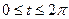 , то ℓ
, то ℓ  .
. Пусть требуется найти объем тела V при известной площади S сечений этого тела относительно плоскости, перпендикулярной некоторой оси, например, ох;
Пусть требуется найти объем тела V при известной площади S сечений этого тела относительно плоскости, перпендикулярной некоторой оси, например, ох;  . Применим метод 2.
. Применим метод 2.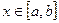 проведем плоскость
проведем плоскость  , перпендикулярную оси ох. Обозначим через
, перпендикулярную оси ох. Обозначим через  площадь сечения тела этой плоскостью.
площадь сечения тела этой плоскостью.  . Через v
. Через v  обозначим объем части тела, лежащие левее плоскости
обозначим объем части тела, лежащие левее плоскости  величина v есть функция от
величина v есть функция от  )=0, v (
)=0, v ( )=v. Теперь найдем дифференциал функции v = v (x). Он представляет собой слой тела, заключенного между параллельными плоскостями, пересекающими ось
)=v. Теперь найдем дифференциал функции v = v (x). Он представляет собой слой тела, заключенного между параллельными плоскостями, пересекающими ось  , который можно приближено принять за цилиндр с основанием
, который можно приближено принять за цилиндр с основанием  (рис.5). поэтому дифференциал объема
(рис.5). поэтому дифференциал объема  . Тогда для нахождения полного объема это соотношение надо проинтегрировать в пределах от
. Тогда для нахождения полного объема это соотношение надо проинтегрировать в пределах от  - полученная формула называется формулой объема тела по площади параллельных сечений.
- полученная формула называется формулой объема тела по площади параллельных сечений. . Если эллипсоид рассечен плоскостью, параллельной плоскости
. Если эллипсоид рассечен плоскостью, параллельной плоскости  и на расстоянии
и на расстоянии 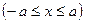 получим эллипс (см. рис. 6).
получим эллипс (см. рис. 6).
 .
. . Поэтому объем эллипсоида
. Поэтому объем эллипсоида 
 Пусть вокруг оси
Пусть вокруг оси  и прямыми
и прямыми  и
и  . Полученная от вращения фигура, называется телом вращения. Сечение этого тела - плоскостью, перпендикулярной оси
. Полученная от вращения фигура, называется телом вращения. Сечение этого тела - плоскостью, перпендикулярной оси 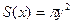 . Поскольку
. Поскольку  - выражение для объема тела вращения вокруг оси
- выражение для объема тела вращения вокруг оси  и прямыми
и прямыми 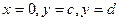 при условии
при условии  , то для объема тела, образованного вращением этой трапеции относительно оси
, то для объема тела, образованного вращением этой трапеции относительно оси  , по аналогии с полученным выше можно записать:
, по аналогии с полученным выше можно записать:



