
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Независимость собственных векторов.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Теорема. Собственные векторы Доказательство. Пусть т.е. при переходе к новому базису собственные числа сохраняются. Наиболее простой вид принимает матрица P линейного оператора
Отсюда следует, что P= Верно и обратное если матрица P линейного оператора Симметричный оператор. Линейный оператор Теорема. Для того, чтобы линейный оператор был симметричен, необходимо и достаточно, чтобы его матрица в ортогональном пространстве была симметрична. Рассмотрим для простоты двухмерное пространство. Линейные операторы
Вычислим векторы
Найдем скалярные произведения
Найдем разность скалярных произведений:
Если эта разность равна 0, то будут выполняться равенства (необходимость)
Ортогональность собственных векторов. Теорема: собственные векторы симметричного линейного оператора, соответствующие различным собственным числам, взаимно ортогональны. Пусть векторы
Квадратичные формы. Пусть L=(
-что является по определению квадратичной формой.
|
|||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 912; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.35.75 (0.011 с.) |

 оператора, отвечающие различным собственным значениям λ1λ2…..λn линейно независимы. Важнейшее следствие: определитель матрицы не зависит от выбора базиса.
оператора, отвечающие различным собственным значениям λ1λ2…..λn линейно независимы. Важнейшее следствие: определитель матрицы не зависит от выбора базиса. - оператор в новом базисе, тогда
- оператор в новом базисе, тогда
 , имеющего n линейно независимых собственных векторов
, имеющего n линейно независимых собственных векторов 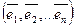 с собственными значениями λ1,λ2…λn.Векторы
с собственными значениями λ1,λ2…λn.Векторы  по базису
по базису  1,
1, 



 если i=j и aij=0 если i ≠ j. Таким образом, в базисе составленном из собственных векторов, матрицы оператора будет иметь диагональный вид.
если i=j и aij=0 если i ≠ j. Таким образом, в базисе составленном из собственных векторов, матрицы оператора будет иметь диагональный вид. =
= 
 и
и  выполняется равенство:
выполняется равенство:  .
. и
и 

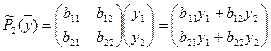
 :
:

 (1)
(1) 11= b11,
11= b11,  ,
, 
 . Подставляя сюда
. Подставляя сюда  и
и  получим
получим  . Вынесем λ1 и λ2 за знак скалярного произведения, перенесем все влево и разложим на множители и получим
. Вынесем λ1 и λ2 за знак скалярного произведения, перенесем все влево и разложим на множители и получим  , так как λ1≠λ2, то
, так как λ1≠λ2, то 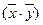 =0, что означает взаимную ортогональность векторов
=0, что означает взаимную ортогональность векторов  )- симметричная матрица n-го порядка, тогда выражение
)- симметричная матрица n-го порядка, тогда выражение  -называется квадратичной формой переменных x1,x2...xn. Матрица L=(
-называется квадратичной формой переменных x1,x2...xn. Матрица L=( =
=  . В матричной форме квадратичная форма имеет вид:
. В матричной форме квадратичная форма имеет вид: , где X=
, где X=  -матрица столбец переменных, а
-матрица столбец переменных, а  =
=  - матрица строка этих же переменных. Найдем произведение этих матриц.
- матрица строка этих же переменных. Найдем произведение этих матриц.





