
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование формы гиперболы по ее уравнениюСодержание книги
Поиск на нашем сайте 1.Уравнение гиперболы содержит x и y в четной степени. Следовательно гипербола симметрична относительно осей Ox и Oy, а также т.O, которую называют центром гиперболы. 2.Найдем точки пересечения гиперболы с осями координат. Положив y=0, находим две точки пересечения гиперболы с осью Ox: A1( Отрезок B1B2 (B1B2=2b), соединяющий точки B1(0,b) и B2(0,-b), называется мнимой полуосью. Прямоугольник со сторонами 2 3. Из уравнения гиперболы следует, что уменьшаемое
     4. Из уравнения гиперболы видно, что когда |x| возрастает, то и |y| возрастает. Это следует из того, что разность 4. Из уравнения гиперболы видно, что когда |x| возрастает, то и |y| возрастает. Это следует из того, что разность  - сохраняет постоянное значение, равное единице. Из всего сказанного следует, что гипербола имеет форму изображенную на рис.4. (кривая, состоящая из двух неограниченных ветвей) - сохраняет постоянное значение, равное единице. Из всего сказанного следует, что гипербола имеет форму изображенную на рис.4. (кривая, состоящая из двух неограниченных ветвей)
Асимптоты гиперболы Прямая L называется асимптотой неограниченной кривой K, если расстояние d от точки M кривой до этой прямой стремится к 0 при неограниченном удалении т.M вдоль кривой K от начала координат. На рис.4 приведена иллюстрация сказанного. Покажем, что гипербола Так как эти прямые и гипербола симметричны относительно осей координат, то достаточно рассмотреть только точки указанных линий, расположенные в первой четверти. Возьмем на прямой И найдем разность MN между ординатами прямой и ветви гиперболы(рис.5)
   
  
При возрастании x знаменатель дроби увеличивается, числитель=const. Стало быть, длинна MN→0, так как MN>d, то и d → 0. То есть Эксцентриситетом гиперболы (
Эксцентриситет характеризует форму гиперболы. Чем меньше эксцентриситет, тем более вытянут ее основной прямоугольник. Гиперболы Парабола Параболой называется множество всех точек плоскости, каждая из которых одинаково удалены от данной точки, называемой фокусом и данной прямой называемой директрисой. Расстояние от фокуса до директрисы называется параметром параболы и обозначается p(p>0). Для вывода уравнения параболы выберем системы координат Oxy так, чтобы ось Ox проходила через F перпендикулярно директрисе в направлении от директрисы к F а начало координат О расположим посредине между фокусом и директрисой(рис.6). В выбранной системе F имеет координаты
      Пусть M(x,y) - произвольная точка параболы. Соединим т.M с F. Проведем отрезок MN перпендикулярный директрисе. Согласно определению параболы MF=MN. По формуле расстояния между точками находим Пусть M(x,y) - произвольная точка параболы. Соединим т.M с F. Проведем отрезок MN перпендикулярный директрисе. Согласно определению параболы MF=MN. По формуле расстояния между точками находим  а а 
 Следовательно Следовательно
Отсюда
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 659; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 ,0),A2(-
,0),A2(-  ,0) называются вершинами гиперболы, а отрезок A1A2=2
,0) называются вершинами гиперболы, а отрезок A1A2=2  не меньше единицы, то есть
не меньше единицы, то есть  или
или 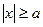 . Это означает, что точки гиперболы расположены справа от прямой x=
. Это означает, что точки гиперболы расположены справа от прямой x= 
 имеет две асимптоты:
имеет две асимптоты:  и
и 




 - асимптоты гиперболы.
- асимптоты гиперболы. ) называется отношение расстояния между фокусами к величине действительной оси гиперболы:
) называется отношение расстояния между фокусами к величине действительной оси гиперболы: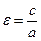 ,т.к. с>a, то
,т.к. с>a, то 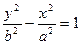 имеют общие асимптоты, такие гиперболы называются сопряженными.
имеют общие асимптоты, такие гиперболы называются сопряженными. , а уравнение директрисы имеет вид
, а уравнение директрисы имеет вид  или
или 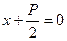 .
.

 Возводя в квадра
Возводя в квадра  т
т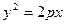 - каноническое уравнение параболы.
- каноническое уравнение параболы.


