
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегральный признак Коши. Обобщенный гармонический рядСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Теорема. Если члены знакоположительного ряда 1) 2) если Рассмотрим криволинейную трапецию, ограниченную сверху графиком функции Случай 1. Несобственный интеграл Случай 2. Несобственный интеграл Пример. Исследовать на сходимость ряд Рассмотренные признаки сходимости знакоположительных рядов позволяют судить о сходимости практически любого положительного ряда.
Знакочередующиеся и знакопеременные ряды Признак Лейбница Рассмотрим важный класс рядов, называемых знакочередующимися. Такими рядами называется ряд вида: Теорема Лейбница. Знакочередующийся ряд сходится, если: 1) последовательность абсолютных величин членов ряда монотонно убывает, т.е. 2) общий член ряда стремится к нулю Доказательство: Рассмотрим сначала частичную сумму четного числа С другой стороны Рассмотрим теперь частичные суммы нечетного числа Замечания. 1) Исследование знакочередующихся рядов вида 2) Соотношение Пример. Вычислить сумму ряда
Общий достаточный признак сходимости знакопеременных рядов
Знакочередующийся ряд является частным случаем знакопеременного ряда. Числовой ряд Теорема. Пусть дан знакопеременный ряд Доказательство: Рассмотри вспомогательный ряд, составленный из членов рядов
Очевидно, что Отметим, что обратное утверждение несправедливо: если сходится ряд Пример. Исследовать сходимость ряда
|
||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 905; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.79.165 (0.011 с.) |

 могут быть представлены как числовые значения некоторой непрерывно монотонно убывающей на промежутке
могут быть представлены как числовые значения некоторой непрерывно монотонно убывающей на промежутке  функции
функции 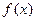 так, что
так, что  то
то если
если  сходится, то сходится и ряд
сходится, то сходится и ряд 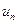 .
. , основанием которой служит отрезок оси
, основанием которой служит отрезок оси  от
от  до
до  (рис.1). Построим входящие и выходящие прямоугольники, основаниями которых служат отрезки
(рис.1). Построим входящие и выходящие прямоугольники, основаниями которых служат отрезки  … Учитывая геометрический смысл определенного интеграла можно записать
… Учитывая геометрический смысл определенного интеграла можно записать  или
или  или
или  (1).
(1).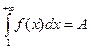 . Поскольку
. Поскольку  <
<  , то с учетом неравенства (1) имеем
, то с учетом неравенства (1) имеем  , т.е.
, т.е.  .Так как последовательность частичных сумм монотонно возрастает и ограничена сверху (числом
.Так как последовательность частичных сумм монотонно возрастает и ограничена сверху (числом  ), то по признаку существования предела, имеет предел. Следовательно, ряд
), то по признаку существования предела, имеет предел. Следовательно, ряд  и интеграл
и интеграл 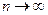 . Учитывая, что
. Учитывая, что  (см. 1) получаем, что
(см. 1) получаем, что  при
при  . Воспользуемся интегральным признаком Коши. Функция
. Воспользуемся интегральным признаком Коши. Функция  удовлетворяет условиям теоремы. Поэтому находим
удовлетворяет условиям теоремы. Поэтому находим 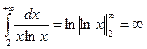 . Значит, ряд с общим членом
. Значит, ряд с общим членом  расходится. Ряд
расходится. Ряд  , где
, где  – действительное число называется обобщенным гармоническим рядом. Для исследования этого ряда на сходимость применим интегральный признак Коши. Рассмотрим функцию
– действительное число называется обобщенным гармоническим рядом. Для исследования этого ряда на сходимость применим интегральный признак Коши. Рассмотрим функцию 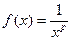 . Эта функция непрерывна, монотонно убывает на промежутке
. Эта функция непрерывна, монотонно убывает на промежутке  и
и  . При
. При  имеем:
имеем:  . При
. При  имеем гармонический ряд
имеем гармонический ряд  , который расходится (второй способ
, который расходится (второй способ  ). Итак, гармонический ряд сходится при
). Итак, гармонический ряд сходится при  , расходится при
, расходится при  .
. , где
, где  для всех
для всех 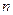 . Для знакочередующихся рядов имеет место достаточный признак сходимости (Признак Лейбница).
. Для знакочередующихся рядов имеет место достаточный признак сходимости (Признак Лейбница).
 . При этом сумма
. При этом сумма 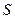 ряда удовлетворяет неравенствам
ряда удовлетворяет неравенствам  .
.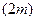 членов ряда. Имеем
членов ряда. Имеем  . Выражения в каждой скобке согласно первому условию теоремы положительно. Следовательно, сумма
. Выражения в каждой скобке согласно первому условию теоремы положительно. Следовательно, сумма  и возрастает с возрастанием номера
и возрастает с возрастанием номера  .
. , можно переписать так:
, можно переписать так:  . Легко увидеть, что
. Легко увидеть, что  . Таким образом, последовательность
. Таким образом, последовательность  возрастает и ограничена сверху. Следовательно, она имеет предел
возрастает и ограничена сверху. Следовательно, она имеет предел  , причем
, причем  членов ряда. Очевидно, что
членов ряда. Очевидно, что  . Отсюда следует, что
. Отсюда следует, что  . Т.к.
. Т.к.  в силу второго условия теоремы. Итак,
в силу второго условия теоремы. Итак,  как при четном
как при четном  (с отрицательным первым членом) сводится путем умножения всех его членов на (-1) к исследованию ряда с + первым членом.
(с отрицательным первым членом) сводится путем умножения всех его членов на (-1) к исследованию ряда с + первым членом. . Отброшенный ряд представляет собой также знакочередующийся ряд, сумма которого по модулю меньше первого члена этого ряда, т.е.
. Отброшенный ряд представляет собой также знакочередующийся ряд, сумма которого по модулю меньше первого члена этого ряда, т.е. 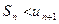 поэтому ошибка меньше модуля первого из отброшенных членов.
поэтому ошибка меньше модуля первого из отброшенных членов. . Данный ряд лейбницевского вида. Он сходится. Можно записать
. Данный ряд лейбницевского вида. Он сходится. Можно записать  . Взяв 5 членов, т.е. заменив
. Взяв 5 членов, т.е. заменив  сделаем ошибку, меньшую чем
сделаем ошибку, меньшую чем  . Итак,
. Итак,  .
.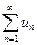 , содержащий бесконечное множество положительных и бесконечных множеств отрицательных членов, называется знакопеременным. Для знакопеременных рядов имеет место следующий общий достаточный признак сходимости.
, содержащий бесконечное множество положительных и бесконечных множеств отрицательных членов, называется знакопеременным. Для знакопеременных рядов имеет место следующий общий достаточный признак сходимости. . Если сходится ряд
. Если сходится ряд  , составленный из модулей членов данного ряда, то сходится и сам знакопеременный ряд.
, составленный из модулей членов данного ряда, то сходится и сам знакопеременный ряд. .
. .
. для всех
для всех  сходится в силу условий теоремы и свойства 1 числовых рядов. Следовательно, на основании признака сравнения сходится и ряд
сходится в силу условий теоремы и свойства 1 числовых рядов. Следовательно, на основании признака сравнения сходится и ряд  . Поскольку данный знакопеременный ряд представляет собой разность двух сходящихся рядов
. Поскольку данный знакопеременный ряд представляет собой разность двух сходящихся рядов  , то на основании свойства 2 числовых рядов ряд
, то на основании свойства 2 числовых рядов ряд  .
. . Для этого ряда выполнены условия признака Лейбница. Следовательно, ряд сходится. Однако ряд, составленный из модулей членов этого ряда, т.е.
. Для этого ряда выполнены условия признака Лейбница. Следовательно, ряд сходится. Однако ряд, составленный из модулей членов этого ряда, т.е. 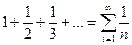 расходится (гармонический ряд).
расходится (гармонический ряд).


