
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: «Описательная статистика. Показатели разнообразия признака в совокупности»Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Основными критериями разнообразия признака в статистической совокупности являются: лимит, амплитуда, среднее квадратическое отклонение, коэффициент осцилляции и коэффициент вариации. На предыдущем занятии обсуждалось, что средние величины дают лишь обобщающую характеристику изучаемого признака в совокупности и не учитывают значения отдельных его вариант: минимальное и максимальное значения, выше среднего, ниже среднего и т.д. Пример. Средние величины двух разных числовых последовательностей: -100; -20; 100; 20 и 0,1; -0,2; 0,1 абсолютно одинаковы и равны О. Однако, диапазоны разброса данных этих последовательностей относительного среднего значения сильно различны. Определение перечисленных критериев разнообразия признака прежде всего осуществляется с учетом его значения у отдельных элементов статистической совокупности. Показатели измерения вариации признака бывают абсолютные и относительные. К абсолютным показателям вариации относят: размах вариации, лимит, среднее квадратическое отклонение, дисперсию. Коэффициент вариации и коэффициент осцилляции относятся к относительным показателям вариации. Лимит (lim)– это критерий, который определяется крайними значениями вариант в вариационном ряду. Другими словами, данный критерий ограничивается минимальной и максимальной величинами признака:
Амплитуда (Am) или размах вариации – это разность крайних вариант. Расчет данного критерия осуществляется путем вычитания из максимального значения признака его минимального значения, что позволяет оценить степень разброса вариант:
Недостатком лимита и амплитуды как критериев вариабельности является то, что они полностью зависят от крайних значений признака в вариационном ряду. При этом не учитываются колебания значений признака внутри ряда.
Наиболее полную характеристику разнообразия признака в статистической совокупности дает среднее квадратическое отклонение В основе среднего квадратического отклонения лежит сопоставление каждой варианты
По смыслу, дисперсия – это средний квадрат отклонений индивидуальных значений признака от его средней величины. Дисперсия – квадрат среднего квадратического отклонения Дисперсия является размерной величиной (именованной). Так, если варианты числового ряда выражены в метрах, то дисперсия дает квадратные метры; если варианты выражены в килограммах, то дисперсия дает квадрат этой меры (кг2), и т.д. Среднее квадратическое отклонение – квадратный корень из дисперсии:
В том случае, если число элементов совокупности Расчет среднего квадратического отклонения можно разбить на шесть этапов, которые необходимо осуществить в определенной последовательности: 1. определить среднюю арифметическую M имеющейся совокупности 2. рассчитать отклонение каждой варианты от средней величины: 3. каждое отклонение возвести в квадрат: 4. посчитать сумму всех 5. разделить получившуюся сумму на число элементов совокупности n 6. из полученного результата извлечь квадратный корень Применение среднеквадратического отклонения: а) для суждения о колеблемости вариационных рядов и сравнительной оценки типичности (представительности) средних арифметических величин. Это необходимо в дифференциальной диагностике при определении устойчивости признаков. б) для реконструкции вариационного ряда, т.е. восстановления его частотной характеристики на основе правила «трех сигм». В интервале (М±3σ) находится 99,7% всех вариант ряда, в интервале (М±2σ) — 95,5% и в интервале (М±1σ) — 68,3% вариант ряда (рис.1). в) для выявления «выскакивающих» вариант г) для определения параметров нормы и патологии с помощью сигмальных оценок д) для расчета коэффициента вариации е) для расчета средней ошибки средней арифметической величины.
Для характеристики любой генеральной совокупности, имеющей нормальный тип распределения, достаточно знать два параметра: среднюю арифметическую и среднее квадратическое отклонение.
Рисунок 1. Правило «трех сигм» Пример. В педиатрии среднеквадратическое отклонение используется для оценки физического развития детей путем сравнения данных конкретного ребенка с соответствующими стандартными показателями. За стандарт принимаются средние арифметические показатели физического развития здоровых детей. Сравнение показателей со стандартами проводят по специальным таблицам, в которых стандарты приводятся вместе с соответствующими им сигмальными шкалами. Считается, что если показатель физического развития ребенка находится в пределах стандарт (среднее арифметическое) ±σ, то физическое развитие ребенка (по этому показателю) соответствует норме. Если показатель находится в пределах стандарт ±2σ, то имеется незначительное отклонение от нормы. Если показатель выходит за эти границы, то физическое развитие ребенка резко отличается от нормы (возможна патология). Кроме показателей вариации, выраженных в абсолютных величинах, в статистическом исследовании используются показатели вариации, выраженные в относительных величинах. Коэффициент осцилляции -это отношение размаха вариации к средней величине признака. Коэффициент вариации - это отношение среднего квадратического отклонения к средней величине признака. Как правило, эти величины выражаются в процентах. Формулы расчета относительных показателей вариации:
Из приведенных формул видно, что чем больше коэффициент V приближен к нулю, тем меньше вариация значений признака. Чем больше V, тем более изменчив признак. В статистической практике наиболее часто применяется коэффициент вариации. Он используется не только для сравнительной оценки вариации, но и для характеристики однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений, близких к нормальному). Арифметически отношение σ и средней арифметической нивелирует влияние абсолютной величины этих характеристик, а процентное соотношение делает коэффициент вариации величиной безразмерной (неименованной). Полученное значение коэффициента вариации оценивается в соответствии с ориентировочными градациями степени разнообразия признака: - слабое — до 10 % - среднее — 10 - 20 % - сильное — более 20 % Использование коэффициента вариации целесообразно в случаях, когда приходится сравнивать признаки разные по своей величине и размерности. Отличие коэффициента вариации от других критериев разброса наглядно демонстрирует пример. Таблица 1 Состав работников промышленного предприятия
На основании приведенных в примере статистических характеристик можно сделать вывод об относительной однородности возрастного состава и образовательного уровня работников предприятия при низкой профессиональной устойчивости обследованного контингента. Нетрудно заметить, что попытка судить об этих социальных тенденциях по среднему квадратическому отклонению привела бы к ошибочному заключению, а попытка сравнения учетных признаков «стаж работы» и «возраст» с учетным признаком «образование» вообще была бы некорректной из-за разнородности этих признаков. Медиана и перцентили Для порядковых (ранговых) распределений, где критерием середины ряда является медиана, среднеквадратическое отклонение и дисперсия не могут служить характеристиками рассеяния вариант. То же свойственно и для открытых вариационных рядов. Указанное обстоятельство связано с тем, что отклонения, по которым вычисляются дисперсия и σ, отсчитываются от среднего арифметического, которое не вычисляется в открытых вариационных рядах и в рядах распределений качественных признаков. Поэтому для сжатого описания распределений используется другой параметр разброса – квантиль (синоним - «nерцентиль»), пригодный для описания качественных и количественных признаков при любой форме их распределения. Этот параметр может использоваться и для перевода количественных признаков в качественные. В этом случае такие оценки присваиваются в зависимости от того, какому по порядку квантилю соответствует та или иная конкретная варианта. В практике медико-биологических исследований наиболее часто используются следующие квантили:
Квантили делят область возможных изменений вариант в вариационном ряду на определенные интервалы. Медиана (квантиль В случае асимметричности распределения переменной относительно среднего арифметического для его характеристики используются медиана и квартили. В этом случае используется следующая форма отображения средней величины – Ме (
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 807; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.19.89 (0.008 с.) |

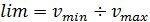

 (сигма), которое является общей мерой отклонения вариант от своей средней величины. Среднее квадратическое отклонение часто называют также стандартным отклонением.
(сигма), которое является общей мерой отклонения вариант от своей средней величины. Среднее квадратическое отклонение часто называют также стандартным отклонением. со средней арифметической
со средней арифметической  данной совокупности. Так как в совокупности всегда будут варианты как меньше, так и больше, чем она, то сумма отклонений
данной совокупности. Так как в совокупности всегда будут варианты как меньше, так и больше, чем она, то сумма отклонений  , имеющих знак "
, имеющих знак "  ", будет погашаться суммой отклонений, имеющих знак "
", будет погашаться суммой отклонений, имеющих знак "  ", т.е. сумма всех отклонений
", т.е. сумма всех отклонений  равна нулю. Для того, чтобы избежать влияния знаков разностей берут отклонения вариант от среднего арифметического в квадрате, т.е.
равна нулю. Для того, чтобы избежать влияния знаков разностей берут отклонения вариант от среднего арифметического в квадрате, т.е.  . Сумма квадратов отклонений не равняется нулю. Чтобы получить коэффициент, способный измерить изменчивость, берут среднее от суммы квадратов – это величина носит название дисперсии:
. Сумма квадратов отклонений не равняется нулю. Чтобы получить коэффициент, способный измерить изменчивость, берут среднее от суммы квадратов – это величина носит название дисперсии: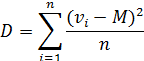
 .
.
 , то при расчете дисперсии и среднего квадратического отклонения в знаменателе дроби вместо
, то при расчете дисперсии и среднего квадратического отклонения в знаменателе дроби вместо  необходимо ставить
необходимо ставить  .
.
 (Для получения обобщающей характеристики числового ряда использовать сумму отклонений от среднего нельзя. Это связано с тем, что сумма всех отрицательных и положительных отклонений от среднего всегда равна нулю.)
(Для получения обобщающей характеристики числового ряда использовать сумму отклонений от среднего нельзя. Это связано с тем, что сумма всех отрицательных и положительных отклонений от среднего всегда равна нулю.)


 – медиана;
– медиана; ,
,  – квартили (четверти), где
– квартили (четверти), где  – верхний квартиль.
– верхний квартиль.


