Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Индексы количественных показателейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Виды степенных средних
.
15. Ошибки наблюдения Расхождение между расчетным и действительным значениями изучаемых величин называется ошибкой наблюдения. В зависимости от причин возникновения различают: - ошибки регистрации; - ошибки репрезентативности. Ошибка регистрации - это отклонения между значением показателя, полученного в ходе статистического наблюдения, и фактическим, действительным его значением. Этот вид ошибок может быть и при сплошном, и при несплошном наблюдении. Ошибки регистрации бывают - случайные и систематические. Случайные ошибки - это результат действия различных факторов (например, цифры переставлены местами, перепутаны графы при заполнении формуляра и т. п.). Систематические ошибки регистрации всегда имеют одинаковую тенденцию либо к увеличению, либо к уменьшению значения показателей по каждой единице совокупности. Примером может служить округление возраста населения при проведении социологических опросов населения. Многие опрашиваемые, например, вместо 48-49 и 51-52 лет говорят, что им 50. Систематические ошибки характерны только для не сплошного наблюдения. Причина их возникновения состоит в том, что отобранная и обследованная совокупность недостаточно точно воспроизводит (репрезентирует) всю исходную совокупность в целом. Отклонение значения показателя обследованной совокупности от его величины по исходной совокупности называется ошибкой репрезентативности. Они также бывают случайные и систематические. Случайные ошибки возникают, если отобранная совокупность неполно воспроизводит всю совокупность в целом. Систематические ошибки репрезентативности появляются вследствие нарушения принципов отбора единиц из исходной совокупности, которые должны быть подвергнуты наблюдению. Чтобы избежать ошибок необходимо: 1) обеспечить качественное обучение персонала, который буде проводить наблюдение; 2) организовать специальные частичные или сплошные контрольные проверки правильности заполнения стат. формуляров; 3) провести логический и арифметический контроль полученных данных после окончания сбора информации. Арифметический контроль основывается на использовании количественных связей между значениями различных показателей. Логический контроль основывается на знании взаимосвязей между логическими показателями. Например, человек в возрасте 6 лет не может иметь высшего образования. Обычно для исправления ошибок, выявленных в ходе логич. контроля, требуется повторно обратиться к источнику сведений.
16. Логический и арифметический контроль 2. Логическим контролем проверяются правильность записи кодов, соответствие их наименованиям и значениям показателей. Выполняется проверка необходимых взаимосвязей между показателями, сопоставляются ответы на различные вопросы и выявляются несовместимые сочетания. Для исправления ошибок, выявленных при логическом контроле, возвращаются к исходным документам и делают поправки. 3. При арифметическом контроле сравниваются полученные итоги с предварительно подсчитанными контрольными суммами по строкам и по графам. Довольно часто арифметический контроль основывается на зависимости одного показателя от двух или нескольких других (например, является произведением других показателей). Если арифметический контроль итоговых показателей обнаружит, что данная зависимость не соблюдается, это будет свидетельствовать о неточности данных. Таким образом, контроль достоверности статистической информации осуществляется на всех этапах проведения статистического наблюдения – начиная со сбора первичной информации и до этапа получения итогов. 17. Теория практики (перспективы развития) Индексный метод систем индексов-индикаторов. Этот метод позволяет оценивать экономическую и социальную конъюнктуру государств, их регионов, отраслей и секторов экономики, а также состояние и перспективы развития предприятий, фирм, учреждений и организаций. С этой целью в масштабах государств используют национальные системы индикаторов и "экономические барометры", на уровне регионов, отраслей и секторов экономики - соответственно региональные, отраслевые и секторные системы индексов-индикаторов, на микроуровне - системы индексов-индикаторов предприятий, фирм, организаций, учреждений, банков, бирж и т.д.. 18. Интернет статистика, статистика времени, качества С тех пор как в конце 90-х годов новорожденный отечественный сервис интернет-статистики сделал свои первые шаги по Рунету, чаша наше-западных весов уверенно сместилась ежели таковые при сем присутствовали. Естественно, деньги (зеленые) и чужой язык (порядки, нравы, спецификация) стали достаточно веским основанием для подобного события. С тех пор через окошко на запад заглядывали только самые упорные и любопытствующие – чтобы слегка присмотреться – а как там дела у них? Как считают, кого считают, что делают с полученными цифрами? Присмотреться, перенять опыт, а если повезет, то и поюзать демо-версию какой-нибудь новой программы. Сегодня фактически каждый пользователь сети Интернет тем или иным образом имеет дело со статистическими системами и услугами. Прямая заинтересованность в них владельцев веб-ресурсов проистекает из практической необходимости качественной и количественной оценки посещаемости сайтов. Если анализировать технологии сбора подобной информации, то вариантов немного. Это либо счетчики – специальные скрипты, загружаемые одновременно с веб-страницей (чаще всего с внешнего, собственно статистического, сервера) либо специальные программы, анализирующие записи в логах (файлах на вашем сервере, фиксирующих все посещения). В принципе, всю эволюцию интернет-статистики как таковой, не важно – на Западе или в Рунете, можно свести всего к двум направлениям – 1) улучшение качества сбора и обработки первичной информации и 2) извлечение максимальной выгоды из собранных данных для повышения успешности маркетинга веб-проектов и, как следствие, доходности интернет-бизнеса. Конечно, эти два направления тесно взаимосвязаны. И в том или ином виде развиваются как у нас, так и у них. Однако пока в Рунете не утихают споры о том, кто лучше/хуже считает, то есть, собственно, о технологии интернет-статистики, Запад, напротив, больше озабочен другой стороной вопроса, собственно вкладом интернет-статистических данных в формирование, контроль и развитие бизнеса. 19. Индексный метод основы Индексный метод - это метод экономического анализа, который основан на относительных показателях, выражающих отношение уровня данного явления к его уровню в предыдущие временные периоды или к уровню аналогичного явления, принятому в качестве базы сравнения. Всякий индекс исчисляется сопоставлением соизмеряемой (отчетной) величины с базисной. Индексы, выражающие соотношение непосредственно соизмеряемых величин, называются индивидуальными, а характеризующие соотношения сложных явлений - групповыми, или тотальными. Индексным методом можно выявить влияние на изучаемый совокупный показатель различных факторов. В статистике известно несколько форм индексов, которые используются в аналитической работе (агрегатная, арифметическая, гармоническая и др.). Агрегатный индекс является основной формой всякого общего индекса. Именно агрегатный индекс можно преобразовать в средний арифметический или средний гармонический индекс. Схема расчета агрегатного индекса следующая:
∑ g1p1 - ∑ g0p0 = (∑ g1p0 - ∑ g0p0) + (∑ g1p1 - ∑ g1p0),
где, (∑ g1p0 - ∑ g0p0) - влияние количества; (∑ g1p1 - ∑ g1p0) – влияние цен.
Здесь следует отметить, что агрегатный индекс является основной основой всякого общего индекса; его можно преобразовать как в средний арифметический, так и в средний гармонический индексы. С помощью индексных пересчетов можно осуществлять преобразование агрегатного индекса в средний гармонический. Способ относительных чисел применяется тогда, когда изучаемый показатель является результатом произведения нескольких факторов. Он отличается от предыдущих тем, что расчеты влияния факторов на изучаемый показатель проводятся исходя из относительных показателей их изменения, выраженных в процентах или коэффициентах. При определении влияния первого фактора процентное выражение изменения его величины, деленное на 100, умножают на базисную величину изучаемого показателя. Для определения влияния второго и каждого последующего фактора сначала устанавливают процентное выражение изменения изучаемого показателя за счет соответствующего фактора с учетом влияния предшествующих факторов и затем умножают его на базисное значение изучаемого показателя. Влияние последнего фактора определяется так: из показателя выполнения плана вычитают совокупный процент влияния всех предшествующих факторов; полученный результат умножают на базисную величину изучаемого показателя и делят на 100. Индексный метод основывается на сопоставлении показателей отчетного и базисного периодов. Основным условием при этом является то, что сопоставляемые величины должны быть идентичны, т. е. рассчитываться одинаково (в одной методологии) или в одних ценах (в ценах базисного или отчетного периода) и обязательно в одних единицах измерения. Индексный метод — один из наиболее распространенных, поскольку с его помощью можно выявить влияние на изучаемый совокупный показатель различных факторов. В практике статистических и аналитических расчетов известно несколько форм индексов: агрегатная, арифметическая, гармоническая и др.
20. Средние линейные уравнения Мудрые математики и статистики придумали более надежный показатель, хотя и несколько другого назначения – среднее линейное отклонение. Этот показатель характеризует меру разброса значений совокупности данных вокруг их среднего значения. В чем суть? Для того, чтобы показать меру разброса данных нужно вначале определиться, относительно чего этот самый разброс будет считаться. Обычно это средняя величина. Дальше нужно посчитать, насколько значения анализируемой совокупности данных находятся далеко от средней. Понятное дело, что каждому значению соответствует некоторая величина отклонения, но нас же интересует общая оценка, охватывающая всю совокупность. Поэтому рассчитывают среднее отклонение по формуле обычной средней арифметической. Но! Но для того, чтобы рассчитать среднее из отклонений, их нужно вначале сложить. И если мы сложим положительные и отрицательные числа, то они взаимоуничтожатся и их сумма будет стремиться к нулю. Чтобы этого избежать, все отклонения берутся по модулю, то есть все отрицательные числа становятся положительными. Вот теперь среднее отклонение будет показывать обобщенную меру разброса значений. В итоге, средне линейное отклонение будет рассчитываться по формуле:
где a – среднее линейное отклонение, x – анализируемый показатель, с черточкой сверху – среднее значение показателя, n – количество значений в анализируемой совокупности данных, Рассчитанное по указанной формуле среднее линейное отклонение отражает среднее абсолютное отклонение от средней величины по данной совокупности. Допустим, имеется фирма по производству черенков для лопат. Каждый черенок должен быть 1,5 метра длиной, но, что еще важней, все должны быть одинаковыми или, по крайней мере, плюс-минус 5 см. Однако нерадивые работники то 1,2 м отпилят, то 1,8 м. Дачники недовольны. Решил директор фирмы провести статистический анализ длины черенков. Отобрал 10 штук и замерял их длину, нашел среднюю и рассчитал среднее линейное отклонение. Средняя получилась как раз, что надо – 1,5 м. А вот среднее линейное отклонение вышло 0,16 м. Вот и получается, что каждый черенок длиннее или короче, чем нужно в среднем на 16 см. Есть, о чем поговорить с работниками. На самом деле я не встречал реального использования данного показателя, поэтому пример придумал сам. Тем не менее, в статистике есть такой показатель.
21. Сторона явления количественных и качественных показателей Интервальные ряды динамики Уровни интервального ряда характеризуют результат изучаемого процесса за период времени: производство или реализация продукции (за год, квартал, месяц и др. периоды), число принятых на работу, число родившихся и.т.п. Уровни интервального ряда можно суммировать. При этом получаем такой же показатель за более длительные интервалы времени. Средний уровень в интервальных рядах динамики (
§ y — уровни ряда (y1, y2 ,...,yn), § n — число периодов (число уровней ряда). Моментные ряды динамики Уровни моментных рядов динамики характеризуют состояние изучаемого явления на определенные моменты времени. Каждый последующий уровень включает в себя полностью или частично предыдущий показатель. Так, например, число работников на 1 апреля 1999 г. полностью или частично включает число работников на 1 марта. Если сложить эти показатели, то получим повторный счет тех работников, которые работали в течение всего месяца. Полученная сумма экономического содержания не имеет, это расчетный показатель. В моментных рядах динамики с равными интервалами времени средний уровень ряда исчисляется по формулесредней хронологической :
§ y -уровни моментного ряда; § n -число моментов (уровней ряда); § n — 1 — число периодов времени (лет, кварталов, месяцев).
Индекс денежных показателей Индексация - это компенсация инфляционных потерь доходов и сбережений населения, а также реальной стоимости других денежных показателей, при помощи подвижной шкалы индексов инфляционного роста цен, которые корректируют величину текущей денежной оценки. Для индексации заработной платы и других денежных доходов чаще всего используется следующая формула:
Различают два основных вида индексации: 1) индексация на общегосударственном уровне при помощи законодательно установленных индексов инфляции (индексов роста потребительских цен (англ.consumer price index, CPI и др.); 2) индексация на локальном уровне ежегодных соглашений между работниками и работодателями предприятий, организаций и учреждений. Индексный метод Индексный метод анализа применяется для анализа функциональных мультипликативных связей двух видов: Индексация доходов Индексация доходов – это установленный законами и другими нормативно-правовыми актами механизм пересчета и изменения денежных доходов населения (зарплаты, пенсий, стипендий) с учетом динамики розничных цен для полной или частичной компенсации потерь в доходах в результате инфляции; одна из форм социальной защиты населения от инфляции. Индексация оказывает поддержку в предотвращении снижения реальной заработной платы или минимизировании степени снижения. Индексации подлежит не только начисляемая заработная плата, но и другие выплаты, которые причитаются работнику, т. е. он имеет право на индексацию сумм задержанной заработной платы в связи с их обесцениванием вследствие инфляции. Законодатель (орган исполнительной власти, орган местного самоуправления, работодатель) имеет право выбрать любые критерии для проведения индексации и предусмотреть любой порядок ее осуществления. Как правило, индексация осуществляется путем повышения тарифных ставок (должностных окладов). Величина увеличения, его повторяемость, минимальные и максимальные размеры определяются соответствующим органом государственной власти или работодателем. Повышение должностных окладов работников организаций, финансируемых из бюджета, обычно осуществляется раз в год (2-3 года) и охватывает всех без исключения работников указанных организаций. Размер повышения должностных окладов устанавливается в процентах к действующим окладам. Новые оклады используются до следующего повышения. Индексация заработной платы работников организаций, не получающих бюджетного финансирования, либо работодателей – физических лиц осуществляется по правилам, ими самими установленным.
Индикаторы систем Поверхностный взгляд на тексты индикаторов на исходном языке, например, MQL5, позволяет выявить две формы их задания: аналитическая (наиболее распространенная) и табличная (применяется к индикаторам, которые называют фильтрами, например, индикаторы Кравчука). Мы же будем использовать термин регрессия – общепринятый термин в математической статистике и эконометрике. Имея идею, что же мы хотим выделить из котировок, для формулирования регрессии (индикатора) необходимо задать: Перечень независимых переменных, по которым вычисляется индикатор; Коэффициенты при независимых переменных; Формулу вычисления индикатора, по которой будет вычисляться зависимая переменная. Если при построении мультивалютных индикаторов имеются сложности, то в регрессии таких ограничений нет. Имея эти три позиции, в дальнейшем следует подогнать регрессию к котировке. В отличие от трейдерских форумов в эконометрике слово «подгонка – fit, fitting» не является ругательным, а является стандартной процедурой, в ходе которой с помощью одного из многочисленных методов оценки вычисляется соответствие регрессии (индикатора) котировкам. Наиболее известным из методов оценки является метод наименьших квадратов (МНК). В результате оценки нас интересует два вопроса: Соответствие индикатора котировкам – величина остающейся ошибки; Стабильность вычисленных параметров регрессии в будущем. Ответы на эти вопросы даются в ходе диагностики индикаторов. Диагностика индикаторов Диагностика индикаторов (регрессий) разделена на три группы: Диагностика коэффициентов; Диагностика остатков; Диагностика стабильности. Каждая процедура проверки, описанная ниже, включает спецификацию нулевой гипотезы, которая является гипотезой при тесте. Результат теста состоит из выборки значений одной или более статистик и их присоединенных р-значений. Последние указывают на вероятность выполнения условия нулевой гипотезы, на которой построена тестовая статистика. Таким образом, малые р-значения приводят к отклонению нулевой гипотезы. Например, если р-значение лежит между 0.05 и 0.01, то нулевая гипотеза отклонена на пяти процентном уровне, но не на однопроцентном уровне. Следует учесть, что имеются различные предположения и результаты распределения, связанные с каждым тестом. Например, у некоторых из статистик есть точные, конечные тестовые распределения (обычно t или F-распределения). Другие являются большими выборками тестовой статистики с асимптотическими χ2 распределениями.
Индекс объема Основным видом несплошного наблюдения является выборочное наблюдение. Выборочные обследования массовых явлений проводятся во всех странах и областях жизни - в экономике, политике, бизнесе, науке, технике и т.д. Статистическая выборка - это несплошное наблюдение, которое предполагает формирование и исследование выборочной совокупности как уменьшенной копии генеральной совокупности. Генеральная совокупность - это полная (целостная) совокупность единиц, из которых выбирают единицы для исследования. Выборочная совокупность – это совокупность отобранных для исследования единиц генеральной совокупности. Выборочное наблюдение имеет следующие основные преимущества перед сплошным наблюдением: 1) экономия времени, а также материальных, технических и финансовых ресурсов на проведение наблюдения; 2) возможность более глубокого исследования небольшого количества единиц выборочной совокупности за счет экономии времени и ресурсов на обследование остальных единиц генеральной совокупности. По схеме отбора единиц совокупности различают следующие основные виды статистических выборок: простая повторная и бесповторная, механическая, типическая (районированная), серийная (гнездовая), многоступенчатая, многофазная, комбинированная. Простая повторная выборка - это выборка, в которой случайно отобранная и исследованная единица возвращается в генеральную совокупность для повторного обследования. Простая бесповторная выборка - это выборка, в которой каждая случайно отобранная единица не возвращается в генеральную совокупность. Механическая выборка - это выборка, которая всю генеральную совокупность механически разделяет на равные части в соответствии с выбранными признаками и в каждой такой части обследуется лишь одна единица. Например, исследуется определенное число единиц совокупности через определенный интервал в 5%, 10% и т.д. Типическая выборка - это выборка, в соответствии с которой всю генеральную совокупность делят на однородные группы (типы, районы) и из каждой такой группы обследуют определенное число единиц совокупности. Серийная выборка предполагает исследование не отдельных единиц совокупности, а их серий, гнезд. Многоступенчатая выборка – это выборка, в которой из генеральной совокупности на первой ступени выбираются увеличенные группы, на второй - более мелкие, и так, пока не будут отобраны все единицы, подлежащие наблюдению. Многофазная выборка предполагает последовательное расширение программы обследования отобранных единиц в каждой новой фазе (стадии). При этом на каждой новой фазе формируют выборочные совокупности уменьшенного объема из единиц, которые уже были обследованы на предыдущей фазе. Выборочные характеристики каждой фазы используют как дополнительную информацию на следующих фазах. Все это повышает точность многофазной выборки. Комбинированная выборка объединяет различные виды выборок. Для обеспечения достоверности статистической выборки рассчитывают следующие основные ее характеристики: 1) предельную ошибку полученных результатов; 2) границы доверительного интервала выборочной оценки; 3) минимально достаточный объем выборки. Доказано, что предельная ошибка составляет: 1) для повторной выборки:
2) для бесповторной выборки:
где N – количество единиц всей генеральной совокупности. Из приведенных формул видно, что бесповторная выборка обеспечивает более точные результаты, чем повторная, поскольку множитель (1-n/N) всегда меньше единицы, то есть он уменьшает величину ошибки бесповторной выборки. Поэтому на практике используют преимущественно бесповторную выборку. Величина предельной ошибки выборки зависит от таких факторов: вариации признака в генеральной
обратно пропорциональна. Поэтому, чтобы уменьшить ошибку выборки, например, в 2 раза, объем выборки должен возрасти в 4 раза..
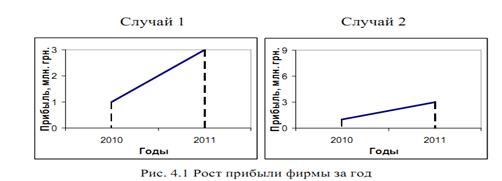
Абсолютная величина Статистика измеряет и выражает явления общественной жизни с помощью количественных категорий — статистических величин. Результаты статистического наблюдения получают прежде всего в форме абсолютных величин, которые служат основой для расчета и анализа статистических показателей на следующих этапах статистического исследования. Простые натуральные единицы измерения — это тонны, километры, штуки, литры, мили, дюймы и т. д. В простых натуральных единицах также измеряется объем статистической совокупности, т. е. число составляющих ее единиц, или объем отдельной ее части. Составные натуральные единицы измерения имеют расчетные показатели, получаемые как произведение двух или нескольких показателей, имеющих простые единицы измерения. Например, учет затрат труда на предприятиях выражается в отработанных человеко-днях (число работников предприятия умножается на количество отработанных за период дней) или человеко-часах (число работников предприятия умножается на среднюю продолжительность одного рабочего дня и на количество рабочих дней в периоде); грузооборот транспорта выражается в тонно-километрах (масса перевезенного груза умножается на расстояние перевозки) и т. д. Условно-натуральные единицы измерения широко используют в анализе производственной деятельности, когда требуется найти итоговое значение однотипных показателей, которые напрямую несопоставимы, но характеризуют одни и те же свойства объекта. Натуральные единицы пересчитываются в условно-натуральные путем выражения разновидностей явления в единицах какого-либо эталона. Относительные величины Наряду с абсолютными величинами в экономическом анализе и экономической статистике используются также различные относительные величины. Относительные величины представляют собой различные коэффициенты или проценты. Основные виды графиков Статистические графики - это наглядные изображения статистических данных при помощи геометрических образов. Единственное преимущество графиков по сравнению с текстом и статистическими показателями - это наглядность. Ради наглядности и строятся графики. Каждый график должен иметь название над графиком или под ним. В названии указываются: наименование изображенных показателей, их единицы измерения, объект, территория и период времени, к которым относятся показатели. Графики часто зависят от масштаба изображения данных. Поэтому для окончательных выводов нужно всегда проверять масштаб графика. Например, на рис. 4.1 изображены одни и те же данные, но в разном масштабе. На первый взгляд рост прибыли фирмы в случае 1 больше, чем в случае 2. Однако на рис. 4.1 изображены одни и те же данные, но в разном масштабе соотношения абсциссы к ординате.
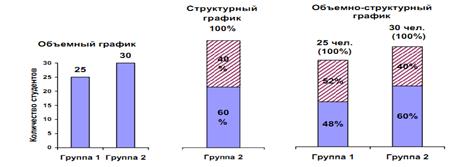
Графики делятся на основные и специальные. Основные – это наиболее распространенные графики. Специальные - это графики, которые используют для специальных целей. Основные графики подразделяют на три вида: столбиковые, круговые, кривые линии. Столбиковые графики отображают статистические данные в виде прямоугольников (столбиков) одинаковой ширины. Различают три основных вида столбиковых графиков: объемные, структурные и объемно-структурные. В объемных графиках высота каждого столбика пропорциональна величине изображаемых явлений. Цифры, как правило, записывают внутри колонок или над ними. В структурных графиках высота каждого столбика одинакова и составляет 100% или 1. Столбик делят на части пропорционально структуре изображаемого явления. Объемно-структурный график объединяет объемный и структурный график. Например, численность двух академических групп студентов и их структуру по полу можно охарактеризовать столбовыми графиками, которые изображены на рис. 4.2.
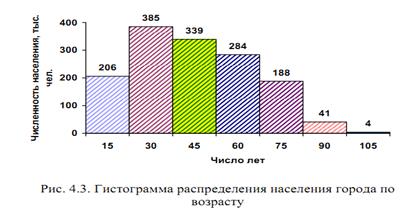
Разновидностями столбиковых графиков является гистограмма распределения и ленточный график. Гистограмма распределения - это столбиковой график, на оси абсцисс которого откладывают равные или неравные интервалы распределения любого явления, а на оси ординат - высоту столбиков, которая пропорциональна количеству единиц совокупности в соответствующем интервале или их частоте в процентах к общему итогу (рис.4.3).
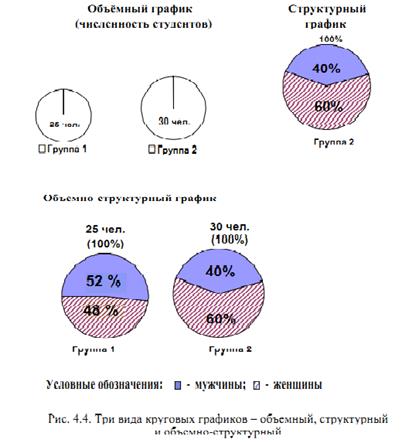
Если столбики расположены горизонтально, график называется ленточным. Длина строки в ленточном графике пропорциональна величине показателя. Методика построения ленточных графиков с горизонтальной масштабной шкалой аналогична построению столбиковых графиков с вертикальной шкалой. Круговые графики отображают статистические данные в виде площади круга. Различают три основных вида круговых графиков: объемные, структурные (секторные) и объемно-структурные. В объемных графиках площадь круга пропорциональна величине изображаемого показателя. В структурных графиках площадь круга принимают равной 100%, из расчета, что 1% составляет угол в 3,6 °. Исходя из этого, круг делят на секторы пропорционально структуре изображаемого явления. Объемно-структурный график объединяет объемный и структурный график. Например, данные двух академических групп студентов, которые изображены на рис. 4.2. столбиками, можно охарактеризовать круговыми графиками (рис. 4.4). На практике чаще всего используют структурные (секторные) круговые графики. Кривые - это графики в форме различных кривых, которые строят в системе прямоугольных координат. Различают три основных вида кривых: графики динамики, зависимости и распределения.
Графики динамики показывают изменения статистических данных во времени. Например, изменение численности легковых автомобилей в городе (рис. 4.5).
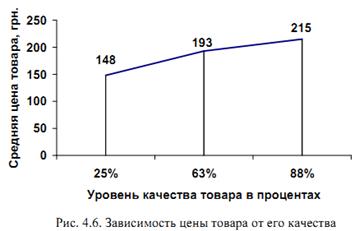
Графики зависимости - характеризуют зависимость одних явлений от других. Например, зависимость цены товара от его качества по данным табл. 4.2. (рис. 4.6).
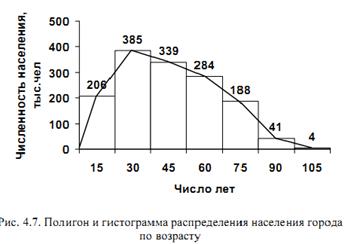
Для построения графиков с показателями, которые охватывают интервалы, используют середины интервалов. Например, на рис. 4.6 для средних цен взяты середины интервалов уровня качества товара: 25%, 63%, 88%. График показывает, что цена товара зависит от его качества. Однако эта зависимость не прямо пропорциональная. Графики распределения показывают распределение статистической совокупности по определенным признакам. Примером таких графиков является полигон распределения. Полигон распределения - это кривая линия, для построения которой на оси абсцисс откладывают значения любого признака, а на оси ординат - распределение по этому признаку количества единиц совокупности или их частот в процентах к общему итогу. Полигон распределения можно объединять с гистограммой. Общий график полигона и гистограммы распределения по данным рис. 4.3. приведен на рис. 4.7.
Статистическая информация используется во всех сферах деятельности для самых различных специальных целей. Поэтому существует много специальных графиков. Среди них чаще всего применяются картограммы, картодиаграммы, фигурные графики, радиальные диаграммы, график В.Е. Варзара и др. Картограмма - это географическая карта, на которой исследуется территориальное распределение статистической совокупности по определенному признаку путем нанесения ее значений точками, штриховкой, закрашиванием разными цветами и т.п. Например, при помощи картограмм можно изобразить распределение по регионам всех видов ресурсов, продукции, инвестиций, урожайности, плотности населения, уровня его занятости и т.д. Картодиаграмма - это географическая карта, в разных частях которой построены локальные графики (диаграммы) в форме столбиков, кругов и т.д. Фигурные графики - это различные графические фигуры определенного масштаба, напоминающие изображаемые явления. Например, для показателя производства автомобилей это может быть изображение автомобиля разной величины с соответствующей цифрой их выпуска. Радиальные диаграммы - это круг с масштабом временных или иных интервалов, на радиусах которого отображают изменение величины статистических показателей. Радиальные диаграммы применяют для анализа колебаний показателей во времени. График В.Е.Варзара показывает размеры сразу трех показателей, взаимосвязанных между собой так, что произведение первых двух равно третьему: х1умножить на х2 ═ у. График В.Е.Варзара - это прямоугольник, основанием которого является один показатель (х1), высотой - второй (х2), а их произведение - площадь прямоугольника - третий (у).
История статистики Профессиональная подготовка в любом виде деятельности невозможна без знания профессиональной истории (истории профессиональных знаний, умений и практических навыков). Только знание профессиональной истории позволяет учесть закономерности и тенденции изучаемых процессов, избежать уже случившихся в истории ошибок. Часто история того или иного вопроса является ключом для решения самых сложных проблем. Статистика - одна из древнейших и важнейших областей человеческой деятельности. Еще в Древнем Египте, более 5 тысяч лет назад, проводились статистические переписи населения, вычислялись индексы цен и другие статистические показатели. В 2112-2094 гг. до н.э. в Древнем Шумере (Передняя Азия) в «Законах царя Ур-Намму» содержатся не известные до сих пор данные о древнейших деньгах - «шекелях» (8,4 г. серебра) и «минах» (505г. серебра) и об учете в этих деньгах всех налогов и платежей. С этого времени статистический учет в деньгах распространился по всему миру. В 1165 г. до н. э. писцы фараона Рамсеса III наладили статистический учет огромного числа существовавших в то время товаров, драгоценных металлов, денег, оружия, зерна, скота, имущества, земли. В это время возникли старейшие статистические учреждения по учету всех богатств и ресурсов Древнего Египта (специальные «дома» и «палаты» как общегосударственные службы фараона). В трудах выдающегося древнегреческого ученого Аристотеля (Aristotle; 384-322г.г. до н. э.) можно встретить такие понятия, как "число", "система" и "фактор", которые играют исключительно важную роль в современной статистике. В Древнем Китае, Вавилоне, Греции зародилась финансовая статистика. В Древнем Вавилоне уже в VI веке до н.э. существовали банки Эгиби, Иддин-Мардука и других богачей. В Афинах в VI веке до н.э. возникли конторы трапезитов-банкиров Греции, которые систематически регистрировали все финансовые операции по платежам и хранению денег. Во ІІ веке в Китае появилась бумага, а в VIII веке – старейшие бумажные деньги. Постепенно стали формироваться статистические методы. Стали использоваться индексы и балансы. Балансовый метод зародился еще в Древнем Шумере. Однако лишь в 1494 году «отец» современного бухгалтерского учета итальянский ученый Лука Пачоли (L.Pacioli; ок. 1445-1514) использовал балансовый метод для постоянного учета движения материальных ценностей. Как вполне самостоятельная научная дисциплина статистика сформировалась значительно позже. Лишь в 1675г. был издан учебник по статистике государств немецкого профессора Германа Конринга, а в 1747г. немецкий ученый Г.Ахенвалль ввел в научный оборот термин "статистика". В 18 - 19 вв. возникли статистические учреждения многих стран: Великобритании – в 1700г. (Парламентская статистика; публикация «Синих книг»), Швеции – 1756г. («Табельная комиссия»), Дании – 1783г. («Табельная комиссия»), Франции – 1789г. (статистическое бюро в министерстве финансов), Германии (Пруссии) – 1805г., России – 1802г. (Центральное статистическое бюро), Австрии – 1810г. («Тайное статистическое бюро»), Нидерландов – 1826г., Бельгии – 1831г., Швейцарии – 1849г., Испании – 1856г., Италии (после объединения итальянских государств) – 1861г., США – 1866г. (Статистическое бюро Министерства торговли). В Украине статистические данные известны еще со времени возникновения Херсонеса Таврического в Крыму в 528 г. до н. э. В Киевской Руси проводились статистические переписи населения, велся статистический учет денежных средств, земли и имущества. В 1835 г. были учреждены губернские статистические комитеты. В 1861 году было отменено крепостное право на крестьян. Статистика приобрела большую популярность в «образованном обществе». Множество лю
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 499; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.5.216 (0.016 с.) |



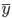 ) исчисляется по формуле средней арифметической простой:
) исчисляется по формуле средней арифметической простой: