Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В зависимости от насыщенности данными выделяют простые и сложные таблицы. Последние, в свою очередь, делятся на групповые и комбинационные.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В простой таблице дается распределение, ряды распределения одного учетного признака (имеется одно сказуемое). Часто это распределение приводится вместе с одной или несколькими количественными характеристиками этого распределения. Как правило, эти характеристики приводятся в виде относительных величин (интенсивных и экстенсивных коэффициентов, коэффициентов соотношения и т.п.). Таблица 2 Макет простой таблицы (таблица сопряженности)
В сложной таблице имеются несколько сказуемых. В групповой таблице дается распределение единиц наблюдения по двум и более признакам, не связанным между собой. Наряду с абсолютными показателями и таблице могут быть любые производные величины. В том случае, когда в таблице приводятся показатели структуры, рекомендуется указывать графу или строку, от которой идет отсчет частей (100%). Таблица 3
Простые и групповые статистические таблицы дают возможность проводить, как правило, только ориентировочный, предварительный анализ. В таких таблицах невозможно проследить взаимосвязи нескольких отдельных факторов. Более того, увиденные в этих таблицах тенденции могут быть ошибочно приписаны одному группировочному признаку. Для изучения сравнительной роли различных факторов используется система комбинационных группировок, выполняемая с помощью комбинационных таблиц. В таких таблицах, как правило, оценивается распределение взаимосвязанных признаков. Таблица 4
Правильно построенная таблица является самодостаточной, то есть представленные в ней данные понятны без дополнительного обращения к тексту.
Графические изображения
Графические изображения - это условные изображения числовых величин и их соотношений в виде геометрических образов. Графические изображения, использующиеся для более наглядного отображения статистических данных, называются диаграммами. В некоторых случаях диаграммы позволяют проводить более точный анализ, поскольку при их помощи легче уяснить закономерности развития, распределения и размещения явлений.
Часто разного рода ошибки и неточности выявляются именно при применении диаграмм. Весь вопрос в том, как найти правильное графическое решение для анализа данных. При построении статистической диаграммы необходимо правильно выбрать графический образ диаграммы и ее экспликацию. Экспликация включает словесные пояснения к помещенным на графике геометрическим фигурам и вспомогательные изобразительные средства (системы координат, шкалы, масштабные сетки, наименование графика, единиц измерения, числовых данных и отдельных деталей). Целесообразно придерживаться следующих правил построения диаграмм: 1) Общая структура диаграммы должна предполагать чтение слева направо. 2) Следует избегать попыток изображения линейных величин с помощью площадей и объемов, как не соответствующих сути показателей. Кроме того, следует помнить, что из-за обмана зрения могут возникать ошибки сравнительного восприятия отображаемых величин. 3) Вертикальную шкалу для кривой независимо от ее назначения следует выбрать так, чтобы на диаграмме оказалась нулевая отметка. Иногда это невозможно, например, из-за больших значений показателей. В этом случае отсчет шкалы целесообразно делать по возможности от круглого числа, либо от уровня имеющего какое-либо смысловое значение (стандарт, среднее и т.п.). 4) Для кривых, имеющих шкалу, изображающую проценты, промилле и т. п., каким-то образом выделяются соответственно 100, 1000, 10000 и т.д. Целесообразно выделять величины, обозначающие норму, стандарт или средний уровень показателей. 5) Когда шкалы относятся к датам, лучше не выделять первые и последние ординаты, т.к. подобные диаграммы, как правило, не отражают начало и конец времени. 6) Для кривых, характеризующих группы наблюдений, рекомендуется по возможности ясно указывать на диаграмме все кривые, представляющие отдельные наблюдения. 7) Горизонтальную шкалу для кривых следует читать, как правило, слева направо, а вертикальную — снизу вверх. Если отображаемые данные резко отличаются друг от друга по своей величине, рекомендуется делать разрыв масштабной шкалы. Этот же прием применяется, если нет данных за какой-либо отрезок анализируемого периода. При этом необходимо соблюдение двух условий. Во-первых, данные должны быть однородны, во-вторых, разрыв должен быть обозначен и на построенной кривой. В том случае, когда вырезки делать нецелесообразно (необходим анализ всего числового ряда без промежутков), рекомендуется использовать логарифмические шкалы.
8) Цифры на шкалах следует располагать слева и снизу вдоль соответствующих осей. Если цифровые данные не попали на диаграмму, желательно привести данные в таблице, сопровождающей диаграмму. 9) Желательно включать в диаграмму цифровые данные или используемые формулы. 10) Наименования следует давать возможно яснее и полнее. Если это требуется, необходимо вводить подзаголовки и пояснения. 11) При использовании условных обозначений необходимо давать пояснения к ним. 12) Наименования графических изображений в книгах, журналах обычно указывают снизу от рисунка. Названия таблиц — вверху. В диаграммах, не предусмотренных для печати, например настенных диаграммах, слайдах, целесообразно писать заголовки сверху. 13) При построении линейной диаграммы в двухосной системе координат соотношение горизонтальной и вертикальной осей по длине целесообразно выбирать на основе принципа золотого сечения. Это такое сечение, при котором отношение целого отрезка к большей его части равняется отношению большей части к меньшей. В наиболее обобщенном виде это соотношение равно 3 к 2. 14) При использовании в нескольких последовательно расположенных диаграммах одних и тех же учетных признаков, применяются обязательно одни и те же условные обозначения для этих признаков. При построении секторной диаграммы начало отсчета производится от верхней точки («12 часов») и по ходу часовой стрелки. Следует помнить, что секторная диаграмма не допускает разбиения на большое число секторов (частей). Не рекомендуется использовать эту диаграмму для отображения более 5—7 показателей. Если такая необходимость существует, то нужно использовать другой тип диаграмм. Целесообразно откладывать числовые значения признака от большего к меньшему. Если этот порядок противоречит логической последовательности данных, то он может быть нарушен. Основные типы диаграмм
В настоящее время, благодаря широкому использованию персональных компьютеров и пакетов специализированных прикладных программ, фактически не существует никаких ограничений, которые ранее диктовались трудоемкостью создания тех или иных типов диаграмм. Фигурные диаграммы наиболее целесообразно применять при демонстрации каких-либо данных для широкой аудитории, не имеющей специальной подготовки (санитарно-просветительная работа, массовая агитация и т. п.) (рис. 1).
Рисунок 1. Патологическая пораженность (количество заболеваний) на 1000 студентов КрасГМУ по данным медицинского осмотра в 2009 году
Рисунок 2. Динамика численности населения России с 1897 г. по 2004 г.
Рисунок 3. Динамика заболеваемости взрослого населения Красноярского края в 2001-2006 гг.
Особым типом столбиковых диаграмм, который используется для иллюстрации плана, графика работ по какому-либо проекту является ленточная диаграмма (диагра́мма Га́нта). При этом, каждый раздел плана изображается в виде столбика, пропорционального по размерам его длительности. Для отражения изменений экстенсивных показателей более целесообразно использовать внутристолбиковые диаграммы (рис. 4).
Рисунок 5. Структура причин смерти в Красноярском крае в 2006 г.
Для отображения сезонных и циклических явлений оптимальным вариантом является радиальная диаграмма (рис. 6).
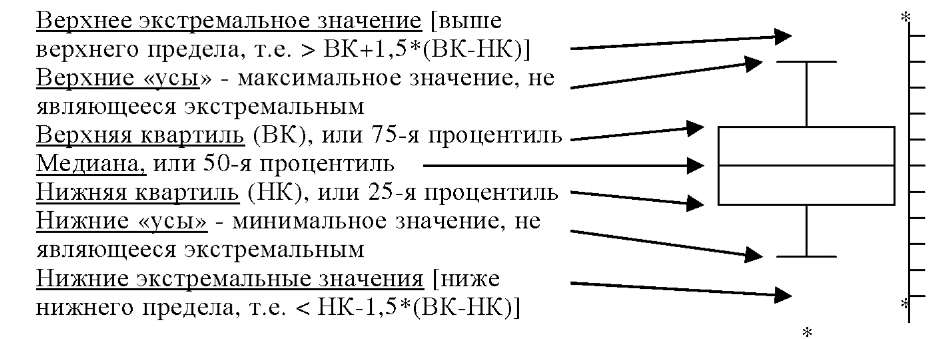
Главным критерием выбора той или иной диаграммы для отображения статистических показателей является наглядность и удобство анализа результатов. Например: если анализируется сравнительная заболеваемость мужчин и женщин, то более целесообразно представить попарно сгруппированные показатели мужчин и женщин. Картограмма – это географическая карта или ее схема, на которой приведены определенные статистические данные (с помощью цветовой гаммы или различной штриховки территорий). Картодиаграмма – это сочетание географической карты или ее схемы с различными диаграммами, представляющими статистические данные, относящиеся к определенным территориям. Коробчатую диаграмму называют «коробкой с усами», «ящиком с усами», а по-английски boxplot. Данный тип визуализации данных одновременно изображает пять величин, характеризующих вариационный ряд: минимальное значение, первую квартиль (или 25 процентиль), медиану, третью квартиль (75 процентиль), максимальное значение. Таким образом, польза коробчатой диаграммы заключается в том, что на ней не только представлены основные характеристики распределения, но и доступен для оценки размах вариации, и ее асимметрия. Коробчатые диаграммы очень компактны, с их помощью удобно сравнивать характер распределения в нескольких рядах.
Коробчатая диаграмма может быть как вертикальной, так и горизонтальной. Основой ее является прямоугольник, нижняя (левая, если график горизонтальный) сторона – это нижний квартиль (Q1), а верхняя (правая) – верхний квартиль (Q3). Высота (длина) прямоугольника, таким образом, равна межквартильному интервалу (IQR). Черта поперек прямоугольника – это медиана распределения (рис. 7).
Рисунок 7. Особенности коробчатой диаграммы
Гистограмма характеризует распределение количественного признака, применяется для графического изображения интервальных рядов распределения. Внешне она представляет собой многоугольник, построенный с помощью смежных четырехугольников. Ширина основания каждого четырехугольника соответствует границам группы вариант. Высота столбика определяется частотой группы. На шкале «Х» в выбранном масштабе откладываются интервалы значений переменной. Интервалы не должны перекрывать друг друга или иметь пропуски возможных значений переменной. На оси «Х» указываются центр или границы каждого интервала. Ось «Y» служит шкалой плотности, т.е. на ней откладываются абсолютные (число наблюдений) или относительные значения (доля, процент наблюдений) на единицу шага значения переменной. В простейшем варианте (при условии одинаковой ширины интервалов на оси Х) шаг целого интервала принимается за 1. Общее число (или долю) наблюдений характеризует не высота столбца, а его площадь. Высота столбца отражает плотность распределения признака в определенном интервале его значений. Площадь всех столбцов гистограммы должна равняться 100% (при относительной шкале плотности) или общей сумме наблюдений (при абсолютной шкале плотности). Одновременное изображение на гистограмме кривой нормального распределения позволяет зрительно оценить, насколько эмпирическое распределение отличается от нормального (рис. 8).
Рисунок 8. Пример гистограммы с кривой нормального распределения: гистограмма возраста обследованных лиц
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 419; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.105.46 (0.011 с.) |





 Рисунок 6. Зависимость расстояния проживания от реки Енисей и числа посещений по поводу болезней лор-органов и органов дыхания на 1000 детей г. Красноярска (в 2005 году)
Рисунок 6. Зависимость расстояния проживания от реки Енисей и числа посещений по поводу болезней лор-органов и органов дыхания на 1000 детей г. Красноярска (в 2005 году)