
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистические моменты плоской фигурыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Статистические моменты плоской фигуры
Координаты центра масс
Координаты плоской фигуры
Моменты инерции плоской фигуры
Моментом инерции материальной точки массы Моменты инерции плоской фигуры
Момент инерции плоской фигуры
Тройной интеграл. Схема получения тройного интеграла. Схема получения тройного интеграла 1) Разбиваем область 2) Объем «элементарной области» 3) Возьмем произвольную точку 4) Находим 5) Составляем интегральную сумму
6) Обозначим через
Предел интегральной суммы, когда число «элементарных областей» неограниченно возрастает, а длина наибольшего диаметра стремится к нулю, называется тройным интегралом от
Таким образом, тройным интегралом от
7. Основные свойства тройного интеграла (хотя бы 4 свойства). Формула вычисления тройного интеграла в декартовой системе координат. Свойства: 1.
2. 3. Если область
4. Если в области
5. Если в области
Тогда тройной интеграл в декартовых координатах вычисляется по следующей формуле:
Замена переменной в тройном интеграле. Вычисление тройного интеграла в цилиндрических координатах. При вычислении тройного интеграла, как и для двойного, часто применяется метод подстановки, т.е. совершается преобразование переменных. Пусть совершается подстановка
то справедлива формула замены переменной в тройном интеграле:
(1.9) Здесь
|
||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 1026; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.99.39 (0.008 с.) |

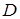 относительно осей
относительно осей 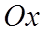 и
и  могут быть вычислены по формулам:
могут быть вычислены по формулам: ;
; .
.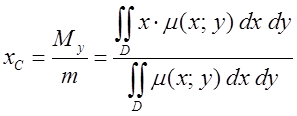 ;
; .
. относительно оси
относительно оси  называется произведение массы
называется произведение массы 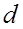 точки до оси, т.е.
точки до оси, т.е.  .
. относительно осей
относительно осей  и
и  могут быть вычислены по формулам:
могут быть вычислены по формулам: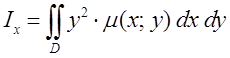 ;
;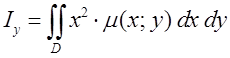 .
.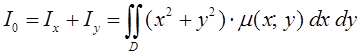 .
. на
на  «элементарных областей»
«элементарных областей» 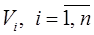 .
. обозначим
обозначим  , а диаметр (наибольшее расстояние между двумя точками области) – через
, а диаметр (наибольшее расстояние между двумя точками области) – через  .
.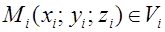 .
. .
. .
. длину наибольшего из диаметров «элементарных областей», т.е.
длину наибольшего из диаметров «элементарных областей», т.е.  ,
,  . Найдем предел интегральной суммы, когда
. Найдем предел интегральной суммы, когда 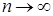 так, что
так, что  .
. .
. на замкнутой областью
на замкнутой областью  .
. по замкнутой областью
по замкнутой областью  , когда число «элементарных областей» неограниченно возрастает, а длина наибольшего диаметра стремится к нулю:
, когда число «элементарных областей» неограниченно возрастает, а длина наибольшего диаметра стремится к нулю: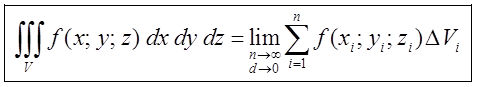 . (1.7)
. (1.7) - интегрируемая функция в области
- интегрируемая функция в области  ,
,  и
и 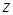 - переменные интегрирования;
- переменные интегрирования; или
или  - элемент объема.
- элемент объема. , где
, где  .
.
 и
и 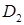 такие, что
такие, что  , а пересечение
, а пересечение 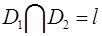 , где
, где  - линия, разделяющая
- линия, разделяющая 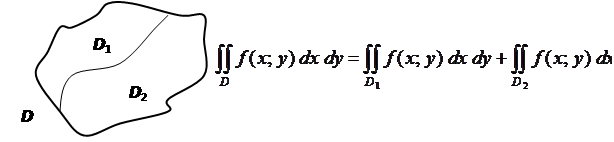
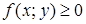 , то и
, то и .
. функции
функции  и
и  удовлетворяют неравенству
удовлетворяют неравенству  , то и
, то и .
. . (1.8)
. (1.8) ,
,  и
и  . Если эти функции имеют в некоторой области
. Если эти функции имеют в некоторой области 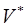 пространства
пространства 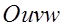 непрерывные частные производные и отличный от нуля определитель
непрерывные частные производные и отличный от нуля определитель ,
,
 - определитель Якоби, или якобиан преобразования (примем без доказательства)
- определитель Якоби, или якобиан преобразования (примем без доказательства)


