Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Способ перемены плоскостей проекцийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Способ совмещения.
Рисунок 5
Рисунок 6
Способ перемены плоскостей проекций Способ перемены плоскостей проекций состоит в том, что основную систему плоскостей проекций, в которой есть проекции оригинала, заменяют новой системой двух взаимно перпендикулярных плоскостей, причем положение оригинала остается прежним.
ПРИМЕР 1. Задача преобразования- определить длину отрезка. Применение системы П1П4 на рисунке 7. На комплексном чертеже плоскость П2 заменена плоскостьюП4. Причем новая плоскость должна быть параллельна отрезку АВ, тогда новая ось S14 должна расположится параллельно горизонтальной проекции A1B1 (проводится на любом расстоянии от проекции A1 B1). Проецируется точки А и В на плоскость π4, получают проекции A4 и В4. Соединяют эти точки прямой. Новая проекция А4В4 отрезка АВ будет равна его действительной величине. Координаты z точек А и В остаются неизменными.
ПРИМЕР 2. Задача преобразования определить длину отрезка. Применение системы П2П4 в рисунке 8. В данном случае плоскость П1 заменена плоскостью П4. Новая ось S14 параллельна фронтальной проекции А2В2, и новая проекция А4B4 в системе П2 П4 будет равна длине отрезка АВ. Координаты у точек А и В остаются неизменными.
Рисунок 7
Рисунок 8
ПРИМЕР 3. Задача преобразования определить натуральный вид треугольника рисунке в рассматриваемом случае может быть применена только система П1П4. Плоскость заданного треугольника перпендикулярна плоскости П1,поэтому плоскость П2 можно заменить лишь на плоскость П4 так, чтобы она была параллельна плоскости треугольника, т.е. плоскости @ Новая ось S14 располагается параллельно проекции A1B1C1 треугольника ABC. На проведенных из точек A1B1C1 линиях связи, пользуясь координатами точек ABC находят новую проекцию А4В4С4 представляет натуральный вид треугольника ABC, по которому можно определить его площадь, стороны и углы.
Сечение геометрических тел плоскостями. Сечение призмы плоскостью. Даны три проекции прямой треугольной призмы и фронтальная проекция b2 фронтально -проецирующей плоскости b, пересекающие призму на рисунке 10. Требуется построить проекции линии контура фигуры сечения, найти натуральною величину фигуры сечения; построить развертку поверхности усеченной призмы; построить стандартную изометрическую проекцию усечённой призмы. Основание призмы расположено в плоскости П1, поэтому ребра и грани призмы перпендикулярны плоскости П2. Профильная проекция D3E3F3 строится обычно, как третья по двум, при этом заметим, что сторона EF фигуры сечения закрыта двумя боковыми гранями призмы поэтому ее проекция E3F3 изобразится штриховой линией. Натуральную величину фигуры сечения найдём способом перемены плоскостей проекций. Вводим новую плоскость П4 так, чтобы она была параллельна фронтально проецирующей плоскости b. Проводят новую ось проекции S24 параллельно проекции b2 секущей плоскости b. На новой плоскости П4 строят новую проекцию D4Е4F4 фигуры сечения, она будет равна натуральной величине фигуры сечения, она будет равна натуральной величине фигуры сечения.
Взаимное пересечения поверхностей. Пересечение многогранников. Рекомендации к выполнению графических работ. Примеры графических работ №3 и №4 приведены ниже.
Рисунок 20
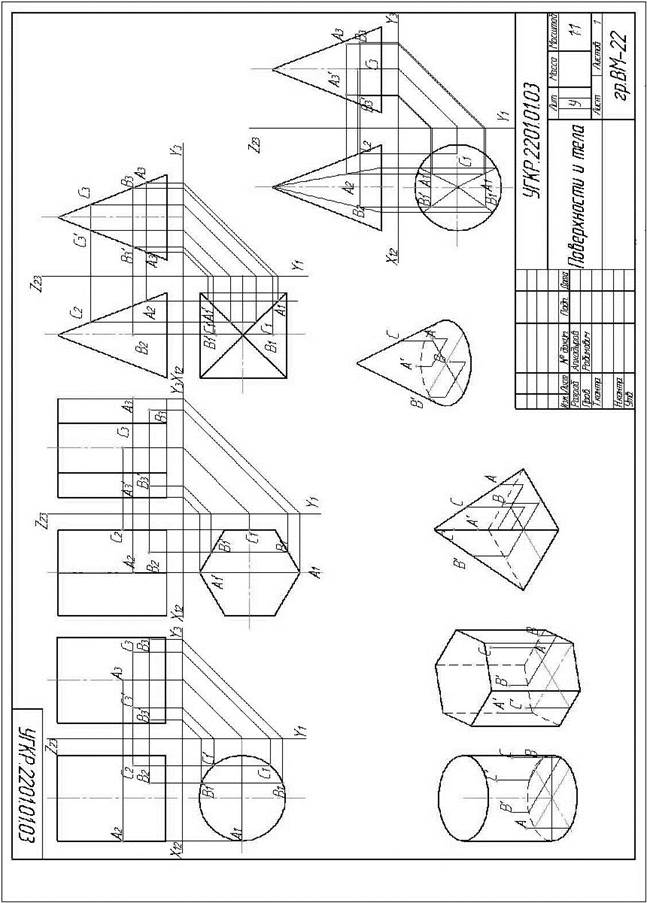
ГРАФИЧЕСКАЯ РАБОТА №5 МОДЕЛИ – КОМПЛЕКСНЫЕ ЧЕРТЕЖИ МОДЕЛЕЙ И ИХ АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ Цели графической работы №5 1.1 Учебные: - развитие умений по выполнению графических изображений; - развитие умений по построению комплексного чертежа моделей; - закрепление знаний по нанесению размеров; - закрепление знаний по выполнению аксонометрических проекций; - закрепление знаний по выполнению основной надписи. 1.2 Развивающие: - осознание расположения основных видов: - развитие пространственного мышления. 1.3 Воспитательные: - развитие чувства ответственности; - осознание необходимости завершения начатого дня.
Студент должен: уметь: - строить по двум проекциям третью проекцию модели; - вычерчивать аксонометрические проекции модели; - строить комплексные чертежи моделей по натурным образцам и по аксонометрическому изображению.
2. Рекомендации к выполнению графической работы № 5 Графическая работа выполняется на формате A3. 2.1. Содержание: - Выполнить комплексные чертежи 4-х моделей. - Нанести размеры. - Выполнить аксонометрические проекции данных моделей (две модели выполнить в прямоугольной диметрии, две — в прямоугольной изометрии).
2.2. Последовательность выполнения графической работы: - Произвести рациональную компоновку изображений. - Построить две данные проекции первой модели. - По двум данным проекциям модели построить третью. - Нанести размеры. - Выполнить аксонометрическую проекцию модели. - В последовательности, указанной выше, выполнить комплексные чертежи и аксонометрические проекции остальных трех моделей. Рисунок 1
Способ совмещения.
Рисунок 5
Рисунок 6
Способ перемены плоскостей проекций Способ перемены плоскостей проекций состоит в том, что основную систему плоскостей проекций, в которой есть проекции оригинала, заменяют новой системой двух взаимно перпендикулярных плоскостей, причем положение оригинала остается прежним.
ПРИМЕР 1. Задача преобразования- определить длину отрезка. Применение системы П1П4 на рисунке 7. На комплексном чертеже плоскость П2 заменена плоскостьюП4. Причем новая плоскость должна быть параллельна отрезку АВ, тогда новая ось S14 должна расположится параллельно горизонтальной проекции A1B1 (проводится на любом расстоянии от проекции A1 B1). Проецируется точки А и В на плоскость π4, получают проекции A4 и В4. Соединяют эти точки прямой. Новая проекция А4В4 отрезка АВ будет равна его действительной величине. Координаты z точек А и В остаются неизменными.
ПРИМЕР 2. Задача преобразования определить длину отрезка. Применение системы П2П4 в рисунке 8. В данном случае плоскость П1 заменена плоскостью П4. Новая ось S14 параллельна фронтальной проекции А2В2, и новая проекция А4B4 в системе П2 П4 будет равна длине отрезка АВ. Координаты у точек А и В остаются неизменными.
Рисунок 7
Рисунок 8
ПРИМЕР 3. Задача преобразования определить натуральный вид треугольника рисунке в рассматриваемом случае может быть применена только система П1П4. Плоскость заданного треугольника перпендикулярна плоскости П1,поэтому плоскость П2 можно заменить лишь на плоскость П4 так, чтобы она была параллельна плоскости треугольника, т.е. плоскости @ Новая ось S14 располагается параллельно проекции A1B1C1 треугольника ABC. На проведенных из точек A1B1C1 линиях связи, пользуясь координатами точек ABC находят новую проекцию А4В4С4 представляет натуральный вид треугольника ABC, по которому можно определить его площадь, стороны и углы.
|
||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1156; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.011 с.) |

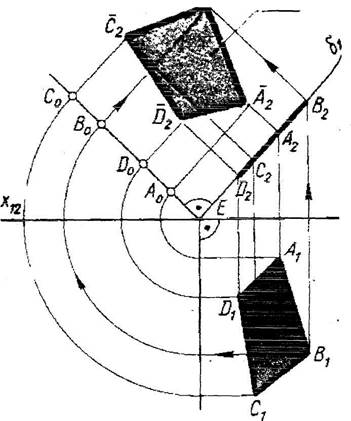
 Способ совмещения состоит в том, что плоскость, заданную следами, вращают вокруг одного из следов этой плоскости до совмещения с соответствующей плоскостью проекций. Тогда все линии и фигуры, лежащие в заданной плоскости, изобразятся на соответствующих.плоскостях проекций без искажения. Совмещение фронтально проецирующей плоскости b с расположенным в ней четырехугольником с плоскостью проекций П2 на рисунке 5. Совмещение фронтально проецирующей плоскости и с расположенным в ней четырехугольником с плоскостью проекций П2 на рисунке 6.
Способ совмещения состоит в том, что плоскость, заданную следами, вращают вокруг одного из следов этой плоскости до совмещения с соответствующей плоскостью проекций. Тогда все линии и фигуры, лежащие в заданной плоскости, изобразятся на соответствующих.плоскостях проекций без искажения. Совмещение фронтально проецирующей плоскости b с расположенным в ней четырехугольником с плоскостью проекций П2 на рисунке 5. Совмещение фронтально проецирующей плоскости и с расположенным в ней четырехугольником с плоскостью проекций П2 на рисунке 6.