Способ вращения. Способ плоскопараллельного переноса

Сущность метода вращения заключается в том, что при неизменном положении основных плоскостей проекции изменяется положение заданных гео­метрических объектов относительно плоскостей проекций путем их вращения вокруг некоторой оси до тех пор, пока зги объекты не займут частное положе­ние в исходной системе плоскостей.

В качестве осей вращения удобнее всего выбирать проецирующие прямые или прямые уровня. Тогда точки геометрических объектов будут вращать­ся в плоскостях, параллельных или перпендикулярных заданным плоскостям проекций. При повороте какого-либо геометрического объекта радиус поворота для каждой его точки - свой, а угол поворота для всех точек - одинаков. На комплексном чертеже при использовании метода вращения принято показывать положение оси вращения.

Как показано на рис. 38, при вращении вокруг горизонтально-проецирующей прямой i горизонтальная проекция A₁ точки А перемещается по окружности, а фронтальная, А₂, - по прямой, которая представляет собой проекцию окружности той плоскости, в которой вращается точка А.

 

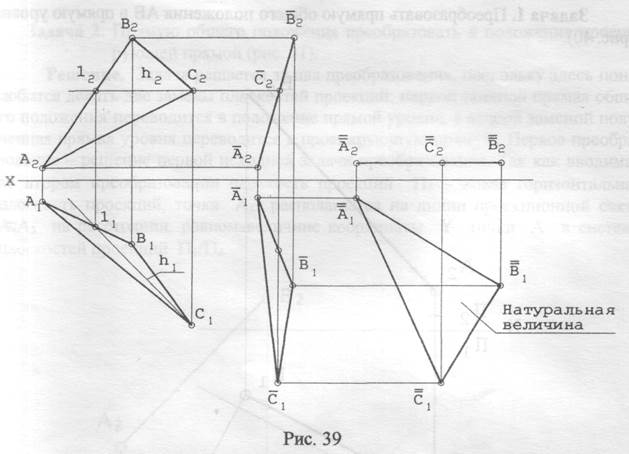
Заметим, что проекции точек на фронтальной плоскости проекций находятся на прямых, перпендикулярных исходным линиям связи. Используя это свойство, можно не задаваться изображением оси вращения и не устанавливать величину радиуса вращения. Тогда получаем метод плоскопараллельного пе­ремещения как частный случай метода вращения.

Применение способа плоскопараллельного переноса рассмотрим, решив следующую задачу.

Задача. Определить натуральную величину треугольника АВС (рис. 39).

Решение. Треугольник АВС следует расположить так, чтобы горизонтальная проекция горизонтали плоскости треугольника оказалась перпендику­лярной оси X. Поскольку горизонталь плоскости треугольника после такого преобразования станет фронтально-проецирующей прямой, а все горизонтали плоскости - параллельны, после такого преобразования плоскость треугольни­ка АВС станет фронтально-проецирующей плоскостью. Суть следующего преобразования - сделать плоскость ∆АВС параллельно горизонтальной плос­кости проекций. Для этого линию А₂⁼В₂⁼ нужно расположить параллельно оси X. Тогда ∆ А₁⁼В₁⁼С₁⁼ станет представлять натуральную величину ∆АВС.

 

13. Четыре исходных задачи преобразования чертежа

В подавляющем большинстве метрических задач участвуют прямые и плоскости. Если будет известно заранее, какие построения необходимо выполнить, чтобы прямая (или плоскость) общего положения заняла частное положение, то это значительно облегчит решение многих метрических задач.

Частных положений прямой - два (прямая уровня и проецирующая прямая), частных положений плоскости - тоже два (плоскость уровня и проецирующая плоскость). Отсюда следует, что должны существовать четыре исход­ных задачи преобразования комплексного чертежа, в результате которых:

1. Прямая общего положения становится прямой уровня.

2. Прямая общего положения становится проецирующей прямой.

3. Плоскость общего положения становится проецирующей плоскостью.

4. Плоскость общего положения становится плоскостью уровня.

Для решения этих задач будем использовать метод замены плоскостей проекций, хотя каждая из них могла бы быть решена и методом вращения, и методом плоскопараллельного переноса.

 

Задача 1. Преобразовать прямую общего положения АВ в прямую уровня (рис. 40).

Решение. Для решения этой задачи введем новую фронтальную плоскость проекций П₄, расположенную параллельно горизонтальной проекции А₁В₁ прямой АВ. Поскольку при введении новой фронтальной плоскости про­екций координаты Z точек А и В не должны измениться, дальнейшие построения ясны из чертежа. Отметим, что проекция А₄В₄ представляет собой натуральную величину отрезка АВ.

Другими словами, решение исходной задачи 1 преобразования ком­плексного чертежа представляет собой ещё один способ нахождения натуральной величины отрезка прямой общего положения.

Задача 2. Прямую общего положения преобразовать в положение проецирующей прямой (рис. 41).

Решение. Задача решается за два преобразования, поскольку здесь понадобится делать две замены плоскостей проекций: первой заменой прямая обще­го положения переводится в положение прямой уровня, а второй заменой полу­ченная прямая уровня переводится в проецирующую прямую. Первое преобра­зование - решение первой исходной задачи преобразования. Так как вводимая во втором преобразовании плоскость проекций П₅ - новая горизонтальная плоскость проекций, точка А₅ располагается на линии проекционной связи А₄А₅ на расстоянии, равном величине координаты У точки А в системе плоскостей проекций П₁/П₄.

Зная решение этой задачи, можно найти:

- расстояние между параллельными прямыми;

- расстояние между скрещивающимися прямыми;

- расстояние от точки до плоскости;

- натуральную величину двугранного угла (если линию пересечения двух плоскостей представить в виде проецирующей прямой).

 

 

Задача 3. Перевести плоскость общего положения, заданную треугольником АВС, в проецирующую плоскость (рис. 42).

 

Решение. Любую плоскость, заданную любым способом, можно представить как множество соответствующих прямых уровня, либо её горизонталей, либо ее фронталей. Поэтому преобразования нужно проводить таким образом, чтобы прямые уровня плоскости спроецировались в точки. Тогда сама плоскость спроецируется в совокупность точек, располагающихся на одной прямой. Следовательно, если в заданной плоскости общего положения провести прямые какого-либо уровня, то, расположив новую плоскость проекций перпендикулярно к горизонтальной проекции горизонтали или к фронтальной проекции фронтали, получим соответствующую проецирующую плоскость (рис. 42).

Зная решение этой задачи и поступая аналогично, можно находить:

- расстояние от точки до плоскости;

- расстояние между плоскостью и параллельной ей прямой;

- расстояние между параллельными плоскостями.

 

 

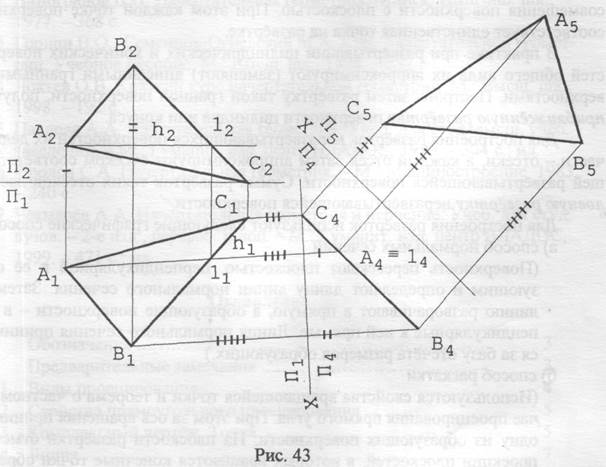
Задача 4. Плоскость общего положения, заданную треугольником АВС, перевести в положение плоскости уровня (рис. 43)

 

 

Решение. Задача решается за два преобразования: первым - плоскость общего положения переводится в положение проецирующей плоскости (решение исходной задачи 3, изложенное выше); вторым полученная проецирующая плоскость переводится в положение плоскости уровня (на рис. 42 - это плоскость горизонтального уровня). Точки А₅, В₅ и С₅ расположены от оси X, разделяющей плоскости П₄ и П₅ на расстояниях, равных величинам коорди­нат Y для точек А, В и С в системе плоскостей проекций П₁/П₄.

Зная решение этой задачи, можно находить натуральные величины плоских фигур, а следовательно - сторон многоугольников, плоских углов.

Заметим, что решение этой же задачи методом плоскопараллельного переноса приведено на рис. 39 в предыдущем разделе.

 

 

Развёртывание поверхностей

Развёртка поверхности - фигура, получающаяся после одностороннего совмещения поверхности с плоскостью. При этом каждой точке поверхности соответствует единственная точка на развёртке.

В практике при развёртывании цилиндрических и конических поверхностей общего вида их аппроксимируют (заменяют) вписанными гранными по­верхностями. Построив затем развёртку такой гранной поверхности, получают приближённую развёртку поверхности цилиндра или конуса.

Для построения развёрток неразвёртывающихся поверхностей их делят на части - отсеки, а каждый отсек затем аппроксимируют отсеком соответствующей развёртывающейся поверхности. Сумма развёрток таких отсеков даёт ус­ловную развёртку неразвёртывающейся поверхности.

Для построения развёрток используют следующие графические способы:

а) способ нормальных сечений

(Поверхность пересекают плоскостью, перпендикулярной к её образующим и определяют длину линии нормального сечения. Затем эту линию разворачивают в прямую, а образующие поверхности - в перпендикулярные к ней прямые. Линия нормального сечения принимает­ся за базу отсчёта размеров образующих.)

б) способ раскатки

(Используются свойства вращающейся точки и теорема о частном случае проецирования прямого угла При этом за ось вращения принимают одну из образующих поверхности. На плоскости развёртки отмечают проекции плоскостей, в которых вращаются конечные точки образую­щих поверхности. Зная расстояния между конечными точками, на плоскости развёртки находят эти точки и сами образующие.)

в) способ триангуляции

(Развёртываемая поверхность аппроксимируется многогранной поверхностью с треугольными гранями. Определяют размеры сторон ка­ждой грани. Общая развёртка представляет собой сумму развёрток треугольников-граней.)

Более подробное описание каждого из этих методов можно найти в литературе.

 

 

Библиографический список

 

1. Бубенников А.В. Начертательная геометрия. - М.: Высш. шк., 1985. - 288с.

2. Виноградов В.Н. Начертательная геометрия. Минск: Вышэйш. шк., 1977.-368 с.

3. Гордон В.О., Семенцов-Огиевский М.А. Курс начертательной геометрии. Учебное пособие. М.: Высш. шк., 1998. - 272 с.

4. Локтев О.В. Краткий курс начертательной геометрии. М.: Высш. шк., 1998. - 192 с.

5. Павлова А.А. Начертательная геометрия: Учеб. для студ. высш. учеб, заведений. - М.: Гуманит. изд. центр ВЛАДОС, 1999. - 304 с.: ил.

6. Фролов С.А. Начертательная геометрия. -М.: Машиностроение, 1983. -240с.

7. Чекмарёв А.А. Начертательная геометрия и черчение: Учеб. для студ.вузов. - 2-е изд., перераб. и доп. -М.: Гуманит. изд. центр ВЛАДОС,1999.-471 с.: ил.