А. Перпендикулярность двух прямых,

Решим следующую задачу:

Через точку М провести прямую, перпендикулярную отрезку АВ. Сколько возможно решений, и какие они могут быть (рис. 35)?

 

Обратим внимание на прямую АВ. Это - фронталь. На основании только что сформулированной теоремы на фронтальной плоскости проекций можно из точки М₂ провести прямую n₂, перпендикулярную А₂В₂:

n М ^ n ┴АВ => n₂ М₂ ^ n₂ ┴А₂В₂.

 

Могут существовать два варианта решения, в зависимости от того, как расположены прямые n и АВ по отношению друг к другу.

 

1. Если п и АВ пересекаются, l₂ — фронтальная проекция их точки пересечения 1. Горизонтальная проекция 1₁ точки 1 может быть найдена по принадлежности к прямой АВ и тем самым определится единственное положение прямой п (другими словами, задача имеет единственное ре­шение):

1 = n АВ => 1₂ = п₂ А₂В₂ => 1₁ = 1₁1₂ А₁В₁ => n₁ = М₁ l₁

 

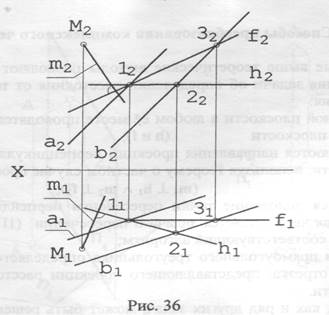
2. Если п и АВ - не пересекаются, то есть п и АВ - скрещивающиеся прямые, тогда прямые п и АВ общих точек не имеют. Все прямые, скрещивающиеся с АВ под прямым углом, будут располагаться в плоскости, проходящей через точку М и перпендикулярной к отрезку АВ. Посколь­ку через точку в плоскости можно провести бесконечное множество прямых, решений будет бесконечное множество. На комплексном чер­теже все фронтальные проекции таких прямых будут совпадать с п₂, горизонтальные проекции их будут изображаться пучком прямых, про­ходящих через точку М₁. На рис. 35 одна из таких прямых, m₁, показана пунктиром.

Б. Перпендикулярность прямой и плоскости.

Общий геометрический признак перпендикулярности прямой и плоскости (прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым этой плоскости) в начертательной геометрии звучит так:

если прямая перпендикулярна плоскости, то про­екции этой прямой перпендикулярны одноимен­ным проекциям прямых уровня этой плоскости.

Чтобы лучше себе это представить, решим еще одну задачу:

плоскость S задана параллельными прямыми а и b. Из точки М опустить на эту плоскость перпендикуляр т (рис. 36).

Использование теоремы о частном случае проецирования прямого угла даёт возможность предложить следующий план решения задачи:

1. В плоскости Σ(а//b) в любом месте строим её фронталь и горизонталь;

2. Через точки М₁ и M₂проводим перпендикуляры к h₁ и f₂ (к горизонталь­
ной проекции горизонтали и к фронтальной проекции фронтали), то
есть: m₁ ┴ h₁ ^ m₂ ┴ f₂.

 

Заметим, что точку пересечения прямой и плоскости мы не находили, да это и не требовалось по условию задачи.

Чтобы лучше себе представить, что мы проделали, уясним, что эта точка пересечения и не будет в общем случае находится в месте пересечения проведенной нами фронтали и горизонтали плоскости. Но если бы мы из точки пере­сечения фронтали и горизонтали плоскости восставили к ней перпендикуляр, то все перпендикуляры к плоскости, проведенные к ней из любой точки, были бы параллельны этому восставленному перпендикуляру.

При решении многих задач о перпендикулярности прямой и плоскости следует иметь в виду и то обстоятельство, что плоскость и перпендикуляр к ней - «жёсткая» система: если плоскость - общего положения, то и перпендикуляр к ней - прямая общего положения; если плоскость - частного положе­ния, то и перпендикуляр к ней - прямая частного положения.

В. Перпендикулярность двух плоскостей.

Признак перпендикулярности двух плоскостей можно сформулировать следующим образом:

плоскость Σ перпендикулярна плоскости Ω если плоскость Σ проходит через прямую, перпендикулярную плоскости Ω.

Представление решений многих задач на комплексном чертеже облегчает и следующее обстоятельство:

если плоскости Σ и Ω перпендикулярны, то перпендикулярны и соответствующие проекции их прямых уровня: h₁^Σ ┴ h₁^Ω ^ f₂^Σ ┴ f₂^Ω

где h₁ – горизонтальная проекция горизонтали;

f₂ - фронтальная проекция фронтали,

а Σ и Ω определяют принадлежность их к той или иной плоскости.

 

 

12. Способы преобразования комплексного чертежа

Изложенные выше теоретические выводы позволяют наметить следующий план решения задачи об определении расстояния от точки до плоскости общего положения:

1) в заданной плоскости в любом её месте проводятся фронталь и горизонталь плоскости (h и f);

2) определяются направления проекций перпендикуляра m к заданной плоскости, используя теорему о частном случае проецирования прямо­го угла (m₁ ┴ h₁ ^m₂ ┴ f₂.);

3) находится положение точки пересечения перпендикуляра с плоскоcтью, для чего решается задача о пересечении (1ГПЗ, случай 3), ис­пользуя соответствующий алгоритм;

4) методом прямоугольного треугольника определяется натуральная величина отрезка, представляющего проекции расстояния от точки до плоскости.

Эта задача, как и ряд других задач, может быть решена проще, если каким-либо образом преобразовать комплексный чертёж так, чтобы хотя бы один из заданных геометрических образов стал образом частного положения.