Главные выводы, касающиеся метода проецирования.

1. При заданной системе плоскостей проекций определена
пространственная система координат Охуz, в которой положение любой точки может быть однозначно определено тремя координатами. Например, для точки А её положение определено как А (Х_А, У_А, Z_А).

2. Проекция любой точки на комплексном чертеже определяется
двумя координатами из этих трёх:

- фронтальная проекция А₂(Х_А, Z_А);

- горизонтальная проекция а₁(х_а, У_А);

- профильная проекция А₃(У_A, Z_А).

Главные выводы, вытекающие из обзора геометрических образов (точка, линия, поверхность, плоскость).

1. Главная проекция прямой, плоскости или поверхности - это проекция вырожденная:

- для прямой - в точку;

- для плоскости — в прямую линию;

- для поверхности - в её основание.

2. Наличие у геометрического образа главной проекции является
признаком того, что данный геометрический образ - проецирующий.

3. Основное свойство главной проекции проецирующего образа
заключается в том, что любая точка или линия, принадлежащие прямой, плоскости или поверхности, одной из проекций будут иметь проекцию точки или линии, совпадающие с главной проекцией прямой, плоскости или поверхности.

4. Из всего многообразия поверхностей проецирующими образами могут быть только прямая призма или прямой цилиндр.

Принадлежность

В литературе задачи о принадлежности часто относят к позиционным задачам. Можно выделить три разновидности задач о принадлежности, из которых следует:

1. Определить, принадлежит ли данная точка линии, поверхности или плоскости.

2. По заданной проекции точки или линии определить вторую, а иногда и третью проекцию либо точки, принадлежащей
линии, плоскости или поверхности, либо линии, принадлежащей плоскости или поверхности.

3. Задать произвольную точку, принадлежащую заданной ли­нии, поверхности, плоскости, либо задать произвольную ли­нию, принадлежащую заданной поверхности или плоскости. Любая из разновидностей задач о принадлежности решается, в принципе, исходя из одних и тех же соображений. Рассмотрим подробнее возможные виды принадлежности и способы решения связанных с ними задач.

А. Принадлежность точки линии.

Основное положение в этом случае таково:

точка принадлежит прямой, если ее проекции принад­лежат одноименным проекциям этой прямой (рис. 17).

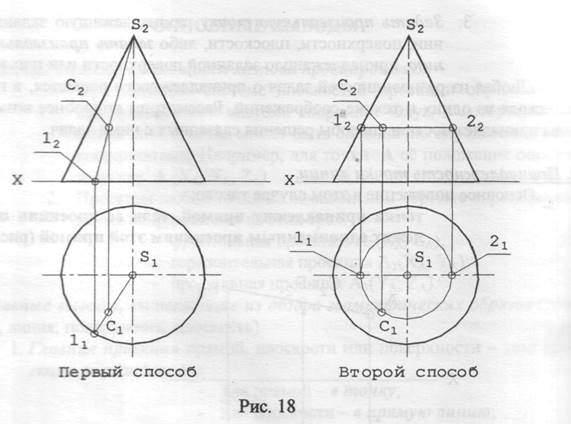
(На рис. 17 точка С принадлежит прямой АВ, а точка D - АВ не принадлежит).

Б. Принадлежность точки поверхности.

Основное положение при решении задач для этого варианта принадлежности следующее:

точка принадлежит поверхности, если она принадле­жит какой-либо линии этой поверхности.

В этом случае линии надо выбирать наиболее простыми, чтобы легче было построить проекции такой линии, затем использовать то обстоятельство, что проекции точки, лежащие на поверхности, должны принадлежать одноименным проекциям линии этой поверхности.

Пример 1. Определить, принадлежит ли точка С поверхности конуса (рис. 18).

 

 

 

Здесь есть два пути решения, поскольку можно провести две простейших линии, принадлежащих конической поверхности. В первом случае — проводится прямая линия - образующая конической поверхности S1 так, чтобы она проходила через какую-либо заданную проекцию точки С. Тем самым предполагаем, что точка С принадлежит образующей S1 конической поверхности, а следовательно - самой конической поверхности. В этом случае одноименные проекции точки С должны лежать на соответствующих проекциях этой образующей.

Другая простейшая линия - окружность с диаметром 1-2 (радиус этой окружности - отсчитывается от оси конуса до очерковой образующей). Этот

факт известен еще из школьного курса геометрии: при пересечении кругового конуса плоскостью, параллельной его основанию, или перпендикулярной к его оси, в сечении будет получаться окружность. Второй способ решения позволяет найти недостающую проекцию точки С, заданной своей фронтальной проекцией, принадлежащей поверхности конуса и совпадающей на чертеже с осью вращения конуса, без построения третьей проекции. Всегда следует иметь в виду, видима или не видима точка, лежащая на поверхности конуса (в случае, если она не видна, соответствующая проекция точки будет заключена в скобки).

Очевидно, что в нашей задаче точка С принадлежит поверхности, поскольку проекции точки принадлежат одноимённым проекциям линий, использованных для решения как при первом, так и при втором способе решения.

 

В. Принадлежность линии поверхности.

Основное положение:

линия принадлежит поверхности, если все тс линии принадлежат заданной поверхности.

 

Это означает, что в данном случае принадлежности должна быть несколько раз решена задача о принадлежности точки поверхности.

Г. Принадлежность прямой плоскости

Что касается принадлежности прямой плоскости, то здесь справедливы высказанные выше соображения относительно принадлежности к поверхности, с тем лишь условием, что для плоскости простейшей линией всегда является прямая, а положение прямой в пространстве однозначно определяется положением двух принадлежащих ей точек.

 

Пример 2. Задать произвольную точку К, принадлежащую плоскости, заданной двумя пересекающимися прямыми а и b (рис. 19).

Решение. Можно взять какую-либо точку К, провести через нее прямую m, про которую точно можно сказать, что она принадлежит заданной плоскости, а потом определить вторую проекцию первоначально заданной произволь­ной точки. Можно сразу провести произвольную прямую плоскости, а затем определить положение произвольной точки плоскости, задав соответствующие проекции этой точки, принадлежащие проведенной прямой.