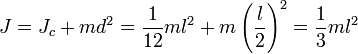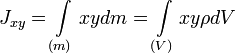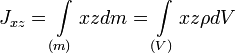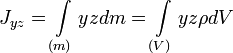Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Главный вектор и главный момент сил инерции.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Из первого уравнения в (6) следует, что Ф = -(Fe+ Re). Но по теореме о движении центра масс главный вектор внешних сил системы (Fe+ Re) равен MaC, поэтому
где aC - ускорение центра масс системы в инерциальной системе координат, принимаемой за неподвижную, или абсолютное ускорение центра масс. То есть главный вектор сил инерции системы материальных точек равен массе системы, умноженной на величину абсолютного ускорения центра масс, и направлен противоположно этому ускорению. Из второго уравнения в (6) находим, что главный момент сил инерции относительно произвольного центра O равен MO(Фi) = -(MO(Fie) + MO(Rie)). Если центр O неподвижен, то согласно теореме об изменении момента количеств движения относительно неподвижного центра MO(Fie) + MO(Rie) = dKO/ dt. Поэтому
то есть главный момент сил инерции системы относительно неподвижного центра O равен взятой со знаком минус производной по времени от момента количеств движения системы относительно того же центра. Соответственно, главный момент сил инерции относительно неподвижной оси, например оси z, равен
Если центр подвижен, то согласно той же теореме, но уже относительно подвижного центра A,
где KA - момент количеств движения системы в абсолютном движении относительно подвижного центра A. Если подвижный центр совпадает с центром масс C системы материальных точек и VA= VC, то из (11) следует, что
где KC - момент количеств движения системы относительно центра масс в абсолютном движении. Учитывая, что момент количеств движения системы относительно цен-тра масс в абсолютном и относительном движении одинаковы, из (12) получаем
где K rC - момент количеств движения системы в ее относительном движении вокруг центра масс. Таким образом, из формул (12) и (13) следует, что главный момент сил инерции системы относительно ее центра масс равен взятой со знаком минус производной по времени от момента количеств движения системы относительно центра масс, вычисленного в абсолютном или относительном движении. Приведение сил инерции твердого тела. Согласно теореме Пуансо, доказанной в статике твердого тела, система сил инерции твердого тела приводится к одной силе или главному вектору, приложенному в центре приведения, и одной паре сил, момент которой равен главному моменту сил инерции относительно центра приведения. Причем величина и направление главного вектора не зависят от выбора центра приведения (главный вектор является инвариантом системы сил), а величина и направление главного момента изменяются при смене центра приведения. По следствию принципа Даламбера (6) центром приведения является центр O (подвижный или неподвижный), поэтому главный вектор сил инерции твердого тела приложен в этом центре, а его величина и направление определяется по формуле (8) и не зависят от выбора центра приведения. Главный момент MO(Фi) сил инерции твердого тела также приложен в центре приведения, но зависит от выбора центра приведения. На рис. 52, a показан результат приведения сил инерции твердого тела, когда за центр приведения выбран центр O, а на рис 52, b показан тот же результат, но когда за центр приведения выбран центр масс тела C. Главный вектор сил инерции не изменил ни направления, ни величины, сменилась только точка его приложения, но зато изменился главный момент сил инерции и MO(Фi) <> MO(Фi). То есть главный вектор сил инерции совсем не обязательно проходит через центр масс тела, хотя по величине он всегда равен произведению массы тела на абсолютное ускорение центра масс и направлен противоположно этому ускорению.
Билет №7 1. Центр масс системы материальных точек. Теорема о его движении Центр масс - геометрическая точка, характеризующая движение тела или системы частиц как целого.
Для случая непрерывного распределения масс:
Теорема о движении центра масс: произведение массы системы на ускорение её центра масс равно геометрической сумме всех действующих на систему внешних сил.
2. Возьмем абсолютно твердое тело, вращающееся около неподвижной оси z, проходящей через него (рис. 1). Разобьем тело на маленькие объемы с элементарными массами m1, m2,..., mn, находящиеся на расстоянии r1, r2,..., rn от оси.
При вращении твердого тела относительно неподвижной оси каждый из его элементарных объемов массами mi опишет окружность соответствующих радиусов ri; при этом объем будет иметь соответствующую линейную скорость vi. Но так как мы рассматриваем абсолютно твердое тело, то угловая скорость вращения этих объемов одинакова:
Кинетическую энергию вращающегося тела найдем как сумму кинетических энергий его элементарных объемов:
Используя выражение (1), получаем В качеcтве примера напишем формулу для плоского движения тела, например цилиндра, скатывающегося с наклонной плоскости без скольжения. Его энергия движения складывается из энергии поступательного движения и энергии вращения:
Билет №8 1. 2. Переносная и кориолисова сила инерции. Переносной силой инерции, действующей на материальную точку массы m в неинерциальной системе отсчета, называется сила, равная произведению массы этой материальной точки на взятое с обратным знаком ее переносное ускорение
Кориолисовой силой инерции, действующей на материальную точку массы m в неинерциальной системе отсчета, называется сила, равная произведению массы этой материальной точки на взятое с обратным знаком ее кориолисово ускорение Билет №9 1. Теорема обизменении кинетического момента механической системы относительно ее центра масс 2. Виртуальные (возможные) скорости точек механической системы Для одной материальной точки возможное перемещение вводится как бесконечно малое воображаемое перемещение, допускаемое связями в данный момент времени; это – векторная величина, совпадающая по направлению с возможной скоростью точки. Для механической системы возможное перемещение определяется как перемещение системы в бесконечно-близкое положение, допускаемое связями в данный момент времени. При этом каждая точка системы, как и в случае отдельной точки, получает возможное перемещение, совпадающее по направлению с ее возможной скоростью. Так для рычага (рис. 6.1) возможное перемещение определяется поворотом на бесконечно-малый угол Рис 6.1 Для кривошипно-ползунного механизма (рис. 6.2) возможное перемещение есть бесконечно малое смещение звеньев механизма из заданного положения. При этом точка направленное вдоль возможной скорости точки Число независимых возможных перемещений системы называется числом ее степеней свободы. Например, одну степень свободы имеет точка, перемещающаяся по прямой или по заданной криволинейной траектории. Также одну степень свободы имеет тело, вращающееся вокруг неподвижной оси. Для определения числа степеней свободы системы с голономными связями (Связи называются голономными, если они накладывают ограничения на положения тел и точек системы.) поступают следующим образом. Вначале у системы исключают одну степень свободы (для этого закрепляют точку, движущуюся по заданной линии, или закрепляют вращающееся тело). Если после этого подвижность системы будет полностью устранена значит, у системы одна степень свободы. Если же подвижность сохранится, то исключают еще одну степень свободы; и так далее до полного устранения подвижности системы (до полной остановки системы). Число таких исключений равно числу степеней свободы системы. Билет 10 1. Осевые и центробежные моменты инерции твердого тела. Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
где: · mi — масса i -й точки, · ri — расстояние от i -й точки до оси. Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.
где: · · · Если тело однородно, то есть его плотность всюду одинакова, то
Теорема Гюйгенса — Штейнера Момент инерции твёрдого тела относительно какой-либо оси зависит от массы, формы и размеров тела, а также и от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:
где Например, момент инерции стержня относительно оси, проходящей через его конец, равен:
Центробежный момент инерции Центробежными моментами инерции тела по отношению к осям прямоугольной декартовой системы координат называются следующие величины:
где x, y и z — координаты малого элемента тела объёмом dV, плотностью ρ и массой dm. Ось OX называется главной осью инерции тела, если центробежные моменты инерции Jxy и Jxz одновременно равны нулю. Через каждую точку тела можно провести три главные оси инерции. Эти оси взаимно перпендикулярны друг другу. Моменты инерции тела относительно трёх главных осей инерции, проведённых в произвольной точке O тела, называются главными моментами инерции тела. Главные оси инерции, проходящие через центр масс тела, называются главными центральными осями инерции тела, а моменты инерции относительно этих осей — его главными центральными моментами инерции. Ось симметрии однородного тела всегда является одной из его главных центральных осей инерции. Билет 11
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 2043; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.175.166 (0.009 с.) |








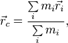 где
где 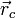 — радиус-вектор центра масс,
— радиус-вектор центра масс, 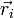 — радиус-вектор i -й точки системы,
— радиус-вектор i -й точки системы, 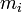 — масса i -й точки.
— масса i -й точки.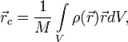
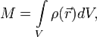 где
где 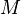 — суммарная масса системы,
— суммарная масса системы, 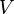 — объём,
— объём, 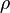 — плотность.
— плотность.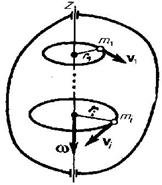
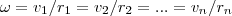 (1)
(1)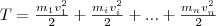
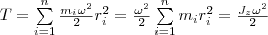
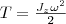 (2)
(2) 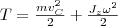




 вокруг точки опоры. При этом возможное перемещение
вокруг точки опоры. При этом возможное перемещение 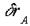 точки
точки  направлено перпендикулярно рычагу, т.е. в сторону ее возможной скорости.
направлено перпендикулярно рычагу, т.е. в сторону ее возможной скорости.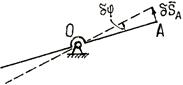 рис 6.2
рис 6.2 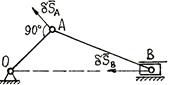
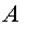 имеет возможное перемещение, направленное вдоль ее возможной скорости, т.е. перпендикулярно кривошипу
имеет возможное перемещение, направленное вдоль ее возможной скорости, т.е. перпендикулярно кривошипу 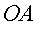 ; а точка
; а точка 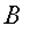 имеет возможное перемещение,
имеет возможное перемещение,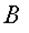 .
.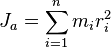 ,
,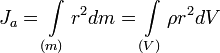 ,
,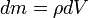 — масса малого элемента объёма тела
— масса малого элемента объёма тела  ,
, — расстояние от элемента
— расстояние от элемента 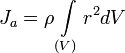
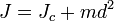 ,
, — полная масса тела.
— полная масса тела.