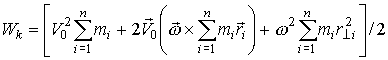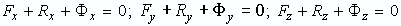Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон сохранения полной механической энергииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой посредством сил тяготения и сил упругости, остается неизменной. Это утверждение выражает закон сохранения энергии в механических процессах. Он является следствием законов Ньютона. Сумму E = Ek + Ep называют полной механической энергией. Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой консервативными силами, то есть силами, для которых можно ввести понятие потенциальной энергии.
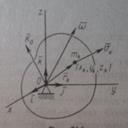
Билет 11 Выражение кинетического момента тела с одной неподвижной точкой через матрицу моментов инерции тела. Имеет твердое тело, одна из точек которого закреплена. Движение тела рассматривается относительно некоторой системы координат Оxyz. Кинетически момент относительно неподвижной точки: Где rk- радиус-вектор какой-либо точки тела. mk-масса точки. Vk-скорость этой точки относительно выбранной системы отсчета.
В проекциях на оси: Для проекции кинетического момента на ось Ox с учетом(2’) имеем: Суммы в (1’) представляют собой соответственно осевой и центробежные моменты инерции. Получаем: По (3)вычисляются проекции на оси координат кинетического момента тела относительно его закрепленной точки. Кинетический момент по проекциям определяется по формуле: Для неподвижных осей осевые и центробежные моменты инерции изменяются при вращении тела и, следовательно, зависят от времени вследствие изменения положения тела относительно этих осей. Если применить тензор инерции: И учесть правило умножения тензора на вектор столбец омега, то можно кратко выразить формулой: Упрощаем формулу (3)для проекций: В этом случае проекции кинетического момента вычисляются так же, как и в случае, если бы каждая из главных осей инерции была неподвижной осью вращения тела. Главные оси инерции для неподвижной точки О обычно подвижные оси, скрепленные с самим вращающимся телом. Только такие оси могут быть главными в течении всего времени вращения тела. Другие подвижные или неподвижные оси могут быть главными только в отдельные моменты времени. Кинетическая энергия поступательного движения Кинетической энергией системы называется скалярная величина Т, равная арифметической сумме кинетических энергий всех точек системы
Кинетическая энергия является характеристикой и поступательного и вращательного движения системы, поэтому теоремой об изменении кинетической энергии особенно часто пользуются при решении задач. Если система состоит из нескольких тел, то ее кинетическая энергия равна, очевидно, сумме кинетических энергий этих тел:
Кинетическая энергия – скалярная и всегда положительная величина. Найдем формулы для вычисления кинетической энергии тела в разных случаях движения. 1. Поступательное движение. В этом случае все точки тела движутся с одинаковыми скоростями, равными скорости движения центра масс. То есть, для любой точки
или
Таким образом, кинетическая энергия тела при поступательном движении равна половине произведения массы тела на квадрат скорости центра масс. От направления движения значение Т не зависит.
Билет 12 Дифференциальное уравнение вращения твердого тела вокруг неподвижной оси Дифференциальное уравнение имеет вид: где Уравнение (2.6) получается из уравнения (2.4) теоремы путём подстановки в него формулы (2.3).
Интегрируя уравнение (2.6), можно определить закон вращения тела. Методика решения подобных задач: – изображаем тело в произвольном положении; показываем внешние силы, действующие на тело; показываем ось – находим сумму моментов внешних сил относительно оси – вычисляем, если не задан, момент инерции тела – составляем уравнение (2.6), интегрируя это уравнение, определяем закон вращения тела.
ПОТЕНЦИАЛЬНЫЕ СИЛЫ Поле сил, остающееся постоянным во времени, называется стационарным. В стационарном силовом поле сила, действующая на частицу, зависит только от ее положения. Работа, которую совершают силы поля при перемещении частицы из точки 1 в точку 2, зависит, вообще говоря, от траектории, по которой перемещается частица из начального положения в конечное. Вместе с тем, имеются стационарные силовые поля, в которых работа, совершаемая над частицами силами поля, не зависит от формы траектории между точками 1 и 2. Силы, обладающие таким свойством, называются потенциальными или консервативными, а соответствующее поле сил – потенциальным полем. Примером потенциальных сил являются упругие силы, сила тяжести.
Билет
1) Для внутренних сил механической системы имеет место свойство: главный вектор и главный момент внутренних сил механической системы равны нулю.
Это следует из того, что внутренние силы есть силы взаимодействия между точками системы, которые попарно равны и направлены в противоположные стороны. 2) Если все силы системы потенциальны, то обобщенные силы системы выражаются через потенциальную энергию системы как Qj = -дП / дqj, а уравнения Лагранжа второго рода запишутся в виде
Так как потенциальная энергия не зависит от обобщенных скоростей, то. Введем в рассмотрение функцию
которую называют функцией Лагранжа или кинетическим потенциалом. Тогда уравнения Лагранжа в случае потенциальных сил запишутся так:
Билет 16. 1. Tеорема об изменении кинетической энергии механической системы в дифференциальной форме Изменение кинетической энергии механической системы на некотором ее перемещении равно сумме работ внешних и внутренних сил, приложенных к точкам системы, на том же перемещении.
2. Удерживающие и стационарные связи Если функция
Если связь задаётся равенством, то говорят, что такая связь — удерживающая или двусторонняя:
Билет 17 1 Tеорема об изменении кинетической энергии механической системы Кинетической энергией системы называют сумму кинетических энергий всех тел, входящих в систему. Для определённой таким образом величины справедливо утверждение: Изменение кинетической энергии системы равно работе всех внутренних и внешних сил, действующих на тела системы.
2 Голономные связи Голоно́мная связь — механическая связь, налагающая ограничения только на положения (или перемещения) точек и тел системы. Математически выражается в виде равенства:
Билет 18 1.Принцип Эйлера-Даламбера для материальной точки Согласно данному принципу, для каждой i-той точки системы верно равенство 2 кинетическая энергия тела при плоском движении
Билет 19 Уравнения кинетостатики. Кинетостатика - раздел механики, в котором рассматриваются способы решения динамических задач с помощью аналитических или графических методов статики. В основе К. лежит Д'Аламбера принцип, согласно которому уравнения движения тел можно составлять в форме уравнений статики, если к фактически действующим на тело силам и реакциям связей присоединить силы инерции. Методы К. находят применение при решении ряда динамических задач, особенно в динамике машин и механизмов. уравнения кинетостатики для материальной точки:
где F, R, Ф - главные векторы активных сил, реакций связей и сил инерции; Fz, Rz, Фz- главные моменты активных сил, реакций связей и сил инерции относительно точки О1
|
||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 1103; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |


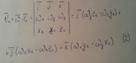 формула эйлера
формула эйлера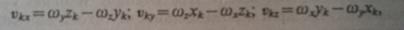


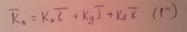
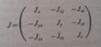
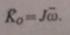 .
.
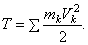

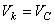


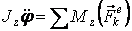 , (2.6)
, (2.6) – угловое ускорение тела.
– угловое ускорение тела.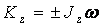 (2.3)
(2.3)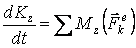 (2.4)
(2.4) , направленную по оси вращения тела в ту сторону, откуда вращение видно происходящим против часовой стрелки;
, направленную по оси вращения тела в ту сторону, откуда вращение видно происходящим против часовой стрелки;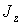 ;
;
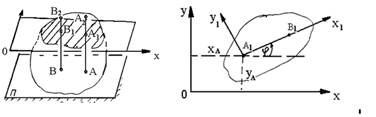 Рассмотрим сечение тела какой-нибудь плоскостью OXY, параллельной неподвижной плоскости П (рис.1).При плоскопараллельном движении все точки тела, лежащие на прямой
Рассмотрим сечение тела какой-нибудь плоскостью OXY, параллельной неподвижной плоскости П (рис.1).При плоскопараллельном движении все точки тела, лежащие на прямой 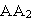 , перпендикулярной к сечению, т.е. к плоскости П, движутся тождественно. Поэтому для изучения движения всего тела достаточно изучить, как движется сечение тела в плоскости OXY. В дальнейшем будем плоскость OXY совмещать с плоскостью рисунка, а вместо всего тела изображать только его сечение. Положение сечения в плоскости OXY определяется положением какого-нибудь проведенного в этом сечении отрезка АВ (рис.2). Положение отрезка АВ можно определить, зная координаты
, перпендикулярной к сечению, т.е. к плоскости П, движутся тождественно. Поэтому для изучения движения всего тела достаточно изучить, как движется сечение тела в плоскости OXY. В дальнейшем будем плоскость OXY совмещать с плоскостью рисунка, а вместо всего тела изображать только его сечение. Положение сечения в плоскости OXY определяется положением какого-нибудь проведенного в этом сечении отрезка АВ (рис.2). Положение отрезка АВ можно определить, зная координаты 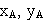 точки А и угол
точки А и угол 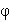 , который от-резок АВ образует с осью x. Точку А, выбранную для определения положения сечения, называют полюсом. При движении тела величины
, который от-резок АВ образует с осью x. Точку А, выбранную для определения положения сечения, называют полюсом. При движении тела величины 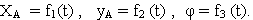 (1.74)
Уравнения определяющие закон происходящего движения, называются уравнениями плоскопараллельного движения твердого тела.
2.Главный момент всех внутренних сил системы(относительно всякого выбранного центра) в любой момент времени равен нулю (MOi=0).M-вектор.
(1.74)
Уравнения определяющие закон происходящего движения, называются уравнениями плоскопараллельного движения твердого тела.
2.Главный момент всех внутренних сил системы(относительно всякого выбранного центра) в любой момент времени равен нулю (MOi=0).M-вектор.
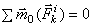 или
или 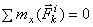 .
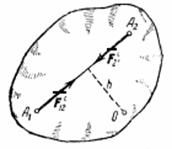
Уравновешенными внутренние силы будут тогда, когда рассматриваемая система представляет собою абсолютно
твердое тело. Действительно, если взять произвольный центр О, то из рис. видно, что
.
Уравновешенными внутренние силы будут тогда, когда рассматриваемая система представляет собою абсолютно
твердое тело. Действительно, если взять произвольный центр О, то из рис. видно, что 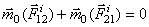 .
.
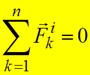
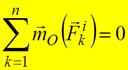 .
.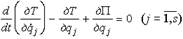
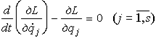
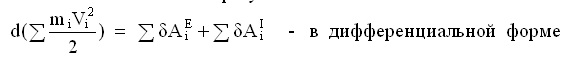
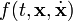 зависит явно от времени, то говорят, что связь — нестационарная или реономная; если же эта функция не зависит явно от времени, то говорят, что эта связь — стационарная или склерономная.
зависит явно от времени, то говорят, что связь — нестационарная или реономная; если же эта функция не зависит явно от времени, то говорят, что эта связь — стационарная или склерономная.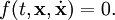

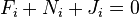 , где
, где  — действующая на эту точку активная сила,
— действующая на эту точку активная сила, 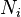 — реакция наложенной на точку связи,
— реакция наложенной на точку связи, 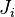 — сила инерции, численно равная произведению массы
— сила инерции, численно равная произведению массы 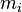 точки на её ускорение
точки на её ускорение 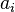 и направленная противоположно этому ускорению (
и направленная противоположно этому ускорению (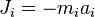 )
)