
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Описание экспериментальной установки. Механическая конструкция прибора
Описание экспериментальной установки. Механическая конструкция прибора
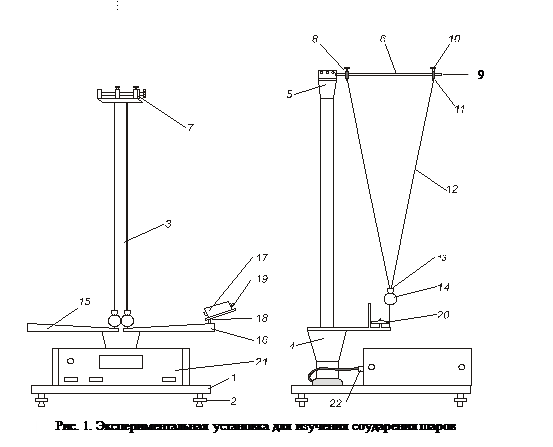
Общий вид прибора для исследования столкновения шаров FPM-08 представлен на рис.1. Основание 1 оснащено регулируемыми ножками (2), которые позволяют устанавливать горизонтальное положение основания прибора. В основании закреплена колонна 3, к которой перекреплены нижний 4 и верхний 5 кронштейны. На верхнем кронштейне крепится стержень 6 и винт 7, служащие для установки расстояния между шарами. На стержнях 6 помещены передвигаемые держатели 8 с втулками 9, фиксированные при помощи болтов 10 и приспособленные к прикреплению подвесов 11.    Через подвесы 11 проходят провода 12, подводящие напряжение к подвесам 13, а через них к шарам 14. После ослабления винтов 10 и 11 можно добиться центрального соударения шаров. Через подвесы 11 проходят провода 12, подводящие напряжение к подвесам 13, а через них к шарам 14. После ослабления винтов 10 и 11 можно добиться центрального соударения шаров.
На нижнем кронштейне закреплены угольники со шкалами 15,16, а на специальных направляющих - электромагнит 17. После отвинчивания болтов 18,19 электромагнит можно передвигать вдоль правой шкалы и фиксировать высоту его установки, что позволяет изменять начальный первого шара. К основанию прибора прикреплён секундомер FRM-16 21,передающий через разъем 22 напряжение к шарам и электромагниту. На лицевой панели секундомера FRM-16 находятся следующие манипуляционные элементы: 1. W1 (Сеть)- выключатель сети. Нажатие этой клавиши вызывает включение питающего напряжения; 2. W2 (Сброс) – сброс измерителя. Нажатие этой клавиши вызывает сбрасывание схем секундомера FRM-16. 3. W3 (Пуск) –управление электромагнитом. Нажатие этой клавиши вызывает освобождение электромагнита и генерирование в схеме секундомера импульса как разрешение на измерения. ВЫПОЛНЕНИЕ РАБОТЫ Упражнение №1. Проверка закона сохранения импульса при неупругом центральном ударе. Определение коэффициента восстановления кинетической энергии. Для изучения неупругого удара берутся два стальных шара, но на одном шаре в месте, где происходит удар, прикрепляется кусочек пластилина. Таблица №1.
1. Получите у преподавателя начальное значение угла отклонения первого шара 2. Установите электромагнит так, чтобы угол отклонения первого шара (меньшей массы) соответствовал заданному значению 3. Отклоните первый шар на заданный угол, нажмите на клавишу <ПУСК> и произведити отсчет угла отклонения второго шара 4. Массы шаров 5. По формуле 6. По формуле 7. По формуле 8. По формуле 9. По формуле 10. По формуле 11. По формуле 12. Запишите интервал для импульса системы после столкновения в виде Найдите отношение проекции импульса системы после неупругого удара Упражнение №2. Проверка закона сохранения импульса и механической энергии при упругом центральном ударе. Определение силы взаимодействия шаров при столкновении.
Для изучения упругого удара берутся два стальных шара. Шар, который отклоняют к электромагниту, считается первым. Таблица №2.
1. Получите у преподавателя начальное значение угла отклонения первого шара 2. Установите электромагнит так, чтобы угол отклонения первого шара (меньшей массы) соответствовал заданному значению 3. Отклоните первый шар на заданный угол, нажмите на клавишу <ПУСК> и произведити отсчет углов отклонения первого шара 4. По формуле 5. По формуле 6. По формуле 7. По формуле 8. По формуле 9. По формуле 10. По формуле 11. По формуле 12. По формуле 13. По формуле 14. Запишите интервал для импульса системы после столкновения в виде 15. Запишите интервал для кинетической энергии системы после столкновения в виде Найдите отношение проекции импульса системы после упругого удара Найдите отношение кинетической энергии системы после упругого удара Сравните полученное значение величины силы взаимодействия КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Импульс и энергия, виды механической энергии. 2. Закон изменения импульса, закон сохранения импульса. Понятие о замкнутой механической системе. 3. Закон изменения полной механической энергии, закон сохранения полной механической энергии. 4. Консервативные и неконсервативные силы. 5. Удар, виды ударов. Запись законов сохранения для абсолютно упругого и абсолютно неупругого ударов. 6. Взаимопревращениемеханической энергии при свободном падении тела и упругих колебаниях.
Виды механической энергии Работа является мерой изменения энергии тела или системы тел. В механике различают следующие виды энергии: - Кинетическая энергия
где Т – кинетическая энергия, Дж m – масса точки, кг ν – скорость точки, м/с особенность: всегда является величиной положительной.
Виды потенциальной энергии
- Потенциальная энергия поднятой над Землёй материальной точки
П=mgh
особенность: может быть положительной, отрицательной и равной нулю в зависимости от выбора начального уровня отсчёта потенциальной энергии (см. рисунок)
П=mghц.Т.
где П – потенциальная энергия, Дж m – масса, кг g – ускорение свободного падения, м/с2 h – высота точки над нулевым уровнем отсчёта потенциальной энергии, м hц.т . - высота центра масс системы материальных точек или протяжённого тела над нулевым уровнем отсчёта потенциальной энергии, м
особенность: может быть положительной, отрицательной и равной нулю в зависимости от выбора начального уровня отсчёта потенциальной энергии - Потенциальная энергия деформированной пружины Δ х – величина деформации пружины, м
Особенность: всегда является величиной положительной. - Потенциальная энергия гравитационного взаимодействия двух материальных точек
M и m – массы точек, кг r – расстояние между ними, м особенность: всегда является величиной отрицательной (на бесконечности она принята равной нулю) Полная механическая энергия (это сумма кинетической и потенциальной энергии, Дж) Е = Т + П Коэффициент полезного действия (КПД) (характеризует экономичность двигателя, механизма или процесса)
η =
Связь A, N и η
Виды ударов Ударом называется кратковременное взаимодействие двух или более тел. Центральным (или прямым) называется удар, при котором скорости тел до удара направлены вдоль прямой, проходящей через их центры масс. (в противном случае удар называется нецентральным или косым) Упругим называется удар, при котором тела после взаимодействия движутся раздельно друг от друга. Неупругим называется удар, при котором тела после взаимодействия движутся как единое целое, то есть с одной и той же скоростью. Предельными случаями ударов являются абсолютно упругий и абсолютно неупругий удары.
ДИНАМИКА ТВЁРДОГО ТЕЛА Момент импульса твёрдого тела, вращающегося относительно неподвижной оси Кинетическая энергия твёрдого тела, вращающегося относительно неподвижной оси Кинетическая энергия твёрдого тела, вращающегося относительно оси, движущейся поступательно
Основное уравнение динамики вращательного движения механической системы: Векторная сумма моментов всех внешних сил, действующих на механическую систему относительно неподвижной точки О, равна скорости изменения момента импульса этой системы.
Основное уравнение динамики вращательного движения твёрдого тела: Векторная сумма моментов всех внешних сил, действующих на тело относительно неподвижной оси Z, равна произведению момента инерции этого тела относительно оси Z, на его угловое ускорение.
Теорема Штейнера: Момент инерции тела относительно произвольной оси, равен сумме момента инерции тела относительно оси параллельной данной и проходящей через центр масс тела, плюс произведение массы тела на квадрат расстояния между этими осями
Момент инерции материальной точки Элементарная работа момента сил при вращении тела вокруг неподвижной оси Работа момента сил при вращении тела вокруг неподвижной оси
Описание экспериментальной установки. Механическая конструкция прибора
Общий вид прибора для исследования столкновения шаров FPM-08 представлен на рис.1. Основание 1 оснащено регулируемыми ножками (2), которые позволяют устанавливать горизонтальное положение основания прибора. В основании закреплена колонна 3, к которой перекреплены нижний 4 и верхний 5 кронштейны. На верхнем кронштейне крепится стержень 6 и винт 7, служащие для установки расстояния между шарами. На стержнях 6 помещены передвигаемые держатели 8 с втулками 9, фиксированные при помощи болтов 10 и приспособленные к прикреплению подвесов 11.    Через подвесы 11 проходят провода 12, подводящие напряжение к подвесам 13, а через них к шарам 14. После ослабления винтов 10 и 11 можно добиться центрального соударения шаров. Через подвесы 11 проходят провода 12, подводящие напряжение к подвесам 13, а через них к шарам 14. После ослабления винтов 10 и 11 можно добиться центрального соударения шаров.
На нижнем кронштейне закреплены угольники со шкалами 15,16, а на специальных направляющих - электромагнит 17. После отвинчивания болтов 18,19 электромагнит можно передвигать вдоль правой шкалы и фиксировать высоту его установки, что позволяет изменять начальный первого шара. К основанию прибора прикреплён секундомер FRM-16 21,передающий через разъем 22 напряжение к шарам и электромагниту. На лицевой панели секундомера FRM-16 находятся следующие манипуляционные элементы: 1. W1 (Сеть)- выключатель сети. Нажатие этой клавиши вызывает включение питающего напряжения; 2. W2 (Сброс) – сброс измерителя. Нажатие этой клавиши вызывает сбрасывание схем секундомера FRM-16. 3. W3 (Пуск) –управление электромагнитом. Нажатие этой клавиши вызывает освобождение электромагнита и генерирование в схеме секундомера импульса как разрешение на измерения. ВЫПОЛНЕНИЕ РАБОТЫ Упражнение №1. Проверка закона сохранения импульса при неупругом центральном ударе. Определение коэффициента восстановления кинетической энергии. Для изучения неупругого удара берутся два стальных шара, но на одном шаре в месте, где происходит удар, прикрепляется кусочек пластилина. Таблица №1.
1. Получите у преподавателя начальное значение угла отклонения первого шара 2. Установите электромагнит так, чтобы угол отклонения первого шара (меньшей массы) соответствовал заданному значению 3. Отклоните первый шар на заданный угол, нажмите на клавишу <ПУСК> и произведити отсчет угла отклонения второго шара 4. Массы шаров 5. По формуле 6. По формуле 7. По формуле 8. По формуле 9. По формуле 10. По формуле 11. По формуле 12. Запишите интервал для импульса системы после столкновения в виде Найдите отношение проекции импульса системы после неупругого удара Упражнение №2. Проверка закона сохранения импульса и механической энергии при упругом центральном ударе. Определение силы взаимодействия шаров при столкновении.
Для изучения упругого удара берутся два стальных шара. Шар, который отклоняют к электромагниту, считается первым. Таблица №2.
1. Получите у преподавателя начальное значение угла отклонения первого шара 2. Установите электромагнит так, чтобы угол отклонения первого шара (меньшей массы) соответствовал заданному значению 3. Отклоните первый шар на заданный угол, нажмите на клавишу <ПУСК> и произведити отсчет углов отклонения первого шара 4. По формуле 5. По формуле 6. По формуле 7. По формуле 8. По формуле 9. По формуле 10. По формуле 11. По формуле 12. По формуле 13. По формуле 14. Запишите интервал для импульса системы после столкновения в виде 15. Запишите интервал для кинетической энергии системы после столкновения в виде Найдите отношение проекции импульса системы после упругого удара Найдите отношение кинетической энергии системы после упругого удара Сравните полученное значение величины силы взаимодействия КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Импульс и энергия, виды механической энергии. 2. Закон изменения импульса, закон сохранения импульса. Понятие о замкнутой механической системе. 3. Закон изменения полной механической энергии, закон сохранения полной механической энергии. 4. Консервативные и неконсервативные силы. 5. Удар, виды ударов. Запись законов сохранения для абсолютно упругого и абсолютно неупругого ударов. 6. Взаимопревращениемеханической энергии при свободном падении тела и упругих колебаниях.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 432; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.203.242 (0.01 с.) |










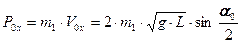 найдите импульс первого шара до столкновения и запишите в таблицу №1.
найдите импульс первого шара до столкновения и запишите в таблицу №1. найдите пять значений импульса системы шаров после столкновения и запишите в таблицу №1.
найдите пять значений импульса системы шаров после столкновения и запишите в таблицу №1. найдите среднее значение импульса системы после столкновения.
найдите среднее значение импульса системы после столкновения. найдите дисперсию среднего значения импульса системы шаров после столкновения. Найдите среднеквадратичное отклонение среднего значения
найдите дисперсию среднего значения импульса системы шаров после столкновения. Найдите среднеквадратичное отклонение среднего значения  импульса системы после столкновения. Полученное значение
импульса системы после столкновения. Полученное значение  найдите начальное значение кинетической энергии первого шара до столкновения
найдите начальное значение кинетической энергии первого шара до столкновения  найдите пять значений кинетической энергии системы шаров после столкновения
найдите пять значений кинетической энергии системы шаров после столкновения 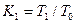 найдите коэффициент восстановления кинетической энергии
найдите коэффициент восстановления кинетической энергии  .
. . По полученному значению отношения проекции импульсов до и после столкновения сделайте вывод о сохранении импульса системы во время столкновения.
. По полученному значению отношения проекции импульсов до и после столкновения сделайте вывод о сохранении импульса системы во время столкновения.
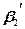


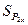


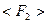
 найдите пять значений импульса системы шаров после столкновения и запишите в таблицу №2.
найдите пять значений импульса системы шаров после столкновения и запишите в таблицу №2. найдите среднее значение импульса системы после столкновения.
найдите среднее значение импульса системы после столкновения. найдите дисперсию среднего значения импульса системы шаров после столкновения. Найдите среднеквадратичное отклонение среднего значения
найдите дисперсию среднего значения импульса системы шаров после столкновения. Найдите среднеквадратичное отклонение среднего значения  занесите в таблицу №2.
занесите в таблицу №2. найдите пять значений кинетической энергии системы шаров после столкновения
найдите пять значений кинетической энергии системы шаров после столкновения  , и занесите их в таблицу №2.
, и занесите их в таблицу №2. найдите среднее значение кинетической энергии системы после столкновения.
найдите среднее значение кинетической энергии системы после столкновения. найдите дисперсию среднего значения кинетической энергии системы шаров после столкновения. Найдите среднеквадратичное отклонение среднего значения
найдите дисперсию среднего значения кинетической энергии системы шаров после столкновения. Найдите среднеквадратичное отклонение среднего значения  кинетической энергии системы после столкновения. Полученное значение
кинетической энергии системы после столкновения. Полученное значение  найдите коэффициент восстановления кинетической энергии
найдите коэффициент восстановления кинетической энергии 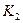 .
. найдите среднее значение силы взаимодействия
найдите среднее значение силы взаимодействия  .
. .
. . По полученному значению отношения кинетических энергий до и после столкновения сделайте вывод о сохранении механической энергии системы во время столкновения.
. По полученному значению отношения кинетических энергий до и после столкновения сделайте вывод о сохранении механической энергии системы во время столкновения. - кинетическая энергия материальной точки
- кинетическая энергия материальной точки - кинетическая энергия системы материальных точек.
- кинетическая энергия системы материальных точек.
 - Потенциальная энергия поднятой над Землёй системы материальных точек или протяжённого тела
- Потенциальная энергия поднятой над Землёй системы материальных точек или протяжённого тела , где к – коэффициент жёсткости пружины, Н/м
, где к – коэффициент жёсткости пружины, Н/м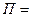 -
-  , где G – гравитационная постоянная,
, где G – гравитационная постоянная,
 , где η – величина безразмерная
, где η – величина безразмерная
 ,
, 
 ,
, 
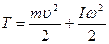 ,
, 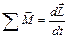

 ,
, ,
, 
 ,
,  ,
, 


