Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моменты количества движения точки относительно центра и оси.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для вычисления М. к. д. k материальной точки относительно центра О или оси z справедливы все формулы, приведённые для вычисления момента силы, если в них заменить вектор F вектором количества движения mv. Т. о., k o = [ r · mυ ], где r — радиус-вектор движущейся точки, проведённый из центра О, a kz равняется проекции вектора ko на ось z, проходящую через точку О. Изменение М. к. д. точки происходит под действием момента mo (F) приложенной силы и определяется теоремой об изменении М. к. д., выражаемой уравнением dko/dt = mo (F). Когда mо (F) = 0, что, например, имеет место для центральных сил, движение точки подчиняется Площадей закону. Главный М. к. д. (или кинетический момент) механической системы относительно центра О или оси z равен соответственно геометрической или алгебраической сумме М. к. д. всех точек системы относительно того же центра или оси, т. е. Ko = Σ koi, Kz = Σ kzi. Вектор Ko может быть определён его проекциями Kx, Ky, Kz на координатные оси. Для тела, вращающегося вокруг неподвижной оси z с угловой скоростью ω, K x = — I xzω, K y = — I yzω, K z = I zω, где lz — осевой, а Ixz, lyz — центробежные моменты инерции. Если ось z является главной осью инерции для начала координат О, то Ko = I zω. Изменение главного М. к. д. системы происходит под действием только внешних сил и зависит от их главного момента Moe. Эта зависимость определяется теоремой об изменении главного М. к. д. системы, выражаемой уравнением dKo/dt = Moe. Аналогичным уравнением связаны моменты Kz и Mze. Если Moe = 0 или Mze = 0, то соответственно Ko или Kz будут величинами постоянными, т. е. имеет место закон сохранения М. к. д.
Билет 20 Общее уравнение динамики. Общее уравнение динамики
Потенциальная сила. Работа потенциальной силы на конечном перемещении.
Потенциальная сила - сила, работа которой зависит только от начального и конечного положения точки её приложения и не зависит ни от вида траектории, ни от закона движения этой точки Работа потенциальной силы равна разности значений силовой функции в конечной и начальной точках пути и от вида траектории движущейся точки не зависит. Основным свойством потенциального силового поля и является то, что работа сил поля при движении в нем материальной точки зависит только от начального и конечного положений этой точки и ни от вида ее траектории, ни от закона движения не зависит.
Билет 21 Принцип виртуальных (возможных) перемещений. Существуют две различные формулировки принципа возможных перемещений. В одной формулировке утверждается, что для равновесия материальной системы необходимо, чтобы равнялась нулю сумма элементарных работ всех внешних сил, приложенных к системе, на любом возможном перемещении.
Мощность пары сил Парой сил называется система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на абсолютно твердое тело. Мощность пары сил:
где омега Z – проекция угловой скорости на ось вращения.
Билет 22 1.Прнцип виртуальных перемещений Если связь одна и описывается уравнением (2), физически ясно, что связь не нарушится, когда вектор виртуального перемещения
будет лежать в плоскости, касательной к поверхности связи, зафиксированной в данное мгновение времени. Математически это условие выражается как
где grad f - градиент функции (2) при фиксированном t, перпендикулярный поверхности связи в месте нахождения точки, равный
Учитывая выражения (3) и (5), раскрываем скалярное произведение в (4), получаем уравнение, которому должны удовлетворять проекции δxi, δyi, δzi виртуального перемещения δri, чтобы связь не нарушалась:
В вариационном исчислении бесконечно малые величины δri, δxi, δyi, δzi называются вариациями функций ri, xi, yi, zi. Изменения координат точек или уравнений связи при неизменном времени находятся синхронным варьированием, которое осуществляется согласно левым частям формул (4) и (6). То есть проекции δxi, δyi, δzi виртуального перемещения точки δr обращают в нуль первую вариацию уравнения связи при условии, что время не варьируется (синхронное варьирование):
Следовательно, виртуальное перемещение точки не характеризует ее движение, а определяет связь или, в общем случае, связи, наложенные на точку системы. Таким образом, виртуальные перемещения позволяют учесть эффект механических связей, не вводя реакции связей, как мы это делали раньше, и получать уравнения равновесия или движения системы в аналитическом виде, не содержащие неизвестных реакций связей. 2.Элементарная работа Элементарная работа силы равна скалярному произведению силы на дифференциал радиуса-вектора точки приложения силы. [ 2 ] Элементарная работа сил при этом зависит от выбора возможного перемещения системы. [ 3 ] Элементарная работа силы при вращении тела, на которое сила действуе
Билет 23 1. Принцип виртуальных перемещений в обобщенных координатах. Запишем принцип, выражая виртуальную работу активных сил системы в обобщенных координатах:
Так как на систему наложены голономные связи, вариации обобщенных координат не зависят между собой и не могут быть одновременно равны нулю. Поэтому последнее равенство выполнится только тогда, когда коэффициенты при δj (j = 1 ÷ s) одновременно обращаются в нуль, то есть
Таким образом, для равновесия материальной системы с голономными стационарными идеальными связями необходимо и достаточно, чтобы одновременно равнялись нулю все обобщенные силы системы по всем обобщенным координатам. Если силы, действующие на систему, являются потенциальными, то согласно (11) уравнения равновесия принимают вид
2.Работа силы на конечном перемещении
или
Билет 24 1.уравнение Лагранжа второго рода. Для вывода уравнений запишем принцип Даламбера-Лагранжа в обобщенных координатах в виде -Qju = Qj (j = 1 ÷ s). Принимая во внимание, что Фi = -miai = -midVi / dt, получаем:
Далее обобщенные силы инерции в левой части нужно выразить через кинетическую энергию(для систем с голономными связями обобщенные силы инерции равны):
Подставляя (2) в (1) получаем дифференциальное уравнение движения системы в обобщенных координатах, которое названо уравнением Лагранжа второго рода:
то есть, материальная система с голономными связями описывается уравнениями Лагранжа второго рода по всем s обобщенным координатам. Отметим важные особенности полученных уравнений. 1. Уравнения (3) - это система обыкновенных дифференциальных уравнений второго порядка относительно s неизвестных функций qj(t), полностью определяющих движение системы. 2. Число уравнений равно числу степеней свободы, то есть движение любой голономной системы описывается наименьшим числом уравнений. 3. В уравнения (3) не нужно включать реакции идеальных связей, что позволяет, находя закон движения несвободной системы, выбором обобщенных координат исключить задачу определения неизвестных реакций связей. 4. Уравнения Лагранжа второго рода позволяют указать единую последовательность действий для решения многих задач динамики, которую часто называют формализмом Лагранжа.
2. Условие относительного покоя материальной точки получают из динамического уравнения Кориолиса, подставив в это уравнение значения относительного ускорения и кориолисовой силы инерции равные нулю:
или
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 603; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.79.165 (0.009 с.) |

 – при движении системы с идеальными связями в каждый данный момент времен сумма элементарных работ всех приложенных активных сил и всех сил инерции на любом возможном перемещении системы будет равна нулю. Уравнение использует принцип возможных перемещений и принцип Даламбера и позволяет составить дифференциальные уравнения движения любой механической системы. Дает общий метод решения задач динамики. Последовательность составления: а) к каждому телу прикладывают действующие на него задаваемые силы, а также условно прикладывают силы и моменты пар сил инерции; б) сообщают системе возможные перемещения; в) составляют уравнения принципа возможных перемещений, считая систему находящейся в равновесии.
– при движении системы с идеальными связями в каждый данный момент времен сумма элементарных работ всех приложенных активных сил и всех сил инерции на любом возможном перемещении системы будет равна нулю. Уравнение использует принцип возможных перемещений и принцип Даламбера и позволяет составить дифференциальные уравнения движения любой механической системы. Дает общий метод решения задач динамики. Последовательность составления: а) к каждому телу прикладывают действующие на него задаваемые силы, а также условно прикладывают силы и моменты пар сил инерции; б) сообщают системе возможные перемещения; в) составляют уравнения принципа возможных перемещений, считая систему находящейся в равновесии. , (1)
, (1)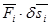 - скалярное произведение вектора силы
- скалярное произведение вектора силы  и вектора виртуального перемещения.
и вектора виртуального перемещения. 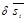
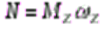 ,
,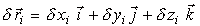
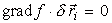
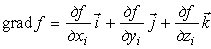

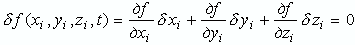

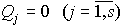

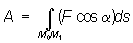

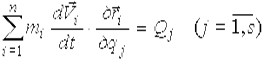 (1)
(1) (2)
(2) (3)
(3)