
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие о плоско параллельном движении твердого телаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В случае плоскопараллельного движения все точки тела, расположенные на прямой, перпендикулярной к определенной неподвижной плоскости I (рис.), совершают одинаковое движение. Поэтому изучение плоскопараллельного движения твердого тела может быть сведено к изучению движения плоской фигуры, образованной сечением тела плоскостью //, параллельной неподвижной плоскости /, при условии, что расстояние между плоскостями I u II постоянно (рис.).
Рассмотрим перемещение плоской фигуры на рис. из положения I в положение II. Положение плоской фигуры на (рис. a) определяется отрезком M1B1. Этот отрезок можно переместить из положения I в положение II следующим образом: перенести его параллельно самому себе в положение M2B/2 (при этом фигура совершит поступательное перемещение), а затем повернуть отрезок вокруг точки М2 против часовой стрелки на угол φ (фигура при этом совершит вращательное движение и займет положение II). Можно поступить иначе: сначала сообщить фигуре поступательное перемещение до положения отрезка В 2М /2, а затем повернуть вокруг точки В2 против часовой стрелки опять на угол φ.
Точку, вокруг которой фигура совершает поворот, называют полюсом. В первом случае полюсом была точка М2, во втором — В2. Очевидно, что за полюс может быть принята произвольная точка фигуры.
Рассматривая вращательную часть плоскопараллельного движения, нетрудно установить, что угол поворота не зависит от выбора полюса. Разложение плоскопараллельного движения можно использовать для определения скоростей точек тела. Так как плоскопараллельное движение фигуры может быть представлено как сумма двух движений — поступательного и вращательного, то скорость любой точки тела (рис. б) равна геометрической сумме: скорости vM движения полюса М и скорости вращательного движения vBM вокруг полюса М
vB = vM + vBM. Скорость вращательного движения определяется по формуле vBM = ω MB, где ω — угловая скорость вращения; MB — радиус вращения точки В относительного полюса М. Скорость вращательного движения vBM направлена перпендикулярно к радиусу вращения MB. Так как вращательная часть движения не зависит от выбора полюса, то угловая скоростью называется угловой скоростью плоской фигуры. В плоскости движущейся фигуры при плоскопараллельном движении в данный момент времени всегда есть точка, скорость которой равна нулю. Действительно, примем за полюс точку В (рис. в), восстановим из нее перпендикуляр к вектору скорости vB и отложим на этом перпендикуляре отрезок ВС = vB/ω в сторону, где относительные вращательные скорости направлены противоположно скорости выбранного полюса vB. Абсолютная скорость точки С определится как геометрическая сумма двух равных и противоположно направленных векторов: скорости поступательного движения vB и скорости вращательного движения vCB, причем vCB = ω ВС = ω * vB/ω= vB. Таким образом, абсолютная скорость точки С равна нулю. Эта точка С называется мгновенным центром скорости или мгновенным центром вращения плоской фигуры. Если эту точку С принять за полюс, то скорость произвольной точки М (рис. в) определится по формуле vm = vc + vMC, но vc = 0 и vM = vMC, или vM = ωМС, т. е. скорость любой точки плоской' фигуры определяется как вращательная относительно мгновенного центра скоростей. При определении мгновенного центра скоростей возможны следующие три случая: 1-й случай. Известны направления скоростей двух точек тела А и В. Мгновенный центр скоростей расположен на пересечении перпендикуляров, восставленных из точек к векторам их скоростей (рис. а).
2- й случай. При перекатывании тела без скольжения по неподвижной поверхности мгновенный центр скоростей находится в точке Р касания катящейся фигуры с поверхностью (рис. б). 3-й случай. Если скорости двух точек А и В параллельны между собой и одновременно перпендикулярны к линии, соединяющей эти точки, то мгновенный центр лежит на пересечении линий, соединяющих данные точки и концы их скоростей (рис. в, г).
и нормальное ускорение также не равно нулю ап = v 2/r ≠ 0 Следовательно, полное ускорение при неравномерном криволинейном движении складывается геометрически из касательного и нормального ускорений, т. е. a→ = at→ + an→ а = √аt2 + an2 Когда значение касательного ускорения постоянно (at = const), движение точки называется равнопеременным. Равнопеременное движение может быть равномерно-ускоренным и равномерно-замедленным, в зависимости от того, увеличивается или уменьшается численное значение скорости. Ускорения можно определить через значения скорости в начале и в конце произвольного промежутка времени аt = v – v0 / t откуда v = v0 + at t, При равномерно-ускоренном движении ускорение at считается положительным, а при равномерно-замедленном — отрицательным.
Примером равномерно-ускоренного движения может служить свободное падение тела. Ускорение свободного падения обозначается буквой g. Опытом установлено, что это ускорение составляет вблизи поверхности Земли в среднем 9,81 м/с2.
Раздел 3. Кинематика
Основные понятия
В кинематике изучается механическое движение материальных точек и твердых тел без учета причин, вызывающих эти движения. Кинематику часто называют геометрией движения. Механическое движение происходит в пространстве и во времени. Пространство, в котором происходит движение тел, рассматривается как трехмерное, все свойства его подчиняются системе аксиом и теорем эвклидовой геометрии. Время полагают ни с чем не связанным и протекающим равномерно. Современное развитие физики привело к иным представлениям о пространстве и времени. Теория относительности, созданная величайшим ученым современности Эйнштейном, показала, что при скоростях, близких к скорости света (300 000 км/с), пространство и время зависят от скорости движения. При обычных скоростях указанная зависимость практически не обнаруживается и представления о пространстве и времени, установленные в классической механике, сохраняют силу.
В природе не существует неподвижных тел и, следовательно, не может быть абсолютно неподвижных систем отсчета. Обычно условно неподвижной системой отсчета считают систему координатных осей, связанную с Землей. Рассмотрим для примера движение точки в какой-то условно неподвижной системе координат xyz (рис. 115). Положение точки М в пространстве определяется тремя координатами. Эти координаты изменяются при переходе точки в другое положение. Кривая, которую описывает точка при движении в пространстве относительно выбранной системы отсчета, называется ее траекторией.
Траектории делятся на прямолинейные (например, движение точек поршня двигателя) и криволинейные (круговые — движение точек шкива, круглой пилы; параболические — движение жидкости при истечении из отверстия в боковой стенке сосуда и др.). Движение точки в пространстве прежде всего определяется скоростью, котораяхарактеризует быстроту и направление движения точки в данный момент времени. В зависимости от скорости движение точки может быть равномерным и неравномерным. При равномерном движении скорость постоянна по величине, при неравномерном — переменна. Изменение скорости во времени характеризуется ускорением. Скорость и ускорение точки являются векторными величинами.
Уравнение движения точки В общем случае точка может двигаться по криволинейной траектории. Для изучения криволинейного движения точки необходимо уметь определить ее положение в назначенной системе отсчета (системе координат) в любой момент времени.
Уравнения, определяющие положение движущейся точки в зависимости от времени, называются уравнениями движения. В механики применяют два способа задания движения - естественный и координатный. -- Естественный способ задания движения точки. Положение точки на заданной траектории в любой момент времени однозначно определяется расстоянием s. Значит, если кроме траектории, на которой отмечено начало отсчета О, задана зависимость s = f(t) (1) между расстоянием s и временем t, то в любой момент времени можно точно определить положение точки на траектории. Уравнение 1 называется законом движения точки по заданной траектории. Пусть, например, задана некоторая траектория, движение точки по которой определяется уравнением s = 0,5t2(s - м, t - с): в момент времени t0 = 0 s0 = 0, т. е. точка находится вначале отсчета О; вмомент времени t1 = 1сточка находится на расстоянии s1 = 0,5 t12 = 0,5 * 12 = 0,5м; вмомент времени t2 = 2сточка находится на расстоянии s2 = 0,5 t22 = 0,5 * 22 = 2м от начала отсчета.
x = f1(t); y = f2(t). (2) Такой способ задания движения точки называется координатным. С помощью уравнений движения (2) можно найти траекторию точки, т. к. для каждого момента времени t можно вычислить координаты точки и следовательно указать ее положение
Скорость точки Рассмотрим некоторые основные определения, важные для последующего изложения. Если точка за равные промежутки времени проходит равные отрезки пути, то ее движение называется равномерным. Скорость равномерного движения v измеряется отношением пути s, пройденного точкой за некоторый промежуток времени, к величине этого промежутка времени v = s/t; м/с (4) 1 м/с за 1 час → 3600 м/час = 3,6 км/с т. е. 1 м/с = 3,6 км/ч 1 км/ч = 0,278 м/с [м/с] * 3,6 [км/ч]; [км/ч]: 3,6 [м/с] и нормальное ускорение также не равно нулю ап = v 2/r ≠ 0 Следовательно, полное ускорение при неравномерном криволинейном движении складывается геометрически из касательного и нормального ускорений, т. е. a→ = at→ + an→ а = √аt2 + an2 Когда значение касательного ускорения постоянно (at = const), движение точки называется равнопеременным. Равнопеременное движение может быть равномерно-ускоренным и равномерно-замедленным, в зависимости от того, увеличивается или уменьшается численное значение скорости. Ускорения можно определить через значения скорости в начале и в конце произвольного промежутка времени аt = v – v0 / t откуда v = v0 + at t, При равномерно-ускоренном движении ускорение at считается положительным, а при равномерно-замедленном — отрицательным.
Примером равномерно-ускоренного движения может служить свободное падение тела. Ускорение свободного падения обозначается буквой g. Опытом установлено, что это ускорение составляет вблизи поверхности Земли в среднем 9,81 м/с2.
Пример 1. Ускорение движения поезда, движущегося с уменьшением скорости, равно 0,16 м/с2. Определить время, за которое скорость поезда уменьшится с 50 до 25 км/ч Дано: a = - 0,16 v/c2 v0 = 50 км/ч = 50:3,6 = 13,9м/с v = 25км/ч = 25:3,6 = 6,9м/с Определить t Решение: v =v0 + at * t => t = v – v0 /at = 6,9 – 13,9 / - 0.16 = -7/ -0.16 = 43 c Пример 2. Водитель автомобиля движется со скоростью 72 км/ч увидел красный сигнал светофора начал торможение с ускорением 5 м/с2, на каком пути авто остановится.
Дано: v0 = 72 км/ч = 72:3.6 =20 м/c v1 = 0 at = -5м/с2 Определить S Решение: at = v – v0 /t => t = v – v0 / at = 0-20/ -5= 4c S = v0 + v/ 2* t = 20+0/ 2 * 4 = 40м Пример 3. Определить с какой высоты h нужно сбросить тяжелое тело без начальной скорости, чтобы к моменту падения на Землю скорость его достигла 49,05 м/с. Сопротивление воздуха пренебречь. Дано: v = 49,05 м/c V0 = 0 q = 9,81м/с2 Определить S
Пример 4. Камень упал в колодец. Через 4с был услышан плеск воды. Определить глубину колодца, считая, что звук распространяется мгновенно. Дано: t = 4c V0 = 0 q = 9,81м/с2 Определить S(h)
Ускорение точки При движении по криволинейной траектории скорость точки может изменяться и по направлению, и по величине. Изменение скорости в единицу времени определяется ускорением. Пусть точка М (рис. а) движется по какой-то криволинейной траектории и за время Δt переходит из положения М в положение M1. Расстояние, пройденное точкой, представляет собой дугу ММ1, ее длину обозначим Δs. В положении М точка имела скорость На рис. 119, а приращение скорости изображается вектором Скорость точки при перемещении ее из положения М в положение М1 изменилась и по величине, и по направлению. Среднее значение ускорения, характеризующего отмеченное изменение скорости, можно найти, разделив вектор приращения скорости
Переходя к пределу при Δt → 0, получим истинное ускорение точки как векторную производную от скорости
Найденное ускорение характеризует изменение численного значения скорости и ее направления. Для удобства ускорение раскладывают на взаимно перпендикулярные составляющие по касательной и нормали к траектории движения (рис. 119, б)
модуля скорости и соответственно определяется как производная от функции скорости at = Нормальная составляющая ап перпендикулярна к направлению скорости точки. Она определяет изменение направления вектора скорости. Численное значение нормального ускорения определяется по формуле ап = v2/r, где r — радиус кривизны траектории в рассматриваемой точке. Составляющие at и ап взаимно перпендикулярны, и поэтому значение полного ускорения определяется по формуле a =
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 1073; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.72.173 (0.014 с.) |

 Примером плоскопараллельного движения могут служить движение шатуна кривошипно-шатунного механизма, движение- колеса на прямолинейном участке пути и др.
Примером плоскопараллельного движения могут служить движение шатуна кривошипно-шатунного механизма, движение- колеса на прямолинейном участке пути и др. Итак, плоскопараллельное движение можно разложить на два составляющих движения: поступательное вместе с некоторым полюсом и вращательное вокруг этого полюса. Поступательная часть плоскопараллельного движения зависит от выбора полюса. Как видно из (рис. а,)поступательное перемещение M1M2 при выборе за полюс точки М2 не равно поступательному перемещению В1В2 при выборе за полюс точки В2.
Итак, плоскопараллельное движение можно разложить на два составляющих движения: поступательное вместе с некоторым полюсом и вращательное вокруг этого полюса. Поступательная часть плоскопараллельного движения зависит от выбора полюса. Как видно из (рис. а,)поступательное перемещение M1M2 при выборе за полюс точки М2 не равно поступательному перемещению В1В2 при выборе за полюс точки В2.


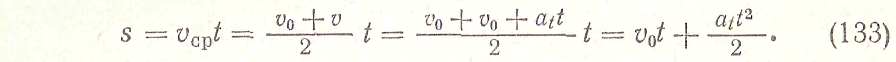 Перемещение точки при равнопеременном движении определяется по уравнению
Перемещение точки при равнопеременном движении определяется по уравнению 0
0






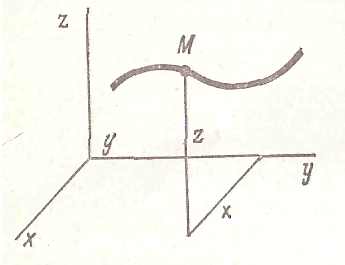 В общем случае различные точки твердого тела совершают разные движения. Поэтому и возникает необходимость изучить в первую очередь движение отдельных точек тела. Чтобы определить положение точки в пространстве, нужно иметь какое-то неподвижное тело или связанную с ним систему координатных осей, которую называют системой отсчета. Движение заданного тела или точки обнаруживается только путем сравнения с системой отсчета.
В общем случае различные точки твердого тела совершают разные движения. Поэтому и возникает необходимость изучить в первую очередь движение отдельных точек тела. Чтобы определить положение точки в пространстве, нужно иметь какое-то неподвижное тело или связанную с ним систему координатных осей, которую называют системой отсчета. Движение заданного тела или точки обнаруживается только путем сравнения с системой отсчета. -- Координатный способ задания движения точки. Положение движущейся в плоскости точки (рис. 116, б) можно определить, если известны ее координаты х и у относительно системы двух взаимно перпендикулярных координатных осей Ох и Оу. При движении точки ее координаты изменяются с течением времени, следовательно, х и у являются некоторыми функциями времени и определяют движение, точки:
-- Координатный способ задания движения точки. Положение движущейся в плоскости точки (рис. 116, б) можно определить, если известны ее координаты х и у относительно системы двух взаимно перпендикулярных координатных осей Ох и Оу. При движении точки ее координаты изменяются с течением времени, следовательно, х и у являются некоторыми функциями времени и определяют движение, точки: Пример 5. Поезд идет со скоростью 66 км/ч. На протяжении 800 м путь идет в гору, вследствие чего движение поезда становится равнозамедленным, и его скорость снижается до 50 км/ч. Определить величину ускорения (замедления) и время, затраченное на преодоление подъема.
Пример 5. Поезд идет со скоростью 66 км/ч. На протяжении 800 м путь идет в гору, вследствие чего движение поезда становится равнозамедленным, и его скорость снижается до 50 км/ч. Определить величину ускорения (замедления) и время, затраченное на преодоление подъема.
 , в положении М1 — скорость
, в положении М1 — скорость  .
.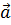 ср =
ср = 
 =
=  =
=  8
8 Касательная составляющая
Касательная составляющая 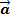 t совпадает по направлению со скоростью или противоположна ей. Она характеризует изменение
t совпадает по направлению со скоростью или противоположна ей. Она характеризует изменение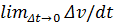 =dv/dt
=dv/dt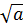 2t +a 2n
2t +a 2n


