
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод координат на плоскости и в пространстве.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Векторы и операция над ними Определение вектора Наиболее абстрактное понятие вектора будет введено в главе 16. Здесь же мы ограничимся определением, соответствующим наглядному представлению о векторе, известному из школьного курса математики. Определение 1 Вектором называется направленный отрезок. Таким образом, вектор - это отрезок, у которого выделен один конец, называемый концом вектора. Этот конец на рисунке обозначается стрелкой. Другой конец отрезка называется началом вектора. В математической литературе векторы обозначаются обычно одним из следующих способов:
Рис.1.Изображение векторов Определение 2. Два вектора называются равными, то есть не различаются как векторы, если соответствующие отрезки параллельны, имеют одинаковую длину и направление. Если считать, что на рисунке 1 векторы лежат в одной плоскости, тоа=с, то есть a и c -- разные обозначения одного и того же вектора. Векторы a и Определение 3 Векторы называются коллинеарными, если они параллельны одной прямой. Определение 4 Векторы называются компланарными, если они параллельны одной плоскости. Определение 5 Длиной или модулем вектора называется длина соответствующего направленного отрезка. Модуль вектора a обозначается К множеству векторов необходимо добавить еще один объект, который мы будем называть нулевым вектором. Его можно рассматривать как отрезок, у которого начало и конец совпадают. Длина такого вектора равна нулю, направления он не имеет. Все нулевые векторы равны друг другу. Так как нулевой вектор лежит на любой прямой, то, по определению, он считается коллинеарным любому вектору и перпендикулярным любому вектору.
В соответствии с принятыми выше обозначениями следовало бы нулевой вектор обозначать 0, но принято обозначать 0. По контексту всегда ясно, чем является 0, числом или вектором. Операции над векторами Определение 6 Суммой векторов a и b называется такой третий вектор c, что при совмещенных началах этих трех векторов, векторы a и b служат сторонами параллелограмма, а вектор c -- его диагональю (рис. 2).
Рис. 2.Сложение векторов Сложение векторов в соответствии с рисунком 2 называется сложением по правилу параллелограмма. Однако бывает более удобным использовать для сложения правило треугольника, которое становится ясным из рисунка 3. Из того же рисунка видно, что результаты сложения по правилу параллелограмма и по правилу треугольника одинаковы.
Рис. 3.Правило треугольника
Определение 7 Вектор b называется противоположным вектору a, если a и b коллинеарные, имеют противоположные направления и Определение 8 Разностью векторов a и b называется сумма Разность обозначается Определение 9 Произведением вектора a на вещественное число 1) 2) вектор b коллинеарен вектору a; 3) векторы b и a направлены одинаково, если Произведение вектора a на число
Рис. 4.Умножение вектора на число Рассмотрим некоторые свойства операций сложения и умножения вектора на число. Часть из них, которые будут особенно важны при обобщении понятия вектора, выделим в отдельную теорему. Теорема 1 Для любых векторов 1) 3) 4) 5) 6) 7) 8) Доказательство. Свойство 1 следует из того, что при сложении векторов по правилу параллелограмма (рис. 2) порядок слагаемых не влияет на построение параллелограмма. Доказательство свойства 2 следует из рисунка 5.
Рис. 5.Ассоциативность сложения
Свойства 3 и 4 очевидны при сложении векторов по правилу треугольника. Докажем свойство 5. Векторы, стоящие в обеих частях доказываемого равенства, имеют одинаковую длину
Свойство 6 очевидно, если
Рис.6.Свойство дистрибутивности
Случаи, когда Для доказательства свойства 7 заметим, что векторы Пусть Пусть Векторы f и g имеют одно направление. Оно совпадает с направлением a при Свойство 8 очевидным образом вытекает из определения 10.9 произведения вектора на число. Из свойства ассоциативности следует, что в сумме векторов, содержащей три и более слагаемых, можно скобки не ставить. Как найти сумму нескольких слагаемых, не используя попарных сумм, видно из рисунка 7.
Рис. 7.Сумма нескольких слагаемых Сформулируем еще несколько очевидных свойств операций сложения и умножения вектора на число: 9) равенство 10) вектор, противоположный вектору a, равен 11) для любых векторов a и b существует такой вектор x, что
Линии второго порядка. Линии второго порядка, плоские линии, декартовы прямоугольные координаты, которых удовлетворяют алгебраическому уравнению 2-й степени a11x2 + a12xy + a22y2 + 2a13x + 2a23y + a11 = 0. (*) Уравнение (*) может и не определять действительного геометрического образа, но для сохранения общности в таких случаях говорят, что оно определяет мнимую Л. в. п. В зависимости от значений коэффициентов общего уравнения (*) оно может быть преобразовано с помощью параллельного переноса начала и поворота системы координат на некоторый угол к одному из 9 приведённых ниже канонических видов, каждому из которых соответствует определённый класс линий. Именно, не распадающиеся линии:
y2 = 2px — параболы,
распадающиеся линии:
x2 - а2 = 0 — пары параллельных прямых, x2 + а2 = 0 — пары мнимых параллельных прямых, x2 = 0 — пары совпадающих параллельных прямых.
Поверхность второго порядка Пусть в пространстве задана прямоугольная декартова система координат. Поверхностью второго порядка называется поверхность, определяемая уравнением
где 1. Сфера Сферой называется геометрическое место точек пространства, равноудаленных от фиксированной точки, называемой центром. Теорема. Сфера радиуса
2. Эллипсоидом называется поверхность, каноническое уравнение которой имеет вид где
Рис. Эллипсоид 3. Однополостным гиперболоидом называется поверхность, каноническое уравнение которой имеет вид
Рис. Однополостный гиперболоид 5. Конусом второго порядка называется поверхность, уравнение которой в некоторой декартовой системе координат имеет вид
Рис. Изображение конуса с помощью сечений 6. Эллиптическим параболоидом называется поверхность, уравнение которой в некоторой декартовой системе координат имеет вид
Рис. Эллиптический параболоид
7. Цилиндрической поверхностью называется геометрическое место параллельных прямых, пересекающих данную линию. Эта линия называется направляющей, а параллельные прямые -- образующими. Рассмотрим уравнение вида и покажем, что оно определяет цилиндрическую поверхность с образующими, параллельными оси Заметим, что на плоскости Итак, делаем вывод, что если уравнение поверхности не содержит в явном виде какой-либо переменной, то это уравнение определяет в пространстве цилиндрическую поверхность с образующими, параллельными оси отсутствующего переменного и направляющей, которая в плоскости двух других переменных имеет то же самое уравнение. Поверхность, которая в некоторой декартовой системе координат задается уравнением
7. Преобразования плоскости и пространства. Отображение плоскости на себя Отображением плоскости на себя называется такое преобразование, что каждой точке исходной плоскости сопоставляется какая-то точка этой же плоскости, причем любая точка плоскости оказывается сопоставленой другой точке. Если при отображении плоскости на себя фигура F преобразовывается в фигуру F', то говорят, что фигура F' - образ фигуры F, а фигура F - прообраз фигуры F'. Если одним отображением фигура F переводится в фигуру F', а затем фигура F' переводится в фигуру F'', то отображение, переводящее F в F'' называется композицией двух отображений. Неподвижной точкой отображения называется такая точка A которая этим отображением переводится сама в себя. Отображение, все точки которого неподвижные называется тождественным отображением. Если при данном отображении разным точкам фигуры соответствуют разные образы, то такое отображение называется взаимно однозначным. Пусть фигура F' получена из фигуры F взаимно однозначным отображением f, то можно задать отображение обратное отображению f, которое определяется так: композиция отображения f и отображения, обратного f является тождественным отображением. Существует множество видов отображения плоскости на себя, рассмотрим некоторые из них:
1. Движения Параллельный перенос; Осевая симметрия; Поворот вокруг точки; Центральная симметрия 2. Подобие · Гомотетия Движение: Движением называется отображение плоскости на себя, при котором сохраняются все расстояния между точками. Движение имеет ряд важных свойств: 1. Три точки, лежащие на одной прямой, при движении переходят в три точки, лежащие на одной прямой, и три точки, не лежащие на одной прямой, переходят в три точки, не лежащие на одной прямой. 2. Отрезок движение переводится в отрезок. 3. При движении луч переходит в луч, прямая в прямую. 4. Треугольник движением переводится в треугольник. 5. Движение сохраняет величины углов. 6. При движении сохраняются площади многоугольных фигур. 7. Движение обратимо. Отображение, обратное движению является движением. 8. Композиция двух движений также является движением. Используя определение движения можно дать такое определение равенства фигур: Две фигуры называются равными, если одну из них можно перевести в другую некоторым движением. Виды движений: На плоскости существуют четыре типа движений: 1. Параллельный перенос. 2. Осевая симметрия 3. Поворот вокруг точки 4. Центральная симметрия Параллельный перенос: Параллельным переносом называется такое движение, при котором все точки плоскости перемещаются в одном и том же направлении на одинаковое расстояние. Осевая симметрия Точки X и X' называются симметричными относительно прямой a, и каждая из них симметричной другой, если a является серидинным перпендикуляром отрезка XX'. Каждая точка прямой a считается симметрична самой себе (относительно прямой a). Если дана прямая a, то каждой точке X соответствует единственная точка X', симметричная X относительно a. Симметрией плоскости относительно прямой a называется такое отображение, при котором каждой точке этой плоскости ставится в соответствие точка, симметричная ей относительно прямой a.
Поворот Поворот плоскости относительно центра O на данный угол Центральная симметрия: Центральная симметрия с центром в точке O это такое отображение плоскости, при котором любой точке X сопоставляется такая точка X', что точка O является серединой отрезка XX'. Однако можно заметить, что центральная симметрия является частным случаем поворота, а именно, поворота на 180 градусов. Действительно, пусть при центральной симметрии относительно точки O точка X перешла в X'. Тогда угол XOX'=180 градусов, как развернутый, и XO=OX', следовательно такое преобразование является поворотом на 180 градусов. Отсюда также следует, что центральная симметрия является движением. Центральная симметрия является движением, изменяющим направления на противоположные. То есть если при центральной симметрии относительно точки O точкам X и Y соответствуют точки X' и Y', то XY= - X'Y' Подобие: Подобием с коэффициентом k>0 называется отображение плоскости, при котором любым двумя точкам X и Y соответствуют такие точки X' и Y', что X'Y'=kXY. Отметим, что при k=1 подобие является движением, то есть движение есть частный случай подобия. Фигура F называется подобной фигуре F' с коэффициентом k, если существует подобие с коэффициентом k, переводящее F в F'. Простейшим, но важным примером подобия является гомотетия Гомотетия: Гомотетией с центром в точке O и коэффициентом k называется такое отображение плоскости, при котором каждой точке X сопоставляется такая точка X', что OX' = kOX, причем не исключается и возможность k<0. При k =-1 получается центральная симметрия с центром в точке O, при k =1 получается тождественное преобразование. Основное свойство гомотетии При гомотетии с коэффициентом k каждый вектор умножается на k. Подробнее: если точки A и B при гомотетии с коэффициентом k перешли в точки A' и B', то A'B' = kAB Доказательство. Пусть точка O - центр гомотетии. Тогда OA' = kOA, OB' = kOB. Поэтому A'B' = OB' - OA' = kOB - kOA = k(OB - OA) = kAB.(расставить векторы) Из равенства A'B' = kAB следует, что A'B' = |k|AB, то есть гомотетия с коэффициентом k является подобием с коэффициентом |k|. Отметим, что любое подобие с коэффициентом k можно представить в виде композиции гомотетии с коэффициентом k и движения. Некоторые свойства гомотетии 1.Гомотетия отрезок переводит в отрезок. 2.Гомотетия сохраняет величину углов. 3.. 4.Композиция двух гомотетий с общим центром и коэффициентами k1 и k2,будет гомотетией с тем же центром и коэффициентом Преобразование, обратное гомотетии с коэффициентом k будет гомотетией с тем же центром и коэффициентом 1/k.
8. Афинные п -мерные пространства Если в обычном трехмерном пространстве выбрана система координат Oxyz, то каждая точка
Любым двум точкам Пусть точка
В трехмерном пространстве уравнение
Если для векторов задано скалярное произведение формулой (18.3), то в аффинном пространстве можно определять расстояние между точками. Пусть
В соответствии с этим говорят, что уравнение
задает Можно рассматривать множество точек, задаваемых уравнением
9. Евкливоды п -мерные пространства Если координаты векторов
заданы в ортонормированном базисе, то скалярное произведение вычисляется по формуле
Аналогичной формулой можно задать и скалярное произведение в Пусть
Скалярное произведение векторов, обозначается оно обычно В отличие от обычного трехмерного пространства, где с помощью транспортира и линейки можно измерить угол между векторами и длину вектора, в Если
Предоставляем читателю самостоятельно убедиться в совпадении этой формулы с формулой (1) Вещественное линейное пространство, в котором задано скалярное произведение называется евклидовым пространством. В трехмерном пространстве модуль вектора равен корню квадратному из скалярного произведения вектора на себя
В трехмерном пространстве с помощью скалярного произведения определялся угол между векторами. В евклидовом пространстве тоже можно определить угол между векторами. Но угол в Два вектора евклидова пространства называются ортогональными, если их скалярное произведение равно нулю. Если
где черта над Комплексное линейное пространство, в котором введено скалярное произведение, называется унитарным пространством. В унитарном пространстве модуль вектора и условие ортогональности вводятся с помощью скалярного произведения так же, как в евклидовом пространстве. В координатной записи
Аксиоматический метод. Аксиоматический метод появился в Древней Греции, а сейчас применяется во всех теоретических науках, прежде всего в математике. Аксиоматический метод построения научной теории заключается в следующем: выделяются основные понятия, формулируются аксиомы теории, а все остальные утверждения выводятся логическим путём, опираясь на них. Основные понятия выделяются следующим образом. Известно, что одно понятие должно разъясняться с помощью других, которые, в свою очередь, тоже определяются с помощью каких-то известных понятий. Таким образом, мы приходим к элементарным понятиям, которые нельзя определить через другие. Эти понятия и называются основными. Когда мы доказываем утверждение, теорему, то опираемся на предпосылки, которые считаются уже доказанными. Но эти предпосылки тоже доказывались, их нужно было обосновать. В конце концов, мы приходим к недоказываемым утверждениям и принимаем их без доказательства. Эти утверждения называются аксиомами. Набор аксиом должен быть таким, чтобы, опираясь на него, можно было доказать дальнейшие утверждения. Выделив основные понятия и сформулировав аксиомы, далее мы выводим теоремы и другие понятия логическим путём. В этом и заключается логическое строение геометрии. Аксиомы и основные понятия составляют основания планиметрии. Так как нельзя дать единое определение основных понятий для всех геометрий, то основные понятия геометрии следует определить как объекты любой природы, удовлетворяющие аксиомам этой геометрии. Таким образом, при аксиоматическом построении геометрической системы мы исходим из некоторой системы аксиом, или аксиоматики. В этих аксиомах описываются свойства основных понятий геометрической системы, и мы можем представить основные понятия в виде объектов любой природы, которые обладают свойствами, указанными в аксиомах. После формулировки и доказательства первых геометрических утверждений становится возможным доказывать одни утверждения (теоремы) с помощью других. Доказательства многих теорем приписываются Пифагору и Демокриту. Гиппократу Хиосскому приписывается составление первого систематического курса геометрии, основанного на определениях и аксиомах. Этот курс и его последующие обработки назывались "Элементы".
Неевклидовы пространства. Неевклидовы геометрии, в буквальном понимании — все геометрические системы, отличные от геометрии Евклида; однако обычно термин «Н. г.» (Далее по тексту так будет обозначаться неевклидова геометрия) применяется лишь к геометрическим системам (отличным от геометрии Евклида), в которых определено движение фигур, причём с той же степенью свободы, что и в геометрии Евклида. Степень свободы движения фигур в евклидовой плоскости характеризуется тем, что каждая фигура без изменения расстояний между её точками может быть перемещена так, чтобы любая выбранная её точка заняла любое заранее назначенное положение; кроме того, каждая фигура может вращаться вокруг любой своей точки. В евклидовом трёхмерном пространстве каждая фигура может быть перемещена так, чтобы любая выбранная её точка заняла любое заранее назначенное положение; кроме того, каждая фигура может вращаться вокруг любой оси, проходящей через любую её точку. Среди Н. г. особое значение имеют Лобачевского геометрия и геометрия Римана, которые чаще всего и подразумевают, когда говорят о Н. г. Геометрия Лобачевского — первая геометрическая система, отличная от геометрии Евклида, и первая более общая теория (включающая евклидову геометрию как предельный случай). Геометрия Римана, открытая позднее, в некоторых отношениях противоположна геометрии Лобачевского, но вместе с тем служит ей необходимым дополнением. Совместное исследование геометрий Евклида, Лобачевского и Римана позволило в должной мере выяснить особенности каждой из них, а также их связи друг с другом и с другими геометрическими системами. Ниже обе Н. г. и геометрия Евклида сопоставляются как синтетические теории, затем в плане дифференциальной геометрии и, наконец, в виде проективных моделей. Н. г. как синтетические теории Геометрия Лобачевского строится на основе тех же аксиом, что и евклидова, за исключением только одной аксиомы о параллельных. Именно, согласно аксиоме о параллельных евклидовой геометрии, через точку, не лежащую на данной прямой а, проходит только одна прямая, которая лежит в одной плоскости с прямой а и не пересекает эту прямую; в геометрии Лобачевского принимается, что таких прямых несколько (затем доказывается, что их бесконечно много). В геометрии Римана принимается аксиома: каждая прямая, лежащая в одной плоскости с данной прямой, пересекает эту прямую. Эта аксиома противоречит системе аксиом евклидовой геометрии с исключением аксиомы о параллельных. Т. о., система аксиом, лежащая в основе геометрии Римана, необходимо должна отличаться от системы аксиом евклидовой геометрии не только заменой одной аксиомы о параллельных другим утверждением, но и в части остальных аксиом. Различными в этих геометриях являются аксиомы, которые служат для обоснования так называемых отношений порядка геометрических элементов. С
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 556; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.124.234 (0.018 с.) |

 . В двух последних случаях
. В двух последних случаях 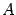 -- обозначение точки, являющейся началом вектора,
-- обозначение точки, являющейся началом вектора, 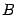 -- концом вектора. В тексте этого учебника будут использоватся первое и последнее из перечисленных обозначений.
-- концом вектора. В тексте этого учебника будут использоватся первое и последнее из перечисленных обозначений.
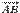 при равных длинах не равны друг другу, так как имеют разные направления. В соответствии с введенным равенством векторов слова "вектор параллелен прямой (плоскости)" и "вектор лежит на прямой (плоскости)" означают одно и то же, так как направленный отрезок можно передвинуть параллельно самому себе, вектор при этом не изменится.
при равных длинах не равны друг другу, так как имеют разные направления. В соответствии с введенным равенством векторов слова "вектор параллелен прямой (плоскости)" и "вектор лежит на прямой (плоскости)" означают одно и то же, так как направленный отрезок можно передвинуть параллельно самому себе, вектор при этом не изменится.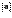 . Вектор a называется единичным, если
. Вектор a называется единичным, если  .
.

 . Вектор, противоположный вектору a, обозначается -а, то есть
. Вектор, противоположный вектору a, обозначается -а, то есть  .
. .
. , то есть
, то есть 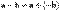 .
.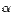 называется вектор b, определяемый условием
называется вектор b, определяемый условием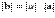 и, если
и, если  , то еще двумя условиями:
, то еще двумя условиями: , и противоположно, если
, и противоположно, если  .
. обозначается
обозначается  (рис 4).
(рис 4).
 и любых вещественных чисел
и любых вещественных чисел 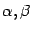 выполняются следующие свойства:
выполняются следующие свойства: (свойство коммутативности операции сложения);
(свойство коммутативности операции сложения);  (свойство ассоциативности операции сложения);
(свойство ассоциативности операции сложения); ;
; ;
; (свойство ассоциативности по отношению к числам);
(свойство ассоциативности по отношению к числам);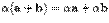 (свойство дистрибутивности по отношению к умножению на число);
(свойство дистрибутивности по отношению к умножению на число);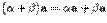 (свойство дистрибутивности по отношению к умножению на вектор;
(свойство дистрибутивности по отношению к умножению на вектор; .
.
 . Если это произведение равно нулю, то векторы в правой и левой частях доказываемого равенства нулевые и, следовательно, равны друг другу. В противном случае векторы
. Если это произведение равно нулю, то векторы в правой и левой частях доказываемого равенства нулевые и, следовательно, равны друг другу. В противном случае векторы  и
и  коллинеарны вектору a и имеют с ним одинаковое направление, если числа
коллинеарны вектору a и имеют с ним одинаковое направление, если числа 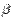 одного знака, и направление, противоположное вектору a, если
одного знака, и направление, противоположное вектору a, если  разного знака. Следовательно,
разного знака. Следовательно,  .
. . Если
. Если  и векторы a и b неколлинеарны, то это свойство вытекает из подобия треугольников на рисунке 6.
и векторы a и b неколлинеарны, то это свойство вытекает из подобия треугольников на рисунке 6.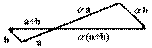
 или a и b коллинеарны, предоставляем проанализировать читателю самостоятельно.
или a и b коллинеарны, предоставляем проанализировать читателю самостоятельно. и
и 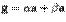 коллинеарны. Без ограничения общности можно считать, что
коллинеарны. Без ограничения общности можно считать, что  (в противном случае поменяем местами
(в противном случае поменяем местами  ,
,  .
. ,
,  . Получили, что
. Получили, что  в обоих случаях.
в обоих случаях. . Следовательно,
. Следовательно,  . Свойство 7 доказано.
. Свойство 7 доказано.
 верно тогда и только тогда, когда или
верно тогда и только тогда, когда или  , или
, или 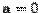 ;
;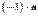 , то есть
, то есть  ;
; — эллипсы,
— эллипсы, — гиперболы,
— гиперболы, — мнимые эллипсы;
— мнимые эллипсы; — пары пересекающихся прямых,
— пары пересекающихся прямых, — пары мнимых пересекающихся прямых,
— пары мнимых пересекающихся прямых, (1)
(1) - вещественные числа, причем хотя бы одно из чисел
- вещественные числа, причем хотя бы одно из чисел  отлично от нуля.
отлично от нуля. с центром в точке
с центром в точке  имеет уравнение
имеет уравнение 

 ,
, 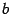 ,
,  -- положительные числа.
-- положительные числа.
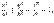 где
где 
 где
где 
 где
где 

 . Пусть
. Пусть  -- некоторая точка, координаты которой удовлетворяют уравнению. Поскольку в это уравнение не входит явно переменная
-- некоторая точка, координаты которой удовлетворяют уравнению. Поскольку в это уравнение не входит явно переменная  , ему будут удовлетворять координаты всех точек
, ему будут удовлетворять координаты всех точек 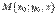 , где
, где  лежит на поверхности, определяемой уравнением. Отсюда следует, что на поверхности целиком лежит прямая, проходящая через точку
лежит на поверхности, определяемой уравнением. Отсюда следует, что на поверхности целиком лежит прямая, проходящая через точку  параллельно оси
параллельно оси  уравнение определяет направляющую рассматриваемой цилиндрической поверхности.
уравнение определяет направляющую рассматриваемой цилиндрической поверхности. называется эллиптическим цилиндром, поверхность, которая задается уравнением
называется эллиптическим цилиндром, поверхность, которая задается уравнением 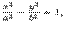 называется гиперболическим цилиндром, а которая задается уравнением
называется гиперболическим цилиндром, а которая задается уравнением 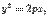 называется параболическим цилиндром.
называется параболическим цилиндром. (
( ) в данном направлении определяется так: каждой точке X плоскости ставится в соответствие такая точка X', что, во-первых, OX'=OX, во-вторых
) в данном направлении определяется так: каждой точке X плоскости ставится в соответствие такая точка X', что, во-первых, OX'=OX, во-вторых  и, в-третьих, луч OX' откладывается от луча OX в заданном направлении. Точка O называется центром поворота, а угол
и, в-третьих, луч OX' откладывается от луча OX в заданном направлении. Точка O называется центром поворота, а угол  -углом поворота.
-углом поворота.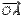 . Аналогично мы можем считать, что набор из
. Аналогично мы можем считать, что набор из 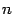 чисел является точкой
чисел является точкой 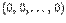 . За единичные векторы на осях координат в этом случае принимаются радиус-векторы точек
. За единичные векторы на осях координат в этом случае принимаются радиус-векторы точек
 из
из  нужно из координат конца вектора вычесть координаты начала.
нужно из координат конца вектора вычесть координаты начала. , являющаяся началом новой системы координат, имеет координаты
, являющаяся началом новой системы координат, имеет координаты  . Пусть
. Пусть  в старой системе координат и
в старой системе координат и  в новой системе координат. Тогда связь между старыми и новыми координатами задается формулами
в новой системе координат. Тогда связь между старыми и новыми координатами задается формулами
 задает плоскость. Аналогично в
задает плоскость. Аналогично в  где
где  -- числа, задает плоскость размерности
-- числа, задает плоскость размерности  , обычно ее называют гиперплоскостью. В трехмерном пространстве система из двух уравнений задает прямую. В
, обычно ее называют гиперплоскостью. В трехмерном пространстве система из двух уравнений задает прямую. В  из
из  уравнений,
уравнений,  , задает плоскость размерности
, задает плоскость размерности  , если ранг матрицы системы равен
, если ранг матрицы системы равен 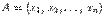 ,
,  -- точки пространства, тогда расстояние между ними
-- точки пространства, тогда расстояние между ними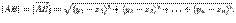
 задает в
задает в  -мерную сферу, а неравенство
-мерную сферу, а неравенство
 . При некоторых ограничениях на функцию
. При некоторых ограничениях на функцию  , это уравнение будет определять
, это уравнение будет определять  -мерную поверхность (гиперповерхность), а неравенство
-мерную поверхность (гиперповерхность), а неравенство  -- область в
-- область в  и
и 

 -- вещественное
-- вещественное  . Тогда векторы
. Тогда векторы 
 , задается формулой
, задается формулой  (1)
(1)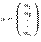 ,
,  -- координатные столбцы векторов
-- координатные столбцы векторов 
 . В евклидовом пространстве модуль вектора определим аналогично
. В евклидовом пространстве модуль вектора определим аналогично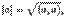 то есть
то есть 

 означает комплексное сопряжение.
означает комплексное сопряжение.



