
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проективные пространства и их модели. Проективные координаты.Содержание книги
Поиск на нашем сайте
Проективное над телом K — пространство состоящее из прямых (одномерных подпространств) некоторого линейного пространства L(K) данным телом. Данные прямые называются точками проективного пространства. Если L имеет размерность n + 1, то размерностью проективного пространства называется число n а само проективное пространство обозначается KPn и называется ассоциированным с L (чтобы это указать, принято обозначение P(L)). Точки KPn можно описывать с помощью однородных координат. Проективное пространство может быть также определено системой аксиом типа гильбертовской, что наиболее интересно в случае проективной плоскости. Тогда оказывается, что проективная плоскость, определённая аксиомами может быть определена как двухмерное проективное пространство над некоторым телом тогда и только тогда, когда выполняется т. н. аксиома Дезарга, которая для размерностей больших 2 является теоремой. Пусть M есть гиперплоскость в линейном пространстве L. Проективное пространство Свойства На дополнении проективной гиперплоскости Обратно, взяв за основу аффинное пространство A, можем получить проективное пространство как аффинное, к которому добавлены бесконечно удалённые точки. Первоначально проективное пространство и было введено таким образом. Проективные координаты — взаимно однозначное соответствие между элементами n-мерного проективного пространства KPn над телом K и классами эквивалентности упорядоченных конечных подмножеств элементов тела K. Пусть в совокупности строк (x0,x1,...,xn) не равных одновременно нулю элементов тела K введено отношение эквивалентности слева (справа): (x0,x1,...,xn)˜(y0,y1,...,yn), если существует
Тогда совокупность классов эквивалентности находится во взаимно однозначном соответствии с совокупностью точек проективного пространства KPn. 12. Проективные преобразования и их группы. Проективное преобразование, взаимно однозначное отображение проективной плоскости или проективного пространства в себя, при котором точки, лежащие на прямой, переходят в точки, также лежащие на прямой (поэтому П. п. иногда называется коллинеацией). П. п. проективной прямой называется взаимно однозначное отображение её в себя, при котором сохраняется гармоническое расположение точек этой прямой. Простейшим и вместе с тем наиболее важным для приложений примером П. п. является гомология — П. п., оставляющее на месте прямую и точку вне её. Примером П. п. пространства является перспектива, т. е. проектирование фигуры F, лежащей в плоскости П, из точки S в фигуру F', расположенную в плоскости П', любое П. п. получается конечной последовательностью перспектив. П. п. образуют группу, основным инвариантом которой является двойное отношение четырёх точек прямой. Теории инвариантов групп П. п., оставляющих на месте некоторую фигуру, представляют собой метрические геометрии (см. Проективная метрика). Основная теорема о П. п. проективной плоскости состоит в том, что каковы бы ни были четыре точки А, В, С, D плоскости П, из которых никакие три не лежат на одной прямой, и четыре точки A', B', C', D' той же плоскости, из которых никакие три также не лежат на одной прямой, существует и притом только одно П. п., которое точки А, В, С, D переводит соответственно в точки A', B', C', D'. Эта теорема применяется в номографии и аэрофотосъёмке. Аналогичная теорема имеет место и в проективном пространстве: там П. п. определяется пятью точками, из которых никакие четыре не лежат в одной плоскости. Эта теорема эквивалентна аксиоме Паппа. В однородных координатах П. п. выражается однородным линейным преобразованием, определитель матрицы которого не равен нулю. Рассматриваются также П. п. евклидовой плоскости или пространства; в декартовых координатах они выражаются дробно-линейными функциями, причём свойство взаимной однозначности утрачивается.
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 325; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.147.146 (0.006 с.) |

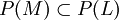 называется проективной гиперплоскостью P(L).
называется проективной гиперплоскостью P(L). существует естественная структура аффинного пространства.
существует естественная структура аффинного пространства.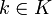 такой, что
такой, что



