Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Параграф 4. Аффинные подпространства и r-мерные плоскости в аффинном пространстве.Содержание книги
Поиск на нашем сайте
Пусть дано ЛВП размерности n(dimV=n) Рассмотрим произвольную систему линейных однородных уравнений от n переменных. Пусть ее ранг равен r. Теорема (о подпространствах порожденных слоу): Совокупность всех решений СЛОУ образует линейное векторное подпространство размерностью n-r в ЛВП порожденного фундаментальной системой решений СЛОУ Аффинные пространства: В классическом определении ЛВП можно считать, что его элементами являются n-мерные точки. Расширим понятие ЛВП, добавив к его элементам понятие геометрического вектора, тем самым получим понятие точечно-векторного или аффинного пространства. Пусть имеется ЛВП, элементами которого являются точки. Каждым любым двум точкам этого пространства однозначным образом сопоставим единственную упорядоченную пару этих точек, которую в дальнейшем будем называть геометрическим вектором(вектором).
Точки и вектора в получившемся аффинном пространстве обладают следующими свойствами (аксиомы аффинного пространства): 1) Для каждой точки М и каждого вектора х существует точка N такая, что
2) Для любых точек M,N и P выполнимо равенство: 3) Совокупность всех точек ЛВП пополненная векторами, удовлетворяющих аксиомам, называют точечно- векторным или аффинным пространством. Аффинное пространство является n-мерным, если соответствующие ЛВП так же являются n- мерными. Предложение(О простейших свойствах векторов аффинного пространства): 1) Если 2) Вектор, у которого начало и конец совпадают, являются нулевым вектором n- мерного аффинного пространства. Это следует из равенства 3) Для каждого вектора существует противоположный у нему вектор. Это следует из равенства: Пусть задана т. О (начало координат) и система базисных векторов приложенных к точке О. Согласно понятию ЛВП вектор х есть В случае когда заданы произвольные 2 точки.
Действительно, рассмотрим равенство:
Что и требовалось доказать. Теорема о изоморфизме аффинных пространств: Естественным образом возникает вопрос, будут ли изоморфными 2 аффинных пространства в случае когда изоморфными являются соответствующие лвп. Утвердительный ответ дается в Теореме (об изоморфизме аффинных пространств): Любые два изоморфных аффинных пространства имеют одинаковую размерность (т.е они изоморфны только в этом случае) Доказательство: A и A’ называют изоморфными, если существует взаимно-однозначное отображение такое, что выполнены свойства: 1) Остальные свойства те же, что и свойства в определении изоморфизма ЛВП. Выберем в каждом из А и А’ две точки такие, что координаты их будут равны, тогда имеет место следующее:
Переход от базиса к базису в аффинном пространстве: Случай 1: Переход от базиса к базису имеющих общую точку приложения: В данном случае переход осуществляется с помощью матрицы перехода, составленной из координат нового базиса. Преобразование координат вектора при таком переходе осуществляется с помощью известных алгебраических действий. Случай 2: Переход от базиса к базису с изменением точки приложения базисных векторов. Дальнейшие рассуждения базируются на равенстве Координаты вектора при переходе от старого базиса к новому изменяются в соответствии с известными алгебраическими действиями с учетом вычитания вектора соединяющего точки приложения базисного векторов.
Линейное многообразие Пусть дано n- мерное ЛВП
И ей дана присоединенная (соответствующая) система линейных уравнений(**) Будем считать, что каждая система (*) и (**) имеет ранг основной матрицы, равный r и введем обозначение s=n-r. Совокупность всех решений системы (*) (точек ЛВП Согласно теореме о решениях системы СЛНУ и присоединенной системы СЛОУ можно сказать что линейное многообразие представляет собой множество \совокупность всех решений системы (**), к каждому из которых прибавлено некоторое частное решение системы (*)
Таким образом второе определение линейного многообразия имеет вид:
Можно считать, что совокупность решений (**) представляет собой некоторую плоскость в n- мерном пространстве Пусть ко всем векторам этой плоскости прибавлен некоторый произвольный вектор а из пространства Плоскость П будет собой представлять плоскость П(0) сдвинутую на вектор а. Концы всех векторов полученных путем сложения векторов плоскости П(0) и фиксированного вектора а, представляет собой плоскость П, и каждый из них согласно вышеуказанной теореме о связи решений, совокупность всех решений системы (*). Верно и обратное: Пусть дана система (**) (Плоскость П(0)), и некоторый произвольный вектор А из пространства
В силу произвольности выбора вектора А, легко понять, что вектор А не единственный и система (***) представляет собой систему (*). Таким образом, множество всех решений системы (*) (плоскость П) представляет собой множество всех решений системы (**) (Плоскость П(0)), к каждому из которых прибавлен произвольный фиксированный вектор А, имеющий собой некоторое частное решение системы (*). Линейное многообразие (*) называется s-мерным если пространство порожденное системой так же является s- мерным. S- мерыне плоскости в аффинном пространстве. Пусть дано аффинное пространство Вновь рассмотрим систему (*) и на этой основе «родим» следующее определение: Множество\совокупность всех точек из аффинного пространства Одномерные плоскостью. Называются прямыми. Плоскости размерность которых больше 1 и меньше n называются гиперплоскостями. Всякую гиперплоскость можно задать системой линейных неоднородных уравнений вида (*). Например гиперплоскость размерности n-1 можно задать с помощью одного уравнения (s=n-r=n-n+1=1):
Легко показать, что при переходе от одного начала координат к другому в аффинном пространстве Пусть П – некоторая s- мерная плоскость, удовлетворяющая системе (*). П(0) – такая же s- мерная плоскость, проходящая через начало координат. Если ко всеем векторам П(0) прибавить произвольный вектор А из Две S- мерные гиперплоскости параллельны, если определяющие их системы вида (*) таковы, что присоединенные системы являются равносильными. То есть имеют одни и те же решения. Две s- мерные гиперплоскости называются пересекающимися, если определяющие их системы вида (*) таковы, что присоединенные системы имеют общее решение, которое составлено из уравнений присоединенных систем. S- мерная плоскость = П(0) и N – Мерная гиперплоскость = П(1) называются параллельными, если гиперплоскость П(0) параллельная любой гиперплоскости содержащейся в гиперплоскости П(1). Другими словами, всякое решение присоединенной системы характеризующей гиперплоскость П(1), является решением присоединенной системы, характеризующей гиперплоскость П(0). То есть, иначе говоря, СЛОУ, характеризующая гиперплоскость П(1), является следствием СЛОУ, характеризующей П(0) Пусть П – s- мерная гиперплоскость. Общее решение присоединенной системы, характеризующей гиперплоскость п(системы (*)и (**)), имеет вид
Или
Переходя к координатной записи, получаем параметрическое задание плоскости П:
Примечание: 1) Если гиперплоскость П оказалась прямой, то фундаментальное решение системы (**) будет единственным, и вследствие этого константа а будет иметь единственное значение. Исключая параметр «а» из системы (****) получаем каноническое уравнение прямой. (учим геометрию господа) 2) Если гиперплоскость П оказалась двухмерной плоскостью, то (система (****)) будет иметь два фундаментальных решения системы (**). Следовательно, будет 2 параметра: «а1» и «а2». Тогда система (****) будет иметь вид:
S- мерная плоскость = П(0) и N – Мерная гиперплоскость = П(1) называются пересекающимися если, СЛНУ (*), составленная из СЛНУ, задающих эти гиперплоскости, имеет решение.
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 418; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.124.23 (0.006 с.) |

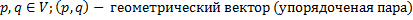
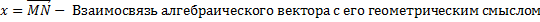
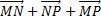
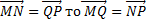 . Данное свойство непосредственно следует из равенства
. Данное свойство непосредственно следует из равенства 


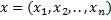 . То по аксиоме 1.АП (Аффинных пространств) имеет место следующее OX=X и
. То по аксиоме 1.АП (Аффинных пространств) имеет место следующее OX=X и  . Координатами вектора в АП считают координаты соответствующего алгебраического вектора
. Координатами вектора в АП считают координаты соответствующего алгебраического вектора , то
, то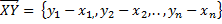
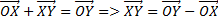
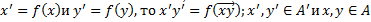

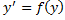
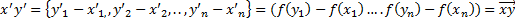
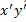 является образом
является образом 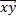 при изоморфизме, что можно установить, пользуясь понятием изоморфизма между ЛВП и его простейшими свойствами.(все тоже самое что и выше, только в обратном порядке)
при изоморфизме, что можно установить, пользуясь понятием изоморфизма между ЛВП и его простейшими свойствами.(все тоже самое что и выше, только в обратном порядке)
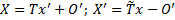
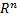 , над множеством R(или С), и дана система линейных неоднородных уравнений (*)
, над множеством R(или С), и дана система линейных неоднородных уравнений (*)
 – алгебраический вектор, равный суме всех фундаментальных решений системы (*) с некоторыми скалярами; частное решение систем (*) обозначим через а, и обозначим через х общее решение системы (*)
– алгебраический вектор, равный суме всех фундаментальных решений системы (*) с некоторыми скалярами; частное решение систем (*) обозначим через а, и обозначим через х общее решение системы (*)

 размерности n в котором выбрано некоторое начало координат.
размерности n в котором выбрано некоторое начало координат.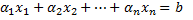
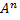 ранг системы (*) не уменьшается.
ранг системы (*) не уменьшается.