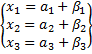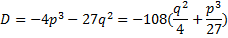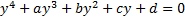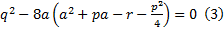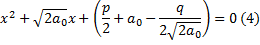Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Параграф 5. Количество корней многочленаСодержание книги
Поиск на нашем сайте Пусть дан полином с действительными коэффициентами. Для оценки количества корней используется система Штурма и система производных. Система Штурма: Данная система применяется для многочленов с действительными коэффициентами в предположении, что он не имеет кратных корней. Система полиномов f(0),f(1),…f(k) (*) называется системой Штурма, если выполнены следующие условия: 1) Соседние полиномы в наборе (*) не должны иметь общих корней. 2) Последний полином f(k) не должен иметь корней (т.е должен быть полиномом нулевой степени. Константой) 3) Пусть a- действительный корень f(i), i=2,k-1 и для этого корня многочлены Пусть С не является корнем полинома f. Используя данное число определяется величина w(c), которая называется количеством перемен знаков в системе Штурма. Теорема Штура: Если действительные числа а и в(a<b) не являются корнями полинома f, не имеющего кратных корней, то имеет место Где М – количество действительных корней полинома f заключены между а и в. Теорема о существовании системы Штурма: Всякий многочлен с действительными коэффициентами и не имеющих корней обладает системой Штурма. Примечание (К теореме Штурма): Если переменная x подходит через корень многочлена f, то величина w(x) изменяет свое значение ровно на единицу (в меньшую сторону). Практический метод построения системы Штурма: 1) В качестве f(0) выбираем исходный полином. 2) F(1) – первая производная исходного полинома 3) Остаток от деления шага 1 на шаг 2 с противоположным знаком. (ывполняемо для последующих шагов) Пусть дан многочлен ненулевой степени n. Рассмотрим производные данного многочлена, начиная от нулевой производной и заканчивая n-1 (константа).(*) Для определения количества корней заключенных между a и b можно воспользоваться теоремой Штурма. НО! Недостатком этого подхода будет является предположении об отсутствии кратных корней. Так же подсчитывается количество перемен знаков в системе (*) Рассмотрим число С (С принадлежит (a;b)) которое НЕ является корнем многочлена f, но оно может оказаться корнем каких-либо многочленов из системы (*), тоесть имеет место следующее:
Но при этом число C Не является корнем
Введем следующие функции подсчета числа перемен знаков в системе (*):
Примечание к знаку числа Знак многочлена в пункте (а), равных нулю, считается равным знаку последнего ненулевого числа Теорема Бюдана-Фурье: Если действительные числа а и в не являются корнями многочлена f(x) с действительными коэффициентами, то количество действительных корней заключенных между а и в равно разности Теорема Декарта: Число положительных корней многочлена f(x) подсчитываемых столько раз, какова их кратность, равна числу количества перемен знаков в системе коэффициентов или меньше этого количества на четное число. Обобщенная теорема Виетта:
И так далее по аналогии. Интерполяционный многочлен Лагранжа:
Эта формула позволяет построить многочлен степени не ниже k, по заранее заданным k переменных (их значениям) и собственным значениям функции в этих точках. Вычисления корней кубических многочленов: Пусть дано кубическое уравнение вида (в приведенной форме):
Производится подстановка вида И уравнение сводится к виду: Формулы Кардано:
Для получения корней кубического уравнения можно найти соответствующие значения выражений а и в, но их нельзя комбинировать в произвольном порядке. Пусть а(1) один из корней выражения «альфа». Оставшиеся а2 и а3 находим по правилам: А2=а1*е А3=а1*е^2, где е – первообразный кубический корень из …(Какой то хрени. Не могу понять) Аналогичным образом считаем значения Таким образом корни кубического уравнения могут быть найдены по формулам:
Заведем понятие дискриминанта для кубического уравнения с действительными коэффициентами:
Если D>0 то уравнение имеет 3 действительных корня. D<0 уравнение имеет 1 действительных и 2 комплексно сопряженных. D=0 уравнение имеет 3 действительны корня, 2 из которых кратные(одинаковые) Уравнения четвертой степени:
Производится подстановка вида И уравнение сводится к виду Для решения уравнения (2) будем использовать корни дополнительного уравнения, через которые будут выражены корни исходного уравнения. Дополнительное уравнение: Уравнение 3 является кубическим уравнением, зависящем от неизвестной а, корни данного уравнения находятся с помощью формулы кордано. И пусть например а(0) – один из корней уравнения (3) Используя корень a(0) решаем систему уравнений:
Решая каждое уравнение систему (4) получаем корни исходного уравнения.
|
||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1980; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.008 с.) |

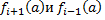 должны иметь разные знаки.
должны иметь разные знаки.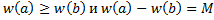

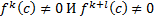
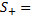 Значение перемен знаков с учетом пунктов (а) и (в)
Значение перемен знаков с учетом пунктов (а) и (в)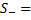 значению перемен знаков; Считается, что знак с учетом пунктов (а) и (в) знак равен знаку
значению перемен знаков; Считается, что знак с учетом пунктов (а) и (в) знак равен знаку 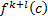 если разность l-I (i=0,l-1) при подсчете производных
если разность l-I (i=0,l-1) при подсчете производных 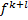 является четной, и будет иметь противоположный знак, если разность не четная. (Вобще не понял что написано, но пярм так и сказано)
является четной, и будет иметь противоположный знак, если разность не четная. (Вобще не понял что написано, но пярм так и сказано)
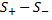 если меньше этой разности на четное число, при условии подсчета кратности корней f(x)
если меньше этой разности на четное число, при условии подсчета кратности корней f(x)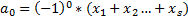
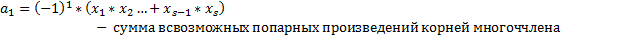
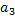 -аналогично а1 только по три, а не по 2.
-аналогично а1 только по три, а не по 2.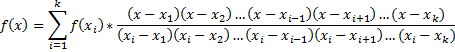
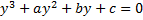
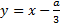
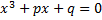
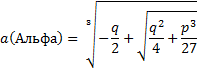
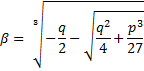
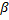 .
.